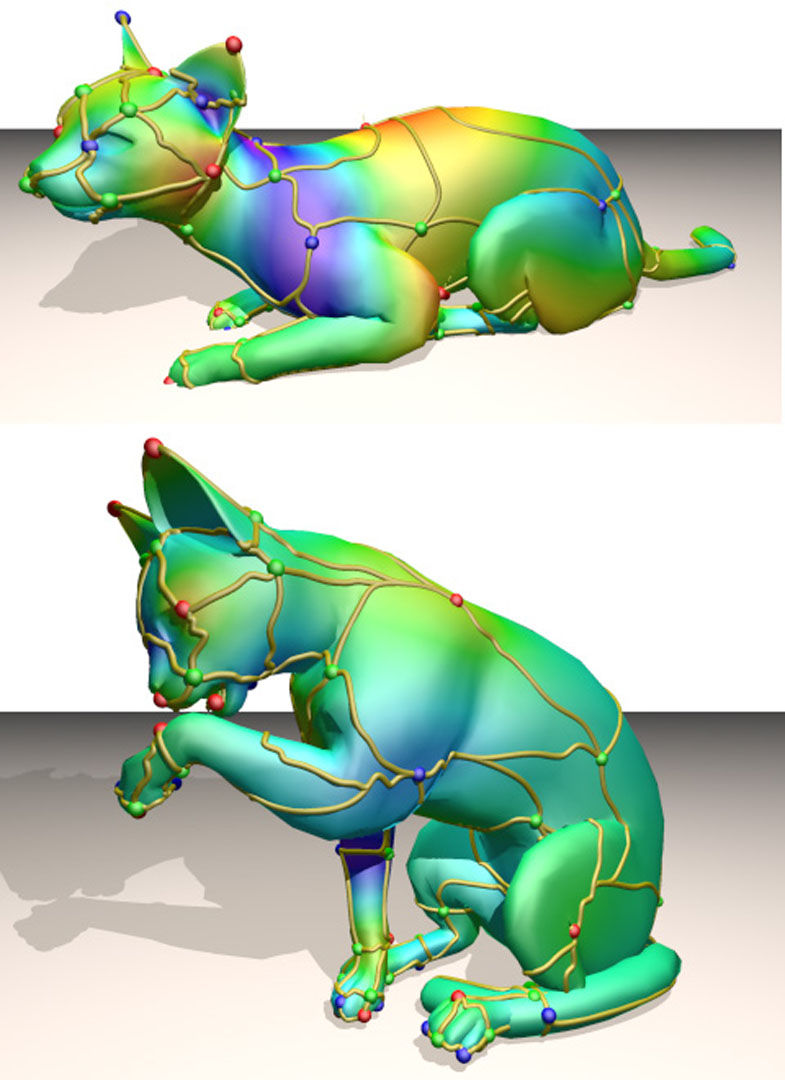
“Spectral surface quadrangulation” by Dong, Bremer, Garland, Pascucci and Hart

Resampling raw surface meshes is one of the most fundamental operations used by nearly all digital geometry processing systems. The vast majority of this work has focused on triangular remeshing, yet quadrilateral meshes are preferred for many surface PDE problems, especially fluid dynamics, and are best suited for defining Catmull-Clark subdivision surfaces. We describe a fundamentally new approach to the quadrangulation of manifold polygon meshes using Laplacian eigenfunctions, the natural harmonics of the surface. These surface functions distribute their extrema evenly across a mesh, which connect via gradient flow into a quadrangular base mesh. An iterative relaxation algorithm simultaneously refines this initial complex to produce a globally smooth parameterization of the surface. From this, we can construct a well-shaped quadrilateral mesh with very few extraordinary vertices. The quality of this mesh relies on the initial choice of eigenfunction, for which we describe algorithms and hueristics to efficiently and effectively select the harmonic most appropriate for the intended application.

1. Alliez, P., Cohen-Steiner, D., Devillers, O., Lévy, B., and Desbrun, M. 2003. Anisotropic polygonal remeshing. TOG 22, 3, 485–493. (Proc. SIGGRAPH).]] Google ScholarDigital Library
2. Alliez, P., Ucelli, G., Gotsman, C., and Attene, M. 2005. Recent advances in remeshing of surfaces. ftp://ftp-sop.inria.fr/geometrica/alliez/survey_remeshing.pdf.]]Google Scholar
3. Banchoff, T. F. 1967. Critical points and curvature for embedded polyhedral surfaces. Differential Geometry, 3, 1, 257–268.]]Google Scholar
4. Bern, M. W., and Eppstein, D. 1995. Mesh generation and optimal triangulation. In Computing in Euclidean Geometry, Lecture Notes on Computing #4. World Scientific, 47–123.]]Google Scholar
5. Boier-Martin, I., Rushmeier, H., and Jin, J. 2004. Parameterization of triangle meshes over quadrilateral domains. In Proc. Eurographics Symposium on Geometry Processing, 197–207.]] Google ScholarDigital Library
6. Bremer, P.-T., Edelsbrunner, H., Hamann, B., and Pascucci, V. 2004. A topological hierarchy for functions on triangulated surfaces. TVCG 10, 4, 385–396.]]Google ScholarDigital Library
7. Chung, F. R. K. 1997. Spectral Graph Theory. American Mathematical Society.]]Google Scholar
8. Courant, R., and Hilbert, D. 1953. Methods of Mathematical Physics, vol. I. Interscience Publishers, New York.]]Google Scholar
9. Dong, S., Kircher, S., and Garland, M. 2005. Harmonic functions for quadrilateral remeshing of arbitrary manifolds. CAGD 22, 5, 392–423.]]Google ScholarCross Ref
10. Eck, M., and Hoppe, H. 1996. Automatic reconstruction of B-spline surfaces of arbitrary topological type. In Proc. SIGGRAPH, 325–334.]] Google ScholarDigital Library
11. Eck, M., DeRose, T. D., Duchamp, T., Hoppe, H., Louns-Bery, M., and Stuetzle, W. 1995. Multiresolution analysis of arbitrary meshes. In Proc. SIGGRAPH, 173–182.]] Google ScholarDigital Library
12. Edelsbrunner, H., Letscher, D., and Zomorodian, A. 2002. Topological persistence and simplification. Discrete Comput. Geom. 28, 511–533.]]Google ScholarDigital Library
13. Edelsbrunner, H., Harer, J., and Zomorodian, A. 2003. Hierarchical Morse-Smale complexes for piecewise linear 2-manifolds. Discrete Comput. Geom. 30, 87–107.]]Google ScholarCross Ref
14. Floater, M. S., and Hormann, K. 2004. Surface parameterization: A tutorial and survey. In Multiresolution in Geometric Modelling.]]Google Scholar
15. Floater, M. S. 2003. Mean value coordinates. Computer Aided Geometric Design 20, 1 (Mar.), 19–27.]] Google ScholarDigital Library
16. Friedel, I., Schröder, P., and Khodakovsky, A. 2004. Variational normal meshes. TOG 23, 4, 1061–1073.]] Google ScholarDigital Library
17. Garland, M., and Heckbert, P. S. 1997. Surface simplification using quadric error metrics. In Proc. SIGGRAPH, 209–216.]] Google ScholarDigital Library
18. Garland, M. 1999. Multiresolution modeling: Survey & future opportunities. In State of the Art Report, Eurographics, 111–131.]]Google Scholar
19. Gu, X., Gortler, S. J., and Hoppe, H. 2002. Geometry images. TOG 21, 3, 355–361. (Proc. SIGGRAPH).]] Google ScholarDigital Library
20. Guskov, I., Vidimce, K., Sweldens, W., and Schröder, P. 2000. Normal meshes. In Proc. SIGGRAPH, 95–102.]] Google ScholarDigital Library
21. Halstead, M., Kass, M., and DeRose, T. 1993. Efficient, fair interpolation using Catmull-Clark surfaces. In Proc. SIGGRAPH, 35–44.]] Google ScholarDigital Library
22. Hilaga, M., Shinagawa, Y., Kohmura, T., and Kunii, T. L. 2001. Topology matching for fully automatic similarity estimation of 3D shapes. In Proc. SIGGRAPH, 203–212.]] Google ScholarDigital Library
23. Hormann, K., and Greiner, G. 2000. Quadrilateral remeshing. In Proc. Vision Modeling and Visualization, 153–162.]]Google Scholar
24. Karni, Z., and Gotsman, C. 2000. Spectral compression of mesh geometry. In Proc. SIGGRAPH, 279–286.]] Google ScholarDigital Library
25. Khodakovsky, A., Litke, N., and Schröder, P. 2003. Globally smooth parameterizations with low distortion. TOG 22, 3, 350–357. (Proc. SIGGRAPH).]] Google ScholarDigital Library
26. Koren, Y., Carmel, L., and Harel, D. 2002. ACE:A fast multiscale eigenvector computation for drawing huge graphs. In Proc. InfoVis ’02, 137–144.]] Google ScholarDigital Library
27. Lee, A. W. F., Sweldens, W., Schröder, P., Cowsar, L., and Dobkin, D. 1998. MAPS: Multiresolution adaptive parameterization of surfaces. In Proc. SIGGRAPH, 95–104.]] Google ScholarDigital Library
28. Marinov, M., and Kobbelt, L. 2004. Direct anisotropic quad-dominant remeshing. In Proc. Pacific Graphics.]] Google ScholarDigital Library
29. Ni, X., Garland, M., and Hart, J. C. 2004. Fair Morse functions for extracting the topological structure of a surface mesh. TOG 23, 3, 613–622. (Proc. SIGGRAPH).]] Google ScholarDigital Library
30. Owen, S., Staten, M. L., Canann, S. A., and Saigal, S. 1999. Q-Morph: An indirect approach to advancing front quad meshing. Intl. J. Num. Methods in Engineering 9, 1317–1340.]]Google ScholarCross Ref
31. Pascucci, V., and Cole-McLaughlin, K. 2002. Efficient computation of the topology of level sets. In Proc. Visualization, 187–194.]] Google ScholarDigital Library
32. Pinkall, U., and Polthier, K. 1993. Computing discrete minimal surfaces and their conjugates. Exp. Math. 2, 1, 15–36.]]Google ScholarCross Ref
33. Ray, N., Li, W. C., Levy, B., Sheffer, A., and Alliez, P. 2005. Periodic global parameterization. TOG. (Accepted, pending revision).]] Google ScholarDigital Library
34. Sander, P. V., Wood, Z. J., Gortler, S. J., Snyder, J., and Hoppe, H. 2003. Multi-chart geometry images. In Proc. Eurographics Symposium on Geometry Processing, 146–155.]] Google ScholarDigital Library
35. Schreiner, J., Asirvatham, A., Praun, E., and Hoppe, H. 2004. Inter-surface mapping. TOG 23, 3, 870–877. (Proc. SIGGRAPH).]] Google ScholarDigital Library
36. Shimada, K., Liao, J.-H., and Itoh, T. 1998. Quadrilateral meshing with directionality control through the packing of square cells. In Seventh Int’l Meshing Roundtable, 61–75.]]Google Scholar
37. Stam, J. 2003. Flows on surfaces of arbitrary topology. TOG 22, 3, 724–731. (Proc. SIGGRAPH).]] Google ScholarDigital Library
38. Stander, B. T., and Hart, J. C. 1997. Guaranteeing the topology of implicit surface polygonization for interactive modeling. In Proc. SIGGRAPH, 279–286.]] Google ScholarDigital Library
39. Taubin, G. 2000. Geometric signal processing on polygonal meshes. In State of the Art Report, Eurographics, 81–96.]]Google Scholar
40. van Kreveld, M. J., van Oostrum, R., Bajaj, C. L., Pas-Cucci, V., and Schikore, D. 1997. Contour trees and small seed sets for isosurface traversal. In Sym. Comp. Geo., 212–220.]] Google ScholarDigital Library
41. Velho, L., and Zorin, D. 2001. 4-8 subdivision. CAGD 18, 5, 397–427. Spec. Issue on Subdiv. Techniques.]]Google ScholarDigital Library
42. Weber, G., Scheuermann, G., Hagen, H., and Hamann, B. 2002. Exploring scalar fields using critical isovalues. In Proc. Visualization, 171–178.]] Google ScholarDigital Library
43. Ying, L., and Zorin, D. 2004. A simple manifold-based construction of surfaces of arbitrary smoothness. TOG 23, 3, 271–275. (Proc. SIGGRAPH).]] Google ScholarDigital Library