“Subdivision exterior calculus for geometry processing”
Conference:
Type(s):
Title:
- Subdivision exterior calculus for geometry processing
Session/Category Title:
- MESHES & FIELDS
Presenter(s)/Author(s):
Moderator(s):
Abstract:
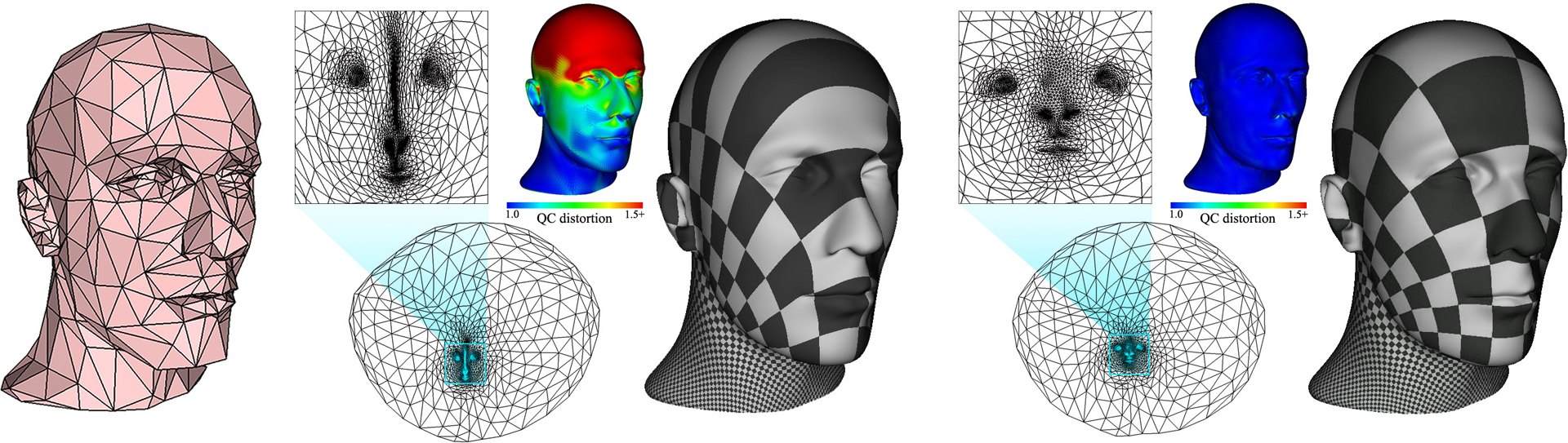
This paper introduces a new computational method to solve differential equations on subdivision surfaces. Our approach adapts the numerical framework of Discrete Exterior Calculus (DEC) from the polygonal to the subdivision setting by exploiting the refin-ability of subdivision basis functions. The resulting Subdivision Exterior Calculus (SEC) provides significant improvements in accuracy compared to existing polygonal techniques, while offering exact finite-dimensional analogs of continuum structural identities such as Stokes’ theorem and Helmholtz-Hodge decomposition. We demonstrate the versatility and efficiency of SEC on common geometry processing tasks including parameterization, geodesic distance computation, and vector field design.
References:
1. Alexa, M., and Wardetzky, M. 2011. Discrete Laplacians on general polygonal meshes. ACM Trans. Graph. 30, 4, Art. 102. Google ScholarDigital Library
2. Arnold, D. N., Falk, R. S., and Winther, R. 2006. Finite element exterior calculus, homological techniques, and applications. Acta Numerica 15, 1–155.Google ScholarCross Ref
3. Auchmann, B., and Kurz, S. 2006. A geometrically defined discrete Hodge operator on simplicial cells. IEEE Trans. on Magnetics 42, 4, 643–646.Google ScholarCross Ref
4. Babuska, I., and Suri, M. 1994. The p and h-p versions of the finite element method: Basic principles and properties. SIAM Review 36, 4, 578–632. Google ScholarDigital Library
5. Back, A., and Sonnendrücker, E. 2014. Finite element Hodge for spline discrete differential forms: Application to the Vlasov-Poisson system. Appl. Numer. Math. 79, 124–136. Google ScholarDigital Library
6. Barendrecht, P. J. 2013. Isogeometric Analysis for Subdivision Surfaces. Master’s thesis, Eindhoven University of Technology.Google Scholar
7. Bossavit, A., Ed. 1998. Computational Electromagnetism. Academic Press.Google Scholar
8. Bossavit, A. 2000. Computational electromagnetism and geometry. (5): The ‘Galerkin Hodge’. J. Japan Soc. Appl. Electromagn. & Mech. 8, 2, 203–9.Google Scholar
9. Botsch, M., Kobbelt, L., Pauly, M., Alliez, P., and Lévy, B. 2010. Polygon Mesh Processing. AK Peters.Google Scholar
10. Buffa, A., Rivas, J., Sangalli, G., and Vázquez, R. 2011. Isogeometric discrete differential forms in three dimensions. SIAM J. Numer. Anal. 49, 2, 818–844. Google ScholarDigital Library
11. Buffa, A., Sangalli, G., and Vázquez, R. 2014. Isogeometric methods for computational electromagnetics: B-spline and T-spline discretizations. J. Comput. Phys. 257, 1291–1320. Google ScholarDigital Library
12. Cirak, F., Scott, M. J., Antonsson, E. K., Ortiz, M., and Schröder, P. 2002. Integrated modeling, finite-element analysis, and engineering design for thin-shell structures using subdivision. Comput. Aided Des. 34, 137–148.Google ScholarCross Ref
13. Cottrell, J. A., Hughes, T. J. R., and Bazilevs, Y. 2009. Isogeometric Analysis: Toward Integration of CAD and FEA. Wiley Publishing. Google ScholarCross Ref
14. Crane, K., de Goes, F., Desbrun, M., and Schröder, P. 2013. Digital geometry processing with discrete exterior calculus. In ACM SIGGRAPH Courses. Google ScholarDigital Library
15. Crane, K., Weischedel, C., and Wardetzky, M. 2013. Geodesics in heat: A new approach to computing distance based on heat flow. ACM Trans. Graph. 32, 5, Art. 152. Google ScholarDigital Library
16. Dahmen, W. 1986. Subdivision algorithms converge quadratically. J. Comput. Appl. Math. 16, 2, 145–158. Google ScholarDigital Library
17. de Goes, F., Memari, P., Mullen, P., and Desbrun, M. 2014. Weighted triangulations for geometry processing. ACM Trans. Graph. 33, 3, Art. 28. Google ScholarDigital Library
18. Desbrun, M., Meyer, M., Schröder, P., and Barr, A. H. 1999. Implicit fairing of irregular meshes using diffusion and curvature flow. ACM SIGGRAPH, 317–324. Google ScholarDigital Library
19. Desbrun, M., Kanso, E., and Tong, Y. 2008. Discrete differential forms for computational modeling. In Discrete Differential Geometry, A. I. Bobenko et al. (Eds), vol. 38 of Oberwolfach Seminars. 287–324.Google Scholar
20. Elcott, S., Tong, Y., Kanso, E., Schröder, P., and Desbrun, M. 2007. Stable, circulation-preserving, simplicial fluids. ACM Trans. Graph. 26, 1, Art. 4. Google ScholarDigital Library
21. Fisher, M., Schröder, P., Desbrun, M., and Hoppe, H. 2007. Design of tangent vector fields. ACM Trans. Graph. 26, 3, Art. 56. Google ScholarDigital Library
22. Frankel, T. 2004. The Geometry of Physics: An Introduction. Cambridge University Press.Google Scholar
23. Grinspun, E., Krysl, P., and Schröder, P. 2002. CHARMS: A simple framework for adaptive simulation. ACM Trans. Graph. 21, 3, 281–290. Google ScholarDigital Library
24. He, L., Schaefer, S., and Hormann, K. 2010. Parameterizing subdivision surfaces. ACM Trans. Graph. 29, 4, Art. 120. Google ScholarDigital Library
25. Hirani, A. 2003. Discrete Exterior Calculus. PhD thesis, Caltech. Google ScholarDigital Library
26. Hughes, T., Cottrell, J., and Bazilevs, Y. 2005. Isogeometric analysis: CAD, finite elements, NURBS, exact geometry and mesh refinement. Comput. Methods Appl. Mech. Eng. 194, 39-41, 4135–4195.Google ScholarCross Ref
27. Jüttler, B., Mantzaflaris, A., Perl, R., and Rumpf, M. 2016. On numerical integration in isogeometric subdivision methods for PDEs on surfaces. Comput. Methods Appl. Mech. Eng. 302, 131–146.Google ScholarCross Ref
28. Liu, S., Jacobson, A., and Gingold, Y. 2014. Skinning cubic Bézier splines and Catmull-Clark subdivision surfaces. ACM Trans. Graph. 33, 6, Art. 190. Google ScholarDigital Library
29. Liu, B., Mason, G., Hodgson, J., Tong, Y., and Desbrun, M. 2015. Model-reduced variational fluid simulation. ACM Trans. Graph. 34, 6, Art. 244. Google ScholarDigital Library
30. Loop, C., van Gelder, D., Litke, N., El Guerrab, R., Elmieh, B., and Kraemer, M. 2013. OpenSubdiv from research to industry adoption. In ACM SIGGRAPH Courses. Google ScholarDigital Library
31. Lounsbery, M., DeRose, T. D., and Warren, J. 1997. Multiresolution analysis for surfaces of arbitrary topological type. ACM Trans. Graph. 16, 1, 34–73. Google ScholarDigital Library
32. McCormick, S. F. 1984. Multigrid Methods for Variational Problems: Further Results. SIAM J. Numer. Anal. 21, 2, 255–263.Google ScholarCross Ref
33. Mullen, P., Tong, Y., Alliez, P., and Desbrun, M. 2008. Spectral conformal parameterization. Comput. Graph. Forum 27, 5, 1487–1494. Google ScholarDigital Library
34. Mullen, P., Memari, P., de Goes, F., and Desbrun, M. 2011. HOT: Hodge-optimized triangulations. ACM Trans. Graph. 30, 4, Art. 103. Google ScholarDigital Library
35. Munkres, J. R. 1984. Elements of Algebraic Topology. Addison-Wesley.Google Scholar
36. Nguyen, T., Karčiauskas, K., and Peters, J. 2014. A comparative study of several classical, discrete differential and isogeometric methods for solving Poissons equation on the disk. Axioms, 3, 280–299.Google ScholarCross Ref
37. Niessner, M., Loop, C., Meyer, M., and Derose, T. 2012. Feature-adaptive GPU rendering of Catmull-Clark subdivision surfaces. ACM Trans. Graph. 31, 1, Art. 6. Google ScholarDigital Library
38. Riffnaller-Schiefer, A., Augsdörfer, U. H., and Fellner, D. W. 2015. Isogeometric Analysis for Modelling and Design. In Eurographics (short papers).Google Scholar
39. Stam, J. 1998. Exact evaluation of Catmull-Clark subdivision surfaces at arbitrary parameter values. ACM SIGGRAPH, 395–404. Google ScholarDigital Library
40. Stam, J. 2003. Flows on surfaces of arbitrary topology. ACM Trans. Graph. 22, 3, 724–731. Google ScholarDigital Library
41. Strang, G., and Fix, G. 1973. An Analysis of the Finite Element Method. Wellesley-Cambridge.Google Scholar
42. Thomaszewski, B., Wacker, M., and Strasser, W. 2006. A consistent bending model for cloth simulation with corota-tional subdivision finite elements. In Symp. Comp. Anim., 107–116. Google ScholarDigital Library
43. Wang, K., Weiwei, Tong, Y., Desbrun, M., and Schröder, P. 2006. Edge subdivision schemes and the construction of smooth vector fields. ACM Trans. Graph. 25, 3, 1041–1048. Google ScholarDigital Library
44. Wang, K. 2008. A subdivision approach to the construction of smooth differential forms. PhD thesis, Caltech. Google ScholarDigital Library
45. Wardetzky, M., Mathur, S., Kälberer, F., and Grinspun, E. 2007. Discrete Laplace operators: No free lunch. In Symp. Geom. Process., 33–37. Google ScholarDigital Library
46. Warren, J., and Weimer, H. 2001. Subdivision Methods for Geometric Design: A Constructive Approach. Morgan Kaufmann Publishers Inc. Google ScholarDigital Library
47. Whitney, H. 1957. Geometric Integration Theory. Princeton University Press.Google Scholar
48. Zhou, K., Huang, X., Xu, W., Guo, B., and Shum, H.-Y. 2007. Direct manipulation of subdivision surfaces on GPUs. ACM Trans. Graph. 26, 3, Art. 91. Google ScholarDigital Library
49. Zorin, D., and Schröder, P. 2000. Subdivision for modeling and animation. In ACM SIGGRAPH Courses.Google Scholar