“Subdivision Directional Fields” by Custers and Vaxman
Conference:
Type(s):
Title:
- Subdivision Directional Fields
Session/Category Title: Geometric Foundations
Presenter(s)/Author(s):
Abstract:
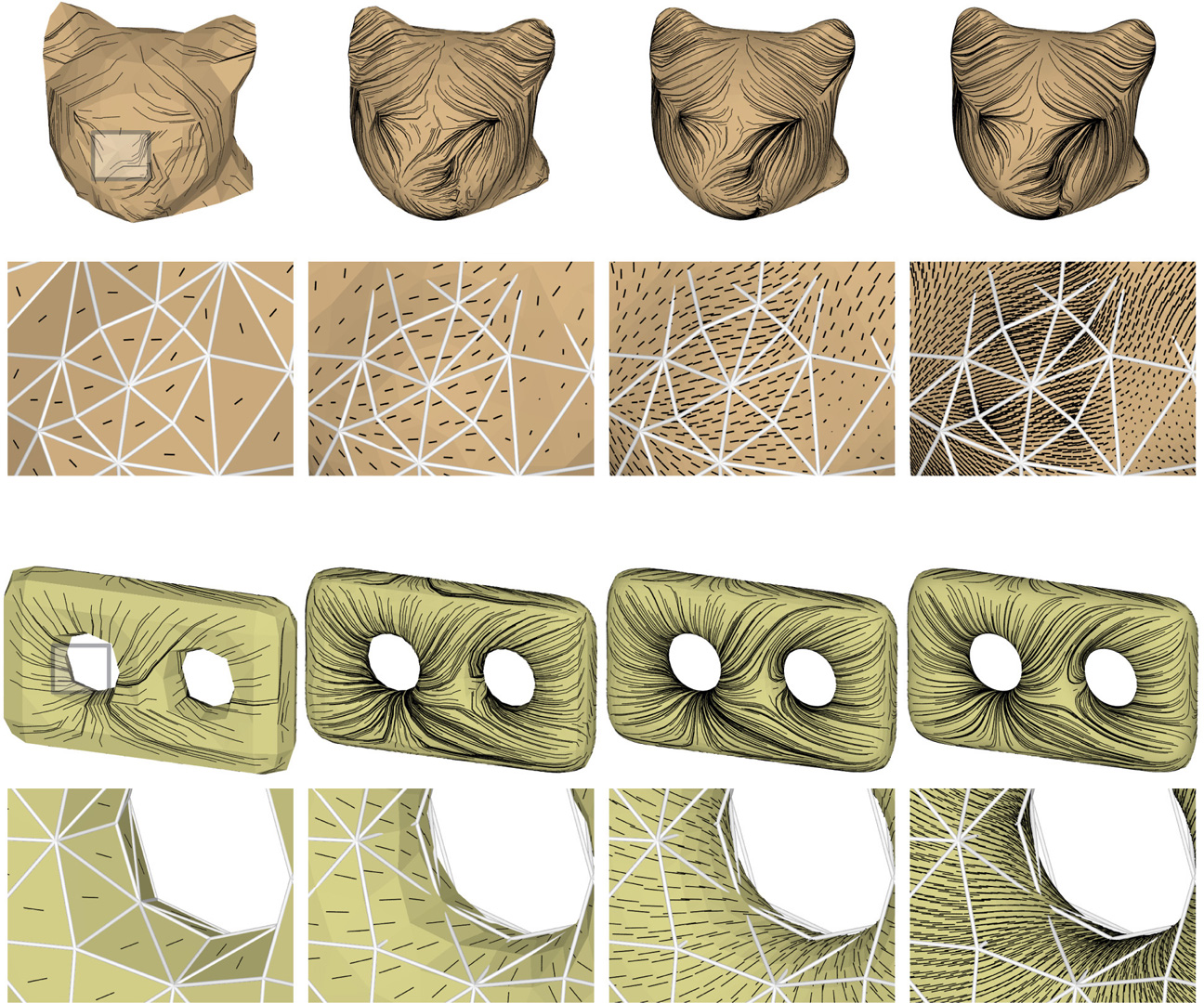
We present a novel linear subdivision scheme for face-based tangent directional fields on triangle meshes. Our subdivision scheme is based on a novel coordinate-free representation of directional fields as halfedge-based scalar quantities, bridging the mixed finite-element representation with discrete exterior calculus. By commuting with differential operators, our subdivision is structure preserving: it reproduces curl-free fields precisely and reproduces divergence-free fields in the weak sense. Moreover, our subdivision scheme directly extends to directional fields with several vectors per face by working on the branched covering space. Finally, we demonstrate how our scheme can be applied to directional-field design, advection, and robust earth mover’s distance computation, for efficient and robust computation.