“Spacetime constraints” by Witkin and Kass

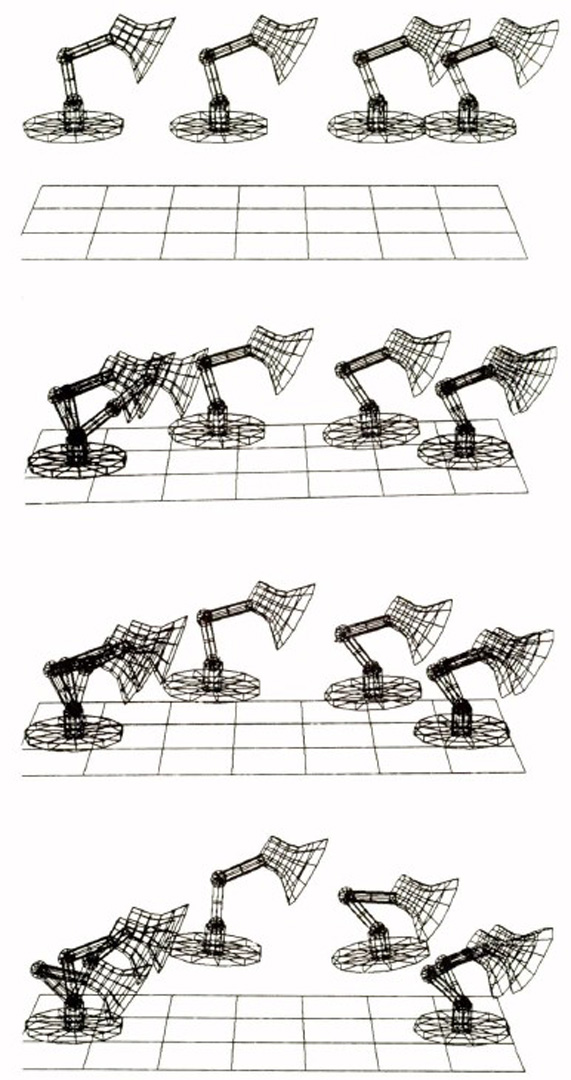
Spacetime constraints are a new method for creating character animation. The animator specifies what the character has to do, for instance, “jump from here to there, clearing a hurdle in between;” how the motion should be performed, for instance “don’t waste energy,” or “come down hard enough to splatter whatever you land on;” the character’s physical structure—the geometry, mass, connectivity, etc. of the parts; and the physical resources’ available to the character to accomplish the motion, for instance the character’s muscles, a floor to push off from, etc. The requirements contained in this description, together with Newton’s laws, comprise a problem of constrained optimization. The solution to this problem is a physically valid motion satisfying the “what” constraints and optimizing the “how” criteria. We present as examples a Luxo lamp performing a variety of coordinated motions. These realistic motions conform to such principles of traditional animation as anticipation, squash-and-stretch, follow-through, and timing.

1. William W. Armstrong and Mark W. Green, The dynamics of articulated rigid bodies for purposes of animation, in Visual Computer, Springer-Verlag, 1985, pp. 231-240.
2. Ronen Barzel and Alan H. Barr, Dynamic Consiraints, Topics in Physically Based Modeling, Course Notes, Vol. 16, Siggraph 1987
3. Michael Brady et. el., eds, Robot Motion: Planning and Control, MIT Press, Cambridge, MA, 1982
4. Charles E. Buckley, The Application of Continuum Methods to Path Planning, Doctoral Dissertation, Dept. of Mechanical Engineering, Stanford University, Stanford, CA, 1985
5. Kurt Fleischer and Andrew Witkin, A modeling testbed, Proc. Graphics Interface, 1988.
6. Phillip Gill, Welter Murray, and Margret Wright, Practical Optimization, Academic Press, New York, NY, 1981
7. Michael Girard and Anthony a Maciejewski, Computataional Modeling/or the Computer Animation of Legged Figures, Proc. SIGGRAPH, 1985, pp. 263- 270
8. Herbert Goldstein, Classical Mechanics, Addison Wesley, Reading, MA, 1950
9. David Haumarm, Modeling the Physical Behavior of Flezible Objects, Topics in Physically Based Modeling, Course Notes, Vol. 16, Siggraph 1987
10. Paul Isaacs and Michael Cohen, Controlling Dynamic Simulation with Kinematic Constraints, Behavior Functions and Inverse Dynamics, Proc. Siggraph 1987, pp. 215-224
11. Charles Klein and Ching-Hsiang Huang, Review of Pseudoinverse Control for Use with Kinematically Redundant Manipulators, IEEE Trans. SMC, Vol. 13, No. 3, 1983
12. John Lasseter, Principles of Traditional Animation Applied to 3D Computer Animation, Proc. Siggraph 1987, pp. 35-44
13. Pixar, Luzo, Jr., (film,) 1986
14. William Press et. al., Numerical Recipes, Cambridge University Press, Cambridge, Engiemd, 1986
15. Robert S. Stengel, Stochastic Optimal Control, John Wiley and Sons, New York, 1986.
16. Demetri Terzopoulos, John Platt, Alan Barr, and Kart Fleischer, Elastically Deformable Models, Pros. SIGGRAPH, 1987.
17. Jane Wilhelms and Brian Barsky, Using Dynamic Analysis To Animate Articulated Bodies Such As Humans and Robots, Graphics Interface, 1985.
18. Andrew Witkin, Kurt Fleischer, and Alan Barr, Energy constraints on parameterized models, Computer Graphics, 21 (4) July 1987, pp. 225-232 (Proc. SIG- GRAPH ’87).