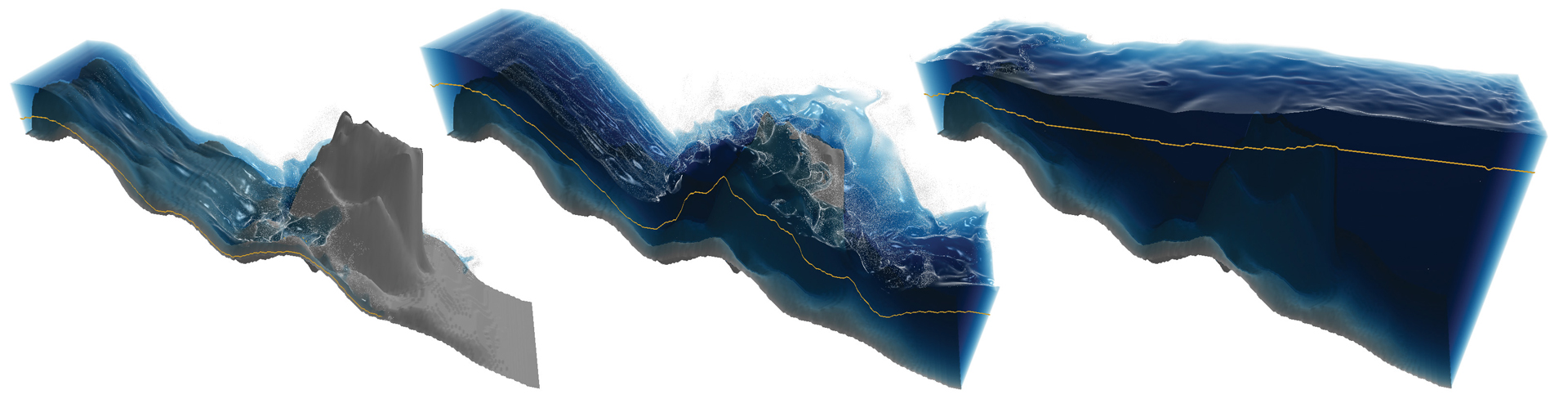
“Real-time Eulerian water simulation using a restricted tall cell grid” by Chentanez and Müller-Fischer

We present a new Eulerian fluid simulation method, which allows real-time simulations of large scale three dimensional liquids. Such scenarios have hitherto been restricted to the domain of off-line computation. To reduce computation time we use a hybrid grid representation composed of regular cubic cells on top of a layer of tall cells. With this layout water above an arbitrary terrain can be represented without consuming an excessive amount of memory and compute power, while focusing effort on the area near the surface where it most matters. Additionally, we optimized the grid representation for a GPU implementation of the fluid solver. To further accelerate the simulation, we introduce a specialized multi-grid algorithm for solving the Poisson equation and propose solver modifications to keep the simulation stable for large time steps. We demonstrate the efficiency of our approach in several real-world scenarios, all running above 30 frames per second on a modern GPU. Some scenes include additional features such as two-way rigid body coupling as well as particle representations of sub-grid detail.

1. Adalsteinsson, D., and Sethian, J. A. 1997. The fast construction of extension velocities in level set methods. Journal of Computational Physics 148, 2–22. Google ScholarDigital Library
2. Adams, B., Pauly, M., Keiser, R., and Guibas, L. J. 2007. Adaptively sampled particle fluids. In Proc. SIGGRAPH, 48. Google Scholar
3. Bargteil, A. W., Goktekin, T. G., O’Brien, J. F., and Strain, J. A. 2005. A semi-lagrangian contouring method for fluid simulation. ACM Transactions on Graphics. Google Scholar
4. Batty, C., Bertails, F., and Bridson, R. 2007. A fast variational framework for accurate solid-fluid coupling. In Proc. SIGGRAPH, 100. Google Scholar
5. Batty, C., Xenos, S., and Houston, B. 2010. Tetrahedral embedded boundary methods for accurate and flexible adaptive fluids. In Proc. Eurographics.Google Scholar
6. Bridson, R. 2008. Fluid Simulation for Computer Graphics. A K Peters. Google Scholar
7. Brochu, T., and Bridson, R. 2009. Robust topological operations for dynamic explicit surfaces. SIAM Journal on Scientific Computing 31, 4, 2472–2493. Google ScholarDigital Library
8. Brochu, T., Batty, C., and Bridson, R. 2010. Matching fluid simulation elements to surface geometry and topology. In Proc. SIGGRAPH, 1–9. Google Scholar
9. Carlson, M., Mucha, P. J., and Turk, G. 2004. Rigid fluid: animating the interplay between rigid bodies and fluid. In Proc. SIGGRAPH, 377–384. Google Scholar
10. Chentanez, N., and Müller-Fischer, M. 2010. Real-time simulation of large bodies of water with small scale details. In Proc. ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Google ScholarDigital Library
11. Chentanez, N., Goktekin, T. G., Feldman, B. E., and O’Brien, J. F. 2006. Simultaneous coupling of fluids and deformable bodies. In Proc. ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 83–89. Google Scholar
12. Chentanez, N., Feldman, B. E., Labelle, F., O’Brien, J. F., and Shewchuk, J. R. 2007. Liquid simulation on lattice-based tetrahedral meshes. In Proc. ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 219–228. Google ScholarDigital Library
13. Cohen, J. M., Tariq, S., and Green, S. 2010. Interactive fluid-particle simulation using translating eulerian grids. In Proc. ACM SIGGRAPH symposium on Interactive 3D Graphics and Games, 15–22. Google Scholar
14. Crane, K., Llamas, I., and Tariq, S. 2007. Real-time simulation and rendering of 3d fluids. In GPU Gems 3, H. Nguyen, Ed. Addison Wesley Professional, August, ch. 30.Google Scholar
15. Enright, D., and Fedkiw, R. 2002. Robust treatment of interfaces for fluid flows and computer graphics. In Computer Graphics, 9th Int. Conf. on Hyperbolic Problems Theory, Numerics, Applications.Google Scholar
16. Enright, D., Marschner, S., and Fedkiw, R. 2002. Animation and rendering of complex water surfaces. In Proc. SIGGRAPH, 736–744. Google Scholar
17. Enright, D., Nguyen, D., Gibou, F., and Fedkiw, R. 2003. Using the particle level set method and a second order accurate pressure boundary condition for free surface flows. In In Proc. 4th ASME-JSME Joint Fluids Eng. Conf., number FEDSM200345144. ASME, 2003–45144.Google Scholar
18. Feldman, B. E., O’Brien, J. F., and Klingner, B. M. 2005. Animating gases with hybrid meshes. In Proc. SIGGRAPH, 904–909. Google Scholar
19. Foster, N., and Fedkiw, R. 2001. Practical animation of liquids. In Proc. SIGGRAPH, 23–30. Google Scholar
20. Foster, N., and Metaxas, D. 1996. Realistic animation of liquids. Graph. Models Image Process. 58, 5, 471–483. Google ScholarDigital Library
21. Guendelman, E., Selle, A., Losasso, F., and Fedkiw, R. 2005. Coupling water and smoke to thin deformable and rigid shells. In Proc. SIGGRAPH, 973–981. Google Scholar
22. Holmberg, N., and Wünsche, B. C. 2004. Efficient modeling and rendering of turbulent water over natural terrain. In Proc. GRAPHITE, 15–22. Google Scholar
23. Irving, G., Guendelman, E., Losasso, F., and Fedkiw, R. 2006. Efficient simulation of large bodies of water by coupling two- and three-dimensional techniques. In Proc. SIGGRAPH, 805–811. Google Scholar
24. Jeong, W.-K., Ross, and Whitaker, T. 2007. A fast eikonal equation solver for parallel systems. In SIAM conference on Computational Science and Engineering.Google Scholar
25. Kim, D., Song, O.-Y., and Ko, H.-S. 2008. A semi-lagrangian cip fluid solver without dimensional splitting. Computer Graphics Forum 27, 2 (April), 467–475.Google ScholarCross Ref
26. Klingner, B. M., Feldman, B. E., Chentanez, N., and O’Brien, J. F. 2006. Fluid animation with dynamic meshes. In Proc. SIGGRAPH, 820–825. Google Scholar
27. Lentine, M., Zheng, W., and Fedkiw, R. 2010. A novel algorithm for incompressible flow using only a coarse grid projection. In Proc. SIGGRAPH, 114:1–114:9. Google Scholar
28. Long, B., and Reinhard, E. 2009. Real-time fluid simulation using discrete sine/cosine transforms. In Proc. ACM SIGGRAPH symposium on Interactive 3D Graphics and Games, 99–106. Google Scholar
29. Losasso, F., Gibou, F., and Fedkiw, R. 2004. Simulating water and smoke with an octree data structure. In Proc. SIGGRAPH, 457–462. Google Scholar
30. Losasso, F., Talton, J., Kwatra, N., and Fedkiw, R. 2008. Two-way coupled sph and particle level set fluid simulation. IEEE Transactions on Visualization and Computer Graphics 14, 4, 797–804. Google ScholarDigital Library
31. McAdams, A., Sifakis, E., and Teran, J. 2010. A parallel multigrid poisson solver for fluids simulation on large grids. In Proc. ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Google ScholarDigital Library
32. Molemaker, J., Cohen, J. M., Patel, S., and Noh, J. 2008. Low viscosity flow simulations for animation. In ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 9–18. Google ScholarDigital Library
33. Müller, M., Charypar, D., and Gross, M. 2003. Particle-based fluid simulation for interactive applications. In ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 154–159. Google ScholarDigital Library
34. Müller, M. 2009. Fast and robust tracking of fluid surfaces. In Proc. ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Google Scholar
35. Neyret, F. 2003. Advected textures. In Proc. ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 147–153. Google Scholar
36. Premoze, S., Tasdizen, T., Bigler, J., Lefohn, A. E., and Whitaker, R. T. 2003. Particle-based simulation of fluids. Comput. Graph. Forum 22, 3, 401–410.Google ScholarCross Ref
37. Rasmussen, N., Enright, D., Nguyen, D., Marino, S., Sumner, N., Geiger, W., Hoon, S., and Fedkiw, R. 2004. Directable photorealistic liquids. In Proc. ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 193–202. Google Scholar
38. Robinson-Mosher, A., Shinar, T., Gretarsson, J., Su, J., and Fedkiw, R. 2008. Two-way coupling of fluids to rigid and deformable solids and shells. ACM Trans. Graph. 27 (August), 46:1–46:9. Google ScholarDigital Library
39. Sanders, J., and Kandrot, E. 2010. CUDA by Example: An Introduction to General-Purpose GPU Programming. Addison-Wesley Professional. Google ScholarDigital Library
40. Selle, A., Fedkiw, R., Kim, B., Liu, Y., and Rossignac, J. 2008. An unconditionally stable MacCormack method. J. Sci. Comput. 35, 2-3, 350–371. Google ScholarDigital Library
41. Sin, F., Bargteil, A. W., and Hodgins, J. K. 2009. A point-based method for animating incompressible flow. In Proc. ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 247–255. Google Scholar
42. Solenthaler, B., and Pajarola, R. 2009. Predictive-corrective incompressible sph. In Proc. SIGGRAPH, 1–6. Google Scholar
43. Stam, J. 1999. Stable fluids. In Proc. SIGGRAPH, 121–128. Google Scholar
44. Takahashi, T., Ueki, H., Kunimatsu, A., and Fujii, H. 2002. The simulation of fluid-rigid body interaction. In ACM SIGGRAPH conference abstracts and applications, 266–266. Google Scholar
45. Thürey, N., and Rüde, U. 2004. Free Surface Lattice-Boltzmann fluid simulations with and without level sets. Proc. of Vision, Modelling, and Visualization VMV, 199–207.Google Scholar
46. Thürey, N., and Rüde, U. 2009. Stable free surface flows with the lattice Boltzmann method on adaptively coarsened grids. Computing and Visualization in Science 12 (5). Google ScholarCross Ref
47. Thurey, N., Muller-Fischer, M., Schirm, S., and Gross, M. 2007. Real-time breakingwaves for shallow water simulations. In Proc. Pacific Conf. on CG and App., 39–46. Google Scholar
48. Štava, O., Beneš, B., Brisbin, M., and Křivánek, J. 2008. Interactive terrain modeling using hydraulic erosion. In Proc. ACM SIGGRAPH/Eurographics Symposium on Computer Animation, 201–210. Google ScholarDigital Library
49. Wojtan, C., Thürey, N., Gross, M., and Turk, G. 2010. Physics-inspired topology changes for thin fluid features. In Proc. SIGGRAPH, no. 4, 1–8. Google Scholar
50. Yu, J., and Turk, G. 2010. Enhancing fluid animation with adaptive, controllable and intermittent turbulence. In Proc. ACM SIGGRAPH/Eurographics Symposium on Computer Animation. Google ScholarDigital Library
51. Zhu, Y., and Bridson, R. 2005. Animating sand as a fluid. In Proc. SIGGRAPH, 965–972. Google Scholar