“Progressive geometry compression” by Khodakovsky, Schröder and Sweldens

  • ©

Conference:


Type(s):


Title:

    Progressive geometry compression

Presenter(s)/Author(s):


Abstract:


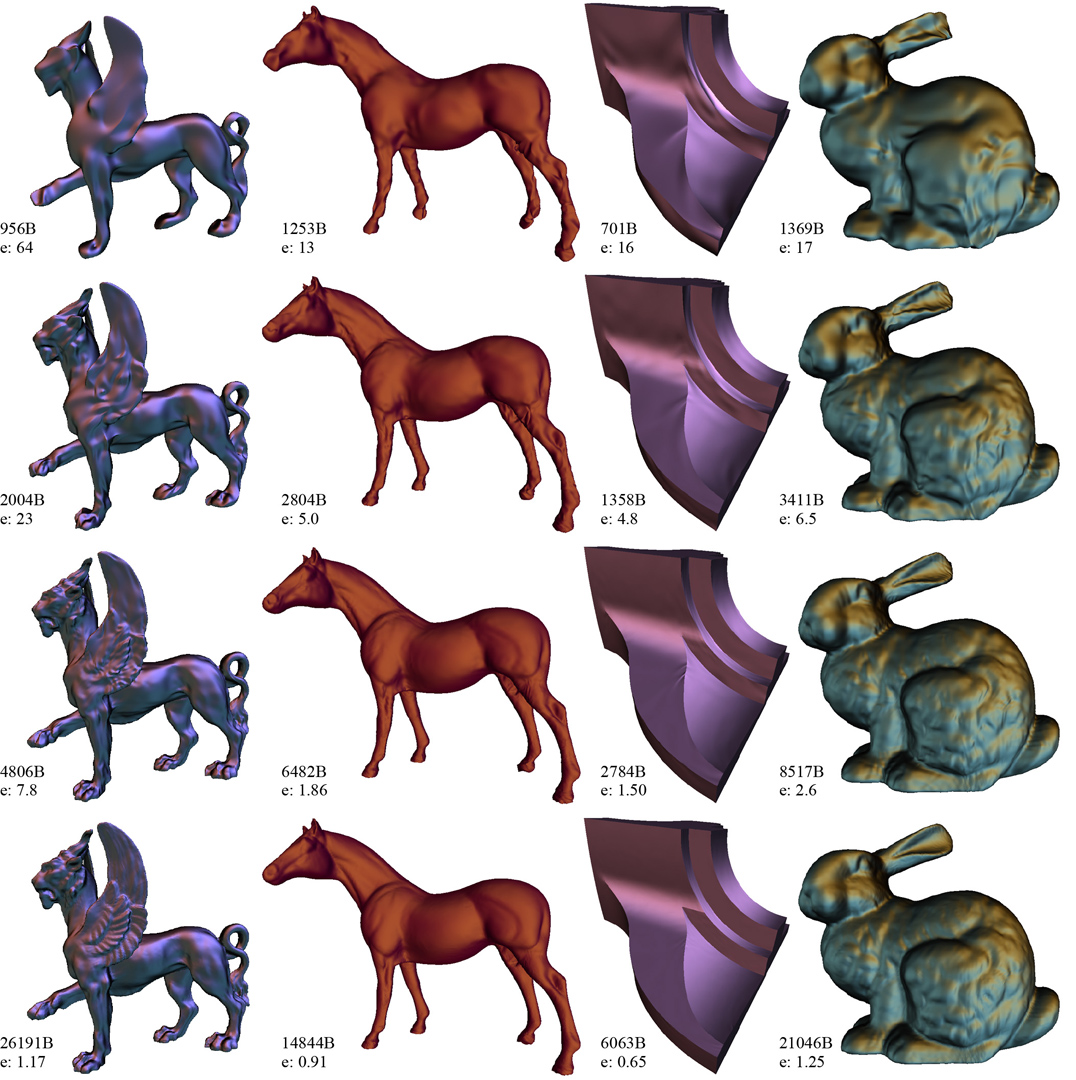
    We propose a new progressive compression scheme for arbitrary topology, highly detailed and densely sampled meshes arising from geometry scanning. We observe that meshes consist of three distinct components: geometry, parameter, and connectivity information. The latter two do not contribute to the reduction of error in a compression setting. Using semi-regular meshes, parameter and connectivity information can be virtually eliminated. Coupled with semi-regular wavelet transforms, zerotree coding, and subdivision based reconstruction we see improvements in error by a factor four (12dB) compared to other progressive coding schemes.

References:


    1. BAJAJ, C. L., PASCUCCI, V., AND ZHUANG, G. Progressive Compression and Transmission of Arbitrary Triangular Meshes. IEEE Visualization ’99 (1999), 307-316. 
    2. CERTAIN, A., POPOVIC, J., DEROSE, T., DUCHAMP, T., SALESIN, D., AND STUETZLE, W. Interactive Multiresolution Surface Viewing. Proceedings of SIGGRAPH 96 (1996), 91-98. 
    3. CIGNONI, P., ROCCHINI, C., AND SCOPIGNO, R. Metro: Measuring Error on Simplified Surfaces. Computer Graphics Forum 17, 2 (1998), 167-174.
    4. COHEN-OR, D., LEVIN, D., AND REMEZ, O. Progressive Compression of Arbitrary Triangular Meshes. IEEE Visualization ’99 (1999), 67-72. 
    5. DAVIS, G., AND CHAWLA, S. Image Coding Using Optimized Significance Tree Quantization. In Prodeedings Data Compression Conference, 387-396, 1997. 
    6. DAVIS, G., AND NOSRATINIA, A. Wavelet-based Image Coding: An Overview. Applied Computational Control, Signals, and Circuits 1, 1 (1998).
    7. DESBRUN, M., MEYER, M., SCHRÖDER, P., AND BARR, A. H. Implicit Fairing of Irregular Meshes Using Diffusion and Curvature Flow. Proceedings of SIGGRAPH 99 (1999), 317-324. 
    8. DEVORE, R. A., JAWERTH, B., AND LUCIER, B. J. Surface Compression. Computer Aided Geometric Design 9 (1992), 219-239. 
    9. DYN, N., LEVIN, D., AND GREGORY, J. A. A Butterfly Subdivision Scheme for Surface Interpolation with Tension Control. ACM Transactions on Graphics 9, 2 (1990), 160-169. 
    10. ECK, M., DEROSE, T., DUCHAMP, T., HOPPE, H., LOUNSBERY, M., AND STUETZLE, W. Multiresolution Analysis of Arbitrary Meshes. Proceedings of SIGGRAPH 95 (1995), 173-182. 
    11. GOLUB, G. H., AND LOAN, C. F. V. Matrix Computations, 2nd ed. The John Hopkins University Press, Baltimore, 1983. 
    12. GROSS, M. H., STAADT, O. G., AND GATTI, R. Efficient Triangular Surface Approximations Using Wavelets and Quadtree Data Structures. IEEE Transactions on Visualization and Computer Graphics 2, 2 (1996). 
    13. GUMHOLD, S., AND STRASSER, W. Real Time Compression of Triangle Mesh Connectivity. Proceedings of SIGGRAPH 98 (1998), 133-140. 
    14. GUSKOV, I., SWELDENS, W., AND SCHRÖDER, P. Multiresolution Signal Processing for Meshes. Proceedings of SIGGRAPH 99 (1999), 325-334. 
    15.  GUSKOV, I., VIDIMCE, K., SWELDENS, W., AND SCHRÖDER, P. Normal Meshes. Proceedings of SIGGRAPH 00 (2000). 
    16.  HOPPE, H. Efficient Implementation of Progressive Meshes. Computers & Graphics 22, 1 (1998), 27-36.
    17.  KING, D., AND ROSSIGNAC, J. Optimal Bit Allocation in 3D Compression. Tech. Rep. GIT-GVU-99-07, Georgia Institute of Technology, 1999.
    18.  KOBBELT, L., VORSATZ, J., LABSIK, U., AND SEIDEL, H.-P. A Shrink Wrapping Approach to Remeshing Polygonal Surfaces. Computer Graphics Forum 18 (1999), 119-130.
    19.  KOLAROV, K., AND LYNCH, W. Compression of Functions Defined on Surfaces of 3D Objects. In Proc. of Data Compression Conference, J. Storer and M. Cohn, Eds., 281-291, 1997. 
    20.  KRISHNAMURTHY, V., AND LEVOY, M. Fitting Smooth Surfaces to Dense Polygon Meshes. Proceedings of SIGGRAPH 96 (1996), 313-324. 
    21.  LEE, A. W. F., SWELDENS, W., SCHRÖDER, P., COWSAR, L., AND DOBKIN, D. MAPS: Multiresolution Adaptive Parameterization of Surfaces. Proceedings of SIGGRAPH 98 (1998), 95-104. 
    22.  LEVOY, M. The Digital Michelangelo Project. In Proceedings of the 2nd International Conference on 3D Digital Imaging and Modeling, October 1999. 
    23.  LI, J., AND KUO, C. Progressive Coding of 3-D Graphic Models. Proceedings of the IEEE 86, 6 (1998), 1052-1063.
    24.  LOOP, C. Smooth Subdivision Surfaces Based on Triangles. Master’s thesis, University of Utah, Department of Mathematics, 1987.
    25.  LOUNSBERY, M., DEROSE, T. D., AND WARREN, J. Multiresolution Analysis for Surfaces of Arbitrary Topological Type. ACM Transactions on Graphics 16, 1 (1997), 34-73. Originally available as TR-93-10-05, October, 1993, Department of Computer Science and Engineering, University of Washington. 
    26. PAJAROLA, R., AND ROSSIGNAC, J. Compressed Progressive Meshes. Tech. Rep. GIT-GVU-99-05, Georgia Institute of Technology, 1999.
    27.  RIEMENSCHNEIDER, S. D., AND SHEN, Z. Wavelets and Pre-Wavelets in Low Dimensions. J. Approx. Th. 71, 1 (1992), 18-38. 
    28.  ROSSIGNAC, J. Edgebreaker: Connectivity Compression for Triangle Meshes. IEEE Transactions on Visualization and Computer Graphics 5, 1 (1999), 47-61. 
    29.  ROSSIGNAC, J., AND SZYMCZAK, A. Wrap&Zip: Linear Decoding of Planar Triangle Graphs. Tech. Rep. GIT-GVU-99-08, Georgia Institute of Technology, 1999.
    30.  SAID, A., AND PEARLMAN, W. A New, Fast, and Efficient Image Codec Based on Set Partitioning in Hierarchical Trees. IEEE Transaction on Circuits and Systems for Video Technology 6, 3 (1996), 243-250. 
    31.  SCHRÖDER, P., AND SWELDENS, W. Spherical Wavelets: Efficiently Representing Functions on the Sphere. Proceedings of SIGGRAPH 95 (1995), 161- 172. 
    32.  SHAPIRO, J. Embedded Image-Coding using Zerotrees of Wavelet Coefficients. IEEE Transactions on Signal Processing 41, 12 (1993), 3445-3462.
    33.  STAADT, O. G., GROSS, M. H., AND WEBER, R. Multiresolution Compression And Reconstruction. IEEE Visualization ’97 (1997), 337-346. 
    34.  TAUBIN, G., GUEZIEC, A., HORN, W., AND LAZARUS, F. Progressive Forest Split Compression. Proceedings of SIGGRAPH 98 (1998), 123-132. 
    35.  TAUBIN, G., AND ROSSIGNAC, J. Geometric Compression Through Topological Surgery. ACM Transactions on Graphics 17, 2 (1998), 84-115. 
    36.  TAUBIN, G., AND ROSSIGNAC, J., Eds. 3D Geometry Compression. No. 21 in Course Notes. ACM Siggraph, 1999.
    37. TOUMA, C., AND GOTSMAN, C. Triangle Mesh Compression. Graphics Interface ’98 (1998), 26-34.
    38.  ZORIN, D., SCHRÖDER, P., AND SWELDENS, W. Interpolating Subdivision for Meshes with Arbitrary Topology. Proceedings of SIGGRAPH 96 (1996), 189-192. 
    39.  ZORIN, D., SCHRÖDER, P., AND SWELDENS, W. Interactive Multiresolution Mesh Editing. Proceedings of SIGGRAPH 97 (1997), 259-268. 

ACM Digital Library Publication:


Overview Page: