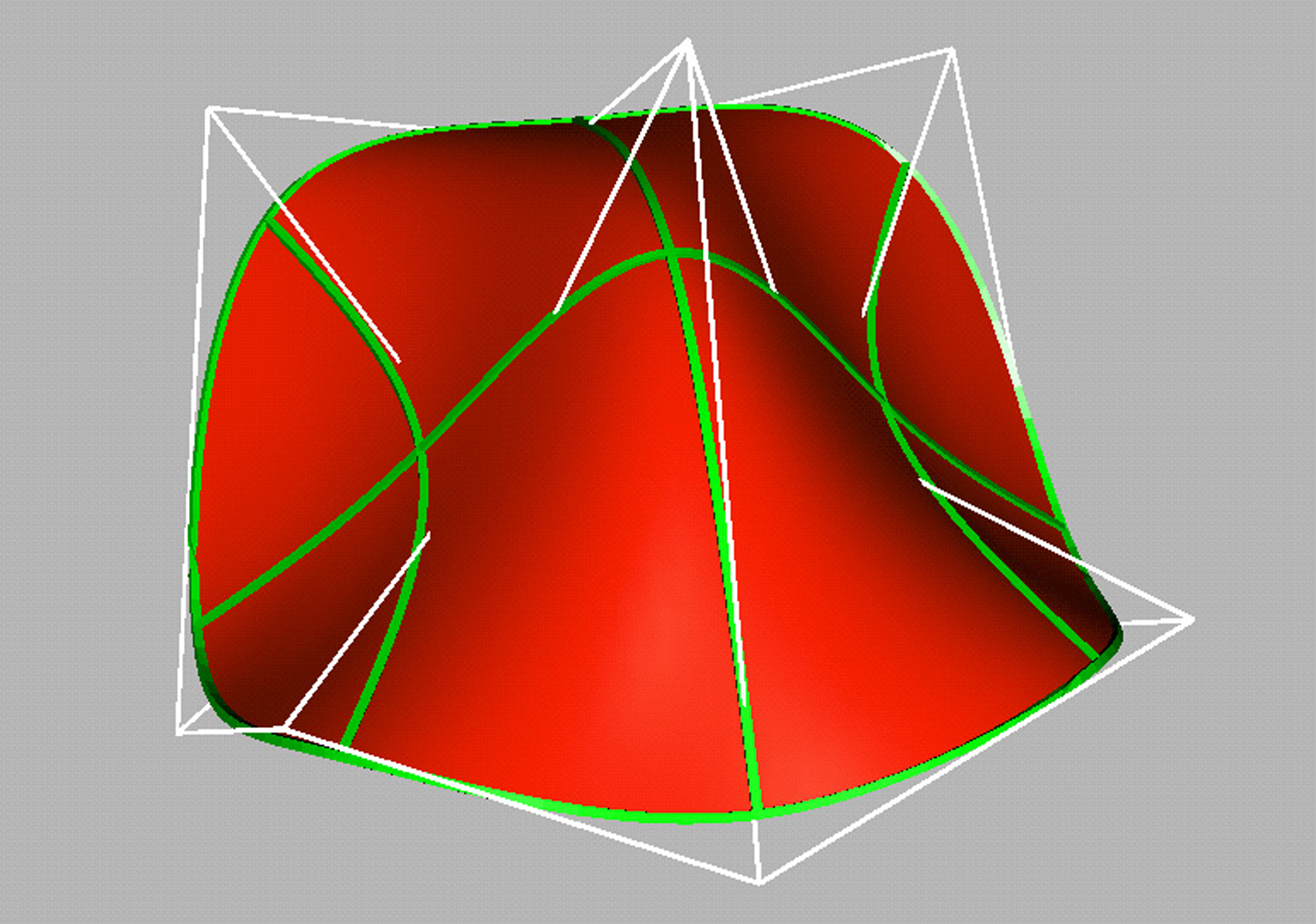
“Interpolating nets of curves by smooth subdivision surfaces” by Levin

A subdivision algorithm is presented for the computation and representation of a smooth surface of arbitrary topological type interpolating a given net of smooth curves. The algorithm belongs to a new class of subdivision schemes called combined subdivision schemes. These schemes can exactly interpolate a net of curves given in any parametric representation. The surfaces generated by our algorithm are G2 except at a finite number of points, where the surface is G1 and has bounded curvature. The algorithm is simple and easy to implement, and is based on a variant of the famous Catmull-Clark subdivision scheme.

1. E. Catmull and J. Clark. Recursively generated b-spline surfaces on arbitrary topological meshes. Computer Aided Design, 10:350-355, 1978.
2. T. DeRose, M. Kass, and T. Truong. Subdivision surfaces in character animation. In SIGGRAPH 98 Conference Proceedings, Annual Conference Series, pages 85-94. ACM SIG- GRAPH, 1998.
3. D. Doo and M. Sabin. Behaviour of recursive division surface near extraordinary points. Computer Aided Design, 10:356- 360, 1978.
4. N. Dyn, J. A. Greogory, and D. Levin. A butterfly subdivision scheme for surface interpolation with tension control. A CM Transactions on Graphics, 9:160-169, 1990.
5. M. Halstead, M. Kass, and T. DeRose. Efficient, fair interpolation using catmull-clark surfaces. In SIGGRAPH 93 Conference Proceedings, Annual Conference Series, pages 35-44. ACM SIGGRAPH, 1993.
6. L. Kobbelt, T. Hesse, H. Prautzsch, and K. Schweizerhof. Interpolatory subdivision on open quadrilateral nets with arbitrary topology. Computer Graphics Forum, 15:409-420, 1996. Eurographics ’96 issue.
7. A. Levin. Analysis of combined subdivision schemes 1. in preparation, available on the web at http://www.math.tau.ac.il/-adilev, 1999.
8. A. Levin. Analysis of combined subdivision schemes 2. in preparation, available on the web at http://www.math.tau.ac.il/-adilev, 1999.
9. A. Levin. Analysis of combined subdivision schemes for the interpoation of curves. SIGGRAPH’99 CDROM Proceedings, 1999.
10. A. Levin. Combined subdivision schemes for the design of surfaces satisfying boundary conditions. To appear in CAGD, 1999.
11. C. Loop. Smooth spline surfaces based on triangles. Master’s thesis, University of Utah, Department of Mathematics, 1987.
12. A. H. Nasri. Curve interpolation in recursively generated bspline surfaces over arbitrary topology. Computer Aided Geometric Design, 14:No 1, 1997.
13. A. H. Nasri. Interpolation of open curves by recursive subdivision surface. In T. Goodman and R. Martin, editors, The Mathematics of Surfaces VII, pages 173-188. Information Geometers, 1997.
14. M. Sabin. Cubic recursive division with bounded curvature. In E J. Laurent, A. le Mehaute, and L. L. Schumaker, editors, Curves and Surfaces, pages 411-4 14. Academic Press, 1991.
15. J. Schweitzer. Analysis and Applications of Subdivision Surfaces. PhD thesis, University of Washington, Seattle, 1996.
16. D. J. T. Storry and A. A. Ball. Design of an n-sided surface patch. Computer Aided Geometric Design, 6:111-120, 1989.
17. G. Taubin. A signal processing approach to fair surface design. In Robert Cook, editor, SIGGRAPH 95 Conference Proceedings, Annual Conference Series, pages 351-358. ACM SIGGRAPH, Addison Wesley, August 1995. held in Los Angeles, California, 06-11 August 1995.
18. D. Zorin, P. Schr6der, and W. Sweldens. Interpolating subdivision for meshes with arbitrary topology. Computer Graphics Proceedings (SIGGRAPH 96), pages 189-192, 1996.