“Fair morse functions for extracting the topological structure of a surface mesh” by Ni, Garland and Hart

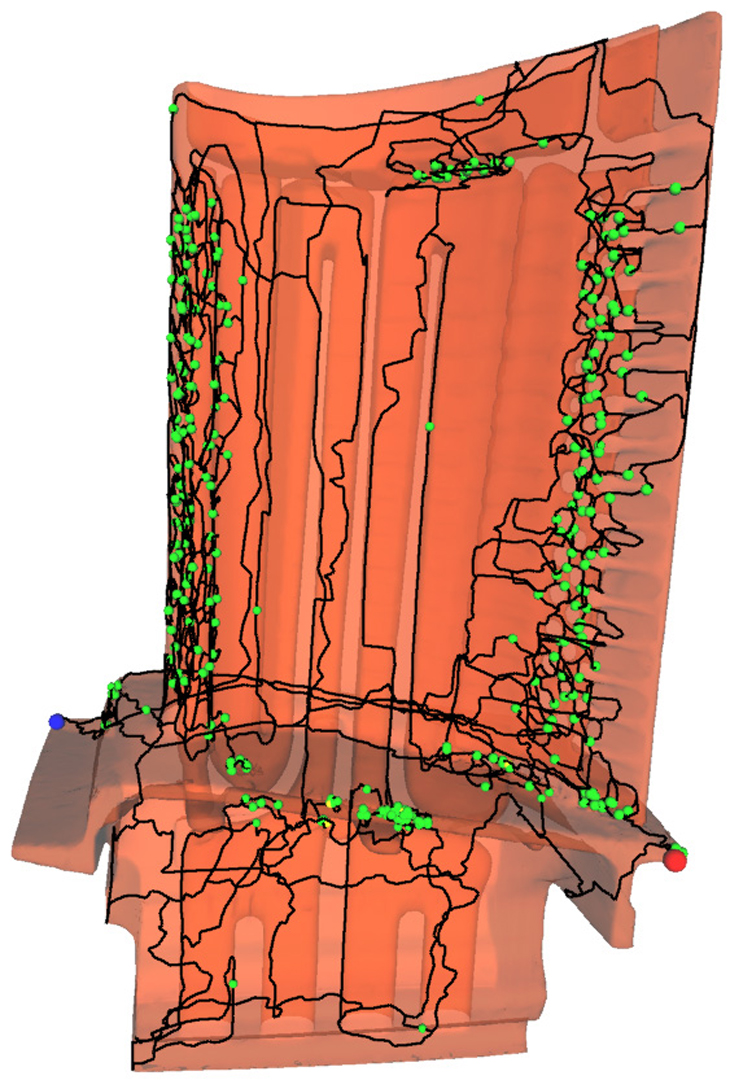
Morse theory reveals the topological structure of a shape based on the critical points of a real function over the shape. A poor choice of this real function can lead to a complex configuration of an unnecessarily high number of critical points. This paper solves a relaxed form of Laplace’s equation to find a “fair” Morse function with a user-controlled number and configuration of critical points. When the number is minimal, the resulting Morse complex cuts the shape into a disk. Specifying additional critical points at surface features yields a base domain that better represents the geometry and shares the same topology as the original mesh, and can also cluster a mesh into approximately developable patches. We make Morse theory on meshes more robust with teflon saddles and flat edge collapses, and devise a new “intermediate value propagation” multigrid solver for finding fair Morse functions that runs in provably linear time.

1. AKSOYLU, B., KHODAKOVSKY, A., AND SCHROEDER, P. 2003. Multilevel solvers for unstructured surface meshes. Siam J. Sci. Comput. (in review). Google ScholarDigital Library
2. AXEN, U., AND EDELSBRUNNER, H. 1998. Auditory morse analysis of triangulated manifolds. In Mathematical Visualization, H.-C. Hege and K. Polthier, Eds. Springer-Verlag, Heidelberg, 223–236.Google Scholar
3. BAJAJ, C. L., AND SCHIKORE, D. R. 1998. Topology preserving data simplification with error bounds. Computers and Graphics 22, 1, 3–12.Google ScholarCross Ref
4. BAJAJ, C. L., PASCUCCI, V., AND SCHIKORE, D. 1998. Visualization of scalar topology for structural enhancement. IEEE Visualization ’98, 51–58. Google ScholarDigital Library
5. BANCHOFF, T. F. 1970. Critical points and curvature for embedded polyhedral surfaces. American Mathematical Monthly 77, 475–485.Google ScholarCross Ref
6. BOLZ, J., FARMER, I., GRINSPUN, E., AND SCHRÖDER, P. 2003. Sparse matrix solvers on the GPU: Conjugate gradients and multigrid. ACM Trans. on Graphics 22, 3 (July), 912–924. (Proc. SIGGRAPH 2003). Google ScholarDigital Library
7. BREMER, P.-T., EDELSBRUNNER, H., HAMANN, B., AND PASCUCCI, V. 2003. A multi-resolution data structure for two-dimensional Morse-Smale functions. Proc. Visualization 03, 139–146. Google ScholarDigital Library
8. CHUNG, F. R. K. 1997. Spectral Graph Theory. American Mathematical Society.Google Scholar
9. DE VERDIÈRE, E. C., AND LAZARUS, F. 2002. Optimal system of loops on an orientable surface. Proc. Foundations of CS, 627–636. Google ScholarDigital Library
10. DESBRUN, M., MEYER, M., SCHROEDER, P., AND BARR, A. H. 1999. Implicit fairing of irregular meshes using diffusion and curvature flow. Proc. SIGGRAPH 99, 317–324. Google ScholarDigital Library
11. DESBRUN, M., MEYER, M., AND ALLIEZ, P. 2002. Intrinsic parameterizations of surface meshes. Computer Graphics Forum 21 (Sep.), 209–218. (Proc. Eurographics 2002).Google ScholarCross Ref
12. DEY, T. K., AND SCHIPPER, H. 1995. A new technique to compute polygonal schema for 2-manifolds with application to null-homotopy detection. Discrete and Computational Geometry 14, 93–110.Google ScholarDigital Library
13. DEY, T. K., EDELSBRUNNER, H., AND GUHA, S. 1999. Computational topology. In Advances in Discrete and Computational Geometry, B. Chazelle, J. Goodman, and R. Pollack, Eds. Providence.Google Scholar
14. DEY, T. K., EDELSBRUNNER, H., GUHA, S., AND NEKHAYEV, D. 1999. Topology preserving edge contraction. Publ. Inst. Math. (Beograd) (N.S.) 66, 23–45. Also Tech Report RGI-Tech-98-018, Raindrop Geomagic Inc., 1998.Google Scholar
15. DOBKIN, D., AND KIRKAPATRICK, D. 1985. A linear algorithm for determining the separation of convex polyghedra. J. of Algorithms 6, 381–392.Google ScholarCross Ref
16. EDELSBRUNNER, H., LETSCHER, D., AND ZOMORODIAN, A. 2002. Topological persistence and simplification. Discrete and Computational Geometry 28, 4, 511–533.Google ScholarDigital Library
17. EDELBRUNNER, H., HARER, J., NATARAJAN, V., AND PASCUCCI, V. 2003. Morse-Smale complexes for piecewise linear 3-manifolds. Proc. Symp. on Computational Geometry, 361–370. Google ScholarDigital Library
18. EDELSBRUNNER, H., HARER, J., AND ZOMORODIAN, A. 2003. Hierarchical Morse-Smale complexes for piecewise linear 2-manifolds. Discrete and Computational Geometry 30, 1, 87–107.Google ScholarCross Ref
19. ERICKSON, J., AND HAR-PELED, S. 2002. Optimally cutting a surface into a disk. Proc. ACM Symp. on Comp. Geom., 244–253. Google ScholarDigital Library
20. FIRBY, P., AND GARDINER, C. 1991. Surface Topology, 2nd ed. Ellis Horwood.Google Scholar
21. FLOATER, M. 1997. Parameterization and smooth approximation of surface triangulations. Computer-Aided Geometric Design 14, 4, 231–250. Google ScholarDigital Library
22. FLOATER, M. S. 2003. Mean value coordinates. Computer-Aided Geometric Design 20, 1 (Mar.), 19–27. Google ScholarDigital Library
23. GARLAND, M., AND HECKBERT, P. S. 1997. Surface simplification using quadric error metrics. Proc. SIGGRAPH 97, 209–216. Google ScholarDigital Library
24. GU, X., GORTLER, S. J., AND HOPPE, H. 2002. Geometry images. ACM Trans. on Graphics (Proc. SIGGRAPH 2002) 21, 3 (July), 355–361. Google ScholarDigital Library
25. GUSKOV, I., AND WOOD, Z. 2001. Topological noise removal. Proc. Graphics Interface, 19–26. Google ScholarDigital Library
26. HACKBUSCH, W. 1985. Multi-Grid Methods and Applications. Springer-Verlag.Google Scholar
27. HILAGA, M., SHINAGAWA, Y., KOHMURA, T., AND KUNII, T. L. 2001. Topology matching for fully automatic similarity estimation of 3D shapes. Proc. SIGGRAPH 2001, 203–212. Google ScholarDigital Library
28. KARTASHEVA, E. 1999. The algorithm for automatic cutting of three-dimensional polyhedrons of h-genus. Proc. Shape Modeling Intl. 99, 26–33. Google ScholarDigital Library
29. KOBBELT, L., CAMPAGNA, S., VORSATZ, J., AND SEIDEL, H.-P. 1998. Interactive multi-resolution modeling on arbitrary meshes. Proc. SIGGRAPH 98, 105–114. Google ScholarDigital Library
30. LAZARUS, F., POCCHIOLA, M., VEGTER, G., AND VERROUST, A. 2001. Computing a canonical polygonal schema of an orientable triangulated surface. ACM Symp. on Comp. Geom., 80–89. Google ScholarDigital Library
31. LEE, A. W. F., SWELDENS, W., SCHROEDER, P., COWSAR, L., AND DOBKIN, D. 1998. MAPS: multiresolution adaptive parameterization of surfaces. Proc. SIGGRAPH 98, 95–104. Google ScholarDigital Library
32. LEE, A. W. F., DOBKIN, D., SWELDENS, W., AND SCHRÖDER, P. 1999. Multiresolution mesh morphing. Proc. SIGGRAPH 99, 343–350. Google ScholarDigital Library
33. MILNOR, J. 1963. Morse Theory. Princeton Univ. Press.Google Scholar
34. MISCHAIKOW, K., AND MROZEK, M. 2002. Conley index. In Handbook of dynamical systems, Vol. 2. North-Holland, 393–460.Google Scholar
35. MISCHAIKOW, K. 1995. Conley index theory. In Dynamical systems (Montecatini Terme, 1994), vol. 1609 of Lecture Notes in Math. Springer, 119–207.Google Scholar
36. NACKMAN, L. 1984. Two-dimensional critical point configuration graphs. IEEE Trans. PAMI 6, 442–450.Google Scholar
37. PINKALL, U., AND POLTHIER, K. 1993. Computing discrete minimal surfaces and their conjugates. Experimental Mathematics 2, 1, 15–36.Google ScholarCross Ref
38. PIPONI, G., AND BORSHUKOV, D. 2000. Seamless texture mapping of subdivision surfaces by model pelting and texture blending. Proc. SIGGRAPH 2000, 471–478. Google ScholarDigital Library
39. RAY, N., AND LEVY, B. 2003. Hierarchical least squares conformal map. Proc. Pacific Graphics, 263–270. Google ScholarDigital Library
40. SANDER, P. V., WOOD, Z. J., GORTLER, S. J., SNYDER, J., AND HOPPE, H. 2003. Multi-chart geometry images. Proc. Symp. Geom. Proc., 146–155. Google ScholarDigital Library
41. SHEFFER, A., AND DE STURLER, E. 2002. Surface parameterization for meshing by triangulation flattening. ACM Trans. on Graphics 21, 4, 874–890. Google ScholarDigital Library
42. SHEFFER, A., AND HART, J. C. 2002. Seamster: inconspicuous low-distortion texture seam layout. Proc. Visualization ’02, 291–298. Google ScholarDigital Library
43. SHINAGAWA, Y., KUNII, T. L., AND KERGOSIEN, Y. L. 1991. Surface coding based on morse theory. IEEE Computer Graphics & Applications 11, 5, 66–78. Google ScholarDigital Library
44. STANDER, B. T., AND HART, J. C. 1997. Guaranteeing the topology of an implicit surface polygonization for interactive modeling. Proc. SIGGRAPH 97, 279–286. Google ScholarDigital Library
45. STEINER, D., AND FISCHER, A. 2001. Topology recognition of 3D closed freeform objects based on topological graphs. Proc. Pacific Graphics (Oct.), 82–88. Google ScholarDigital Library
46. TAUBIN, G. 1995. A signal processing approach to fair surface design. Proc. SIGGRAPH 95, 351–358. Google ScholarDigital Library
47. VEGTER, G. 1997. Computational topology. In Handbook of Discrete and Computational Geometry. CRC Press, 517–536. Google ScholarDigital Library
48. ZHANG, E., MISCHAIKOW, K., AND TURK, G. 2003. Feature-based surface parameterization and texture mapping. Tech. Rep. GVU 03–29, Georgia Tech.Google Scholar