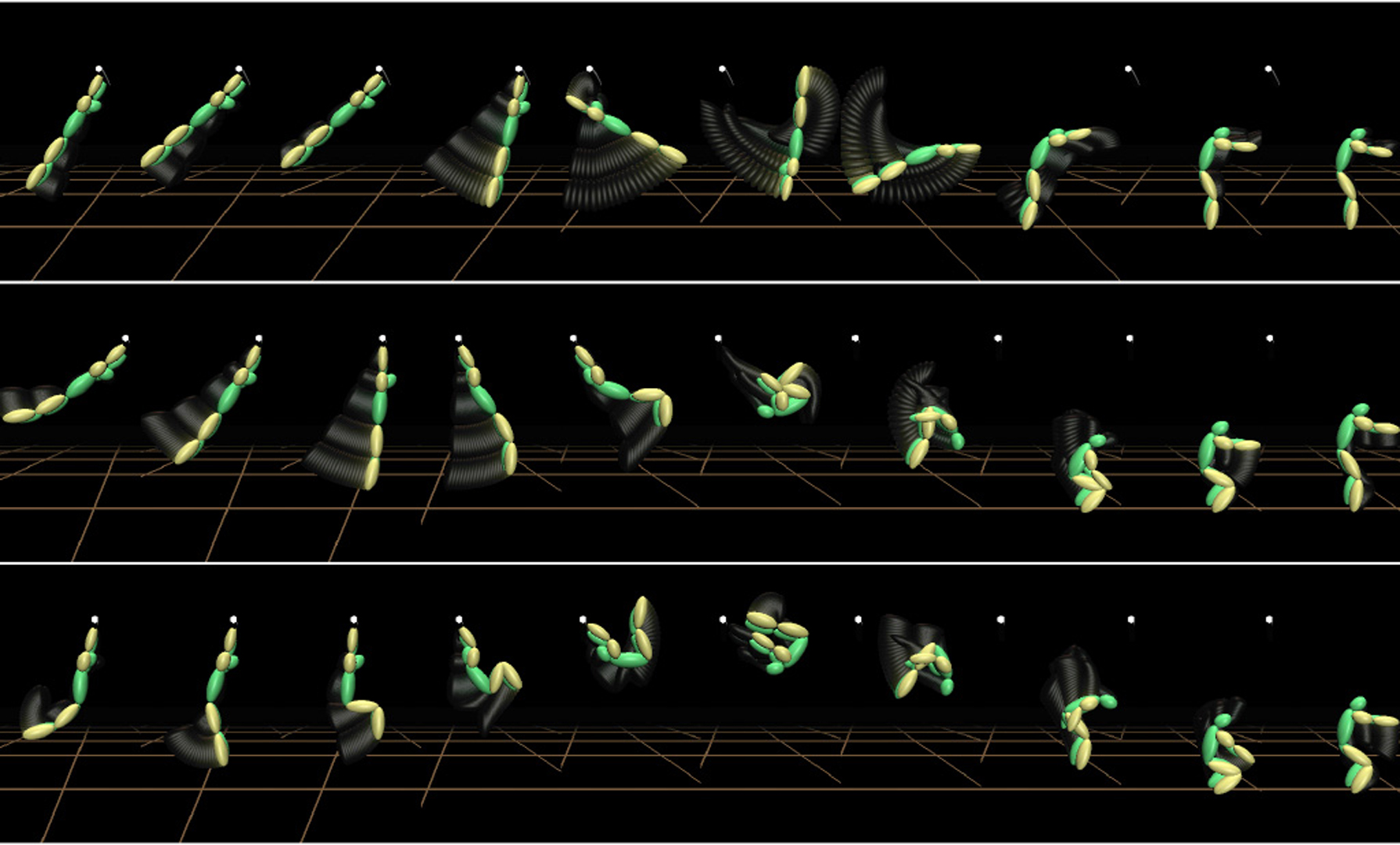
“Efficient synthesis of physically valid human motion” by Fang and Pollard

Optimization is a promising way to generate new animations from a minimal amount of input data. Physically based optimization techniques, however, are difficult to scale to complex animated characters, in part because evaluating and differentiating physical quantities becomes prohibitively slow. Traditional approaches often require optimizing or constraining parameters involving joint torques; obtaining first derivatives for these parameters is generally an O(D2) process, where D is the number of degrees of freedom of the character. In this paper, we describe a set of objective functions and constraints that lead to linear time analytical first derivatives. The surprising finding is that this set includes constraints on physical validity, such as ground contact constraints. Considering only constraints and objective functions that lead to linear time first derivatives results in fast per-iteration computation times and an optimization problem that appears to scale well to more complex characters. We show that qualities such as squash-and-stretch that are expected from physically based optimization result from our approach. Our animation system is particularly useful for synthesizing highly dynamic motions, and we show examples of swinging and leaping motions for characters having from 7 to 22 degrees of freedom.

1. ALBRO, J. V., SOHL, G. A., AND BOBROW, J. E. 2000. On the computation of optimal high-dives. In Proc. IEEE Intl. Conference on Robotics and Automation.Google ScholarCross Ref
2. ARIKAN, O., AND FORSYTH, D. A. 2002. Interactive motion generation from examples. ACM Transactions on Graphics 21, 3 (July), 483–490. Google ScholarDigital Library
3. BROTMAN, L. S., AND NETRAVALI, A. N. 1988. Motion interpolation by optimal control. In Computer Graphics (Proceedings of SIGGRAPH 88), vol. 22, 309–315. Google Scholar
4. COHEN, M. F. 1992. Interactive spacetime control for animation. In Computer Graphics (Proceedings of SIGGRAPH 92), vol. 26, 293–302. Google Scholar
5. CONN, A. R., GOULD, N. I. M., AND TOINT, P. L. 1992. LANCELOT: a Fortran package for large-scale nonlinear optimization (Release A). No. 17 in Springer Series in Computational Mathematics. Springer Verlag, Heidelberg, Berlin, New York. Google Scholar
6. CRAWFORD, L. S. 1998. Learning Control of Complex Skills. PhD Thesis, UC Berkeley. Google Scholar
7. DASGUPTA, A., AND NAKAMURA, Y. 1999. Making feasible walking motion of humanoid robots from human motion capture data. In Proc. IEEE Intl. Conference on Robotics and Automation.Google Scholar
8. FEATHERSTONE, R. 1987. Robot Dynamics Algorithms. Kluwer Academic Publishers, Boston, MA. Google Scholar
9. GLEICHER, M. 1997. Motion editing with spacetime constraints. In Proceedings of the 1997 Symposium on Interactive 3D Graphics, 139–148. Google Scholar
10. GRZESZCZUK, R., TERZOPOULOS, D., AND HINTON, G. 1998. Neuroanimator: Fast neural network emulation and control of physics-based models. In Proceedings of SIGGRAPH 98, Computer Graphics Proceedings, Annual Conference Series, 9–20. Google Scholar
11. KO, H., AND BADLER, N. I. 1996. Animating human locomotion with inverse dynamics. IEEE Computer Graphics and Applications (March), 50–59. Google Scholar
12. LEE, J., AND SHIN, S. Y. 1999. A hierarchical approach to interactive motion editing for human-like figures. In Proceedings of SIGGRAPH 99, Computer Graphics Proceedings, Annual Conference Series, 39–48. Google Scholar
13. LIU, Z., AND COHEN, M. 1994. Decomposition of linked gure motion: Diving. In 5th Eurographics Workshop on Animation and Simulation.Google Scholar
14. LIU, Z., AND COHEN, M. F. 1995. Keyframe motion optimization by relaxing speed and timing. In 6th Eurographics Workshop on Animation and Simulation.Google Scholar
15. LIU, C. K., AND POPOVIĆ, Z. 2002. Synthesis of complex dynamic character motion from simple animations. ACM Transactions on Graphics 21, 3 (July), 408–416. Google ScholarDigital Library
16. LIU, Z., GORTLER, S. J., AND COHEN, M. F. 1994. Hierarchical space-time control. In Proceedings of SIGGRAPH 94, Computer Graphics Proceedings, Annual Conference Series, 35–42. Google Scholar
17. LIU, Z. 1996. Efficient Animation Techniques Balancing Both User Control and Physical Realism. PhD thesis, Princeton University. Google Scholar
18. LO, J., AND METAXAS, D. 1999. Recursive dynamics and optimal control techniques for human motion planning. In Proceedings of Computer Animation ’99, 220–234. Google Scholar
19. NAGASAKA, K., INOUE, H., AND INABA, M. 1999. Dynamic walking pattern generation for a humanoid robot based on optimal gradient method. In Proc. IEEE Intl. Conference on Systems, Man, and Cybernetics, 908–913.Google Scholar
20. PANDY, M. G., AND ANDERSON, F. C. 2000. Dynamic simulation of human movement using large-scale models of the body. In Proc. IEEE Intl. Conference on Robotics and Automation.Google ScholarCross Ref
21. POLLARD, N. S., AND REITSMA, P. S. A. 2001. Animation of humanlike characters: Dynamic motion filtering with a physically plausible contact model. In Yale Workshop on Adaptive and Learning Systems.Google Scholar
22. POPOVIĆ, Z., AND WITKIN, A. P. 1999. Physically based motion transformation. In Proceedings of SIGGRAPH 99, Computer Graphics Proceedings, Annual Conference Series, 11–20. Google Scholar
23. POPOVIĆ, J., SEITZ, S. M., ERDMANN, M., POPOVIĆ, Z., AND WITKIN, A. P. 2000. Interactive manipulation of rigid body simulations. In Proceedings of SIGGRAPH 00, Computer Graphics Proceedings, Annual Conference Series, 209–218. Google ScholarDigital Library
24. ROSE, C. F., GUENTER, B., BODENHEIMER, B., AND COHEN, M. F. 1996. Efficient generation of motion transitions using spacetime constraints. In Proceedings of SIGGRAPH 96, Computer Graphics Proceedings, Annual Conference Series, 147–154. Google Scholar
25. TAKANISHI, A., ISHIDA, M., YAMAZAKI, Y., AND KATO, I. 1985. The realization of dynamic walking by the biped walking robot WL-10RD. In Proc. Intl. Conference on Advanced Robotics, 459–466.Google Scholar
26. VANDE PANNE, M. 1997. From footprints to animation. Computer Graphics Forum 16, 4 (Oct.), 211–223.Google Scholar
27. VUKOBRATOVIĆ, M. 1970. On the stability of biped locomotion. IEEE Trans. Biomedical Engineering 17, 1, 25–36.Google ScholarCross Ref
28. WITKIN, A., AND KASS, M. 1988. Spacetime constraints. In Computer Graphics (Proceedings of SIGGRAPH 88), vol. 22, 159–168. Google Scholar
29. YAMANE, K., AND NAKAMURA, Y. 2000. Dynamics filter – concept and implementation of on-line motion generator for human figures. In Proc. IEEE Intl. Conference on Robotics and Automation.Google Scholar