“Efficient symbolic differentiation for graphics applications” by Guenter

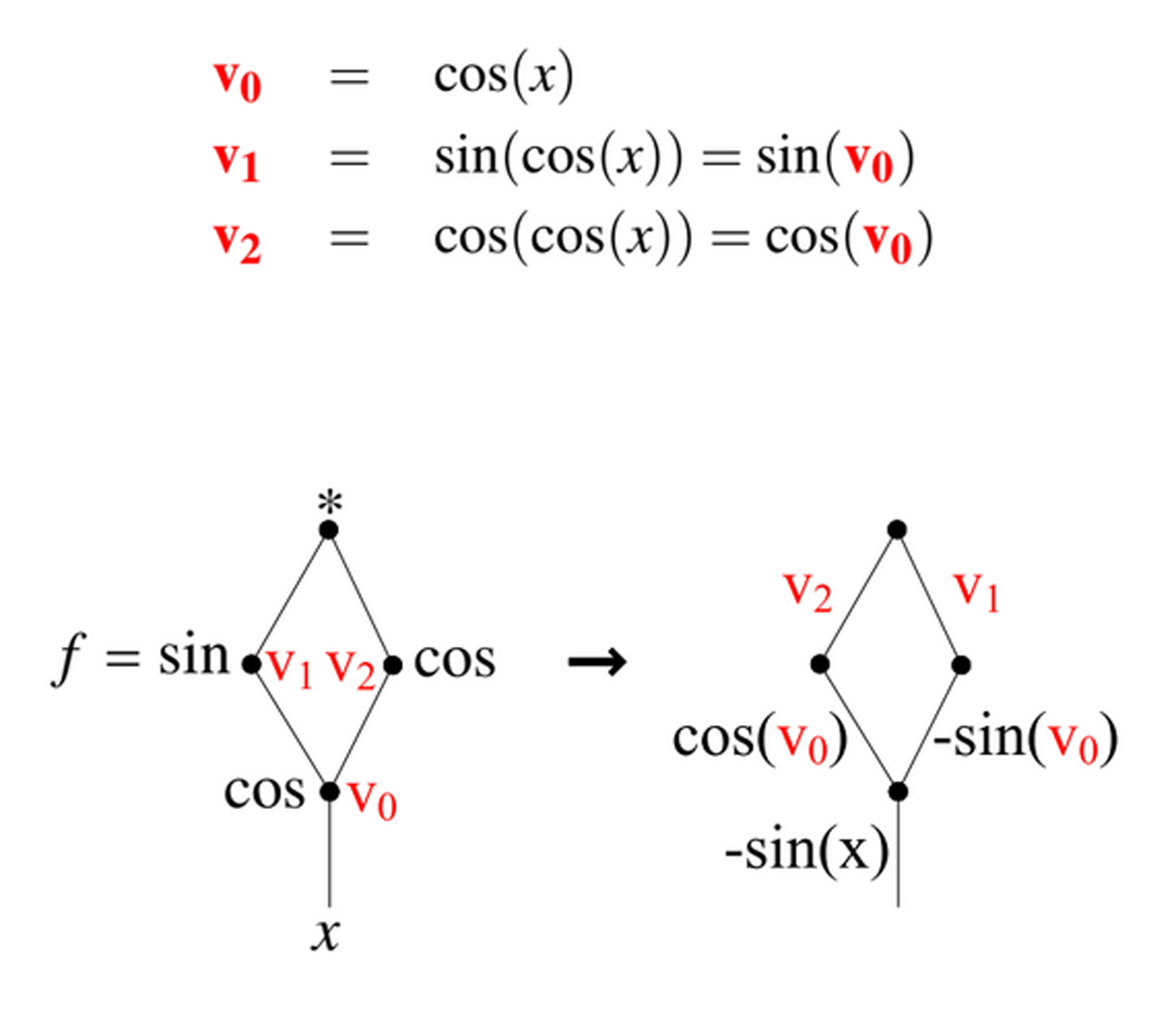
Functions with densely interconnected expression graphs, which arise in computer graphics applications such as dynamics, space-time optimization, and PRT, can be difficult to efficiently differentiate using existing symbolic or automatic differentiation techniques. Our new algorithm, D*, computes efficient symbolic derivatives for these functions by symbolically executing the expression graph at compile time to eliminate common subexpressions and by exploiting the special nature of the graph that represents the derivative of a function. This graph has a sum of products form; the new algorithm computes a factorization of this derivative graph along with an efficient grouping of product terms into subexpressions. For the problems in our test suite D* generates symbolic derivatives which are up to 4.6 x 103 times faster than those computed by the symbolic math program Mathematica and up to 2.2×105 times faster than the non-symbolic automatic differentiation program CppAD. In some cases the D* derivatives rival the best manually derived solutions.

1. Balafoutis, C. A., and Patel, R. V. 1991. Dynamic Analysis of Robot Manipulators: A Cartesion Tensor Approach. Kluwer Academic Publishers. Google ScholarDigital Library
2. Bauer, F. L. 1974. Computational graphs and rounding error. SIAM J. Numer. Anal. 11, 1, 87–96.Google ScholarDigital Library
3. Bischof, C. H., Carle, A., Khademi, P., and Mauer, A. 1996. ADIFOR 2.0: Automatic differentiation of Fortran 77 programs. IEEE Computational Science & Engineering 3, 3, 18–32. Google ScholarDigital Library
4. Bischof, C. H., Roh, L., and Mauer, A. 1997. ADIC — An extensible automatic differentiation tool for ANSI-C. Software–Practice and Experience 27, 12, 1427–1456. Google ScholarDigital Library
5. Cooper, K., Harvey, T., and Kennedy, K. 2001. A simple, fast dominance algorithm. Software Practice and Experience.Google Scholar
6. Fang, A. C., and Pollard, N. S. 2003. Efficient synthesis of physically valid human motion. ACM Transactions on Graphics 22, 3 (July), 417–426. Google ScholarDigital Library
7. Featherstone, R., and Orin, D. 2000. Robot dynamics: Equations and algorithms. Proc. IEEE Int. Conf. Robotics & Automation.Google Scholar
8. Griewank, A. 2000. Evaluating Derivatives: Principles and Techniques of Algorithmic Differentiation. Lecture Notes in Computer Science 120. Google ScholarDigital Library
9. Griewank, A. 2003. A mathematical view of automatic differentiation. In Acta Numerica, vol. 12. Cambridge University Press, 321–398.Google Scholar
10. Lee, S.-H., Kim, J., Park, F., Kim, M., and Bobrow, J. E. 2005. Newton-type algorithms for dynamics-based robot movement optimization. IEEE Trans. on robotics 21, 4, 657–667. Google ScholarDigital Library
11. Liu, Z., Gortler, S. J., and Cohen, M. F. 1994. Hierarchical spacetime control. Computer Graphics (SIGGRAPH 94 Proceedings), 35–42. Google ScholarDigital Library
12. Liu, C. K., Hertzmann, A., and Popovic, Z. 2005. Learning physics-based motion style with inverse optimization. ACM Transactions on Graphics (SIGGRAPH 2005). Google ScholarDigital Library
13. Martin, B., and Bobrow, J. 1997. Minimum effort motions for open chain manipulators with task dependent end-effector constraints.Google Scholar
14. Rall, L. B. 1981. Automatic Differentiation: Techniques and Applications. Springer Verlag.Google ScholarCross Ref
15. Sloan, P.-P., Luna, B., and Snyder, J. 2005. Local, de-formable precomputed radiance transfer. Computer Graphics Proceedings, Annual Conference Series, 1216–1224. Google ScholarDigital Library
16. Tadjouddine, E. M. 2007. Vertex ordering algorithms for jacobian computations using automatic differentiation. Submitted to the Computer Journal, Oxford University Press, March 2007.Google Scholar
17. van de Panne, M., Lazlo, J., and Fiume, E. L. 2000. Interactive control for physically-based animation. Computer Graphics (SIGGRAPH 2000 Proceedings), 201–208. Google ScholarDigital Library
18. Waters, R. C. 1979. Mechanical arm control. MIT Artificial Intelligence Lab Memo 549.Google Scholar
19. Witkin, A., and Kass, M. 1988. Spacetime constraints. Computer Graphics (SIGGRAPH 88 Proceedings) 22, 159–168. Google ScholarDigital Library