“Dual domain extrapolation” by Levy

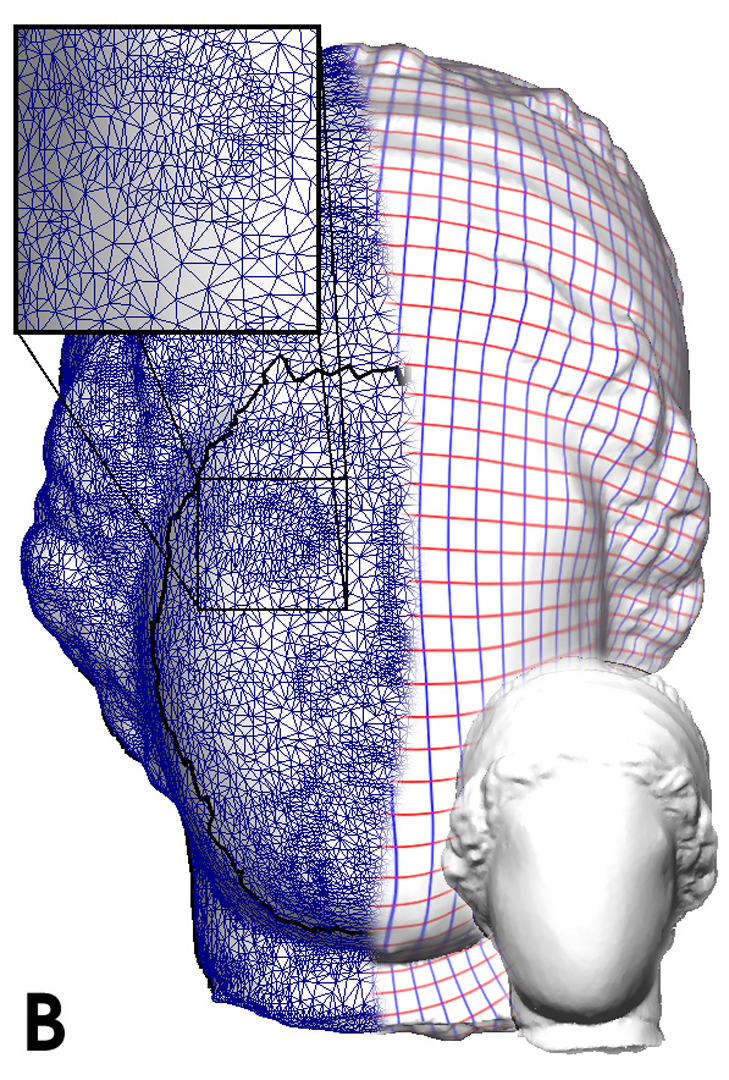
Shape optimization and surface fairing for polygon meshes have been active research areas for the last few years. Existing approaches either require the border of the surface to be fixed, or are only applicable to closed surfaces. In this paper, we propose a new approach, that computes natural boundaries. This makes it possible not only to smooth an existing geometry, but also to extrapolate its shape beyond the existing border. Our approach is based on a global parameterization of the surface and on a minimization of the squared curvatures, discretized on the edges of the surface. The so-constructed surface is an approximation of a minimal energy surface (MES). Using a global parameterization makes it possible to completely decouple the outer fairness (surface smoothness) from the inner fairness (mesh quality). In addition, the parameter space provides the user with a new means of controlling the shape of the surface. When used as a geometry filter, our approach computes a smoothed mesh that is discrete conformal to the original one. This allows smoothing textured meshes without introducing distortions.

1. ALLIEZ, P., MEYER, M., AND DESBRUN, M. 2002. Interactive Geometry Remeshing. ACM Transactions on Graphics (SIGGRAPH conf. proc.), 347–354. Google Scholar
2. BLOOR, M., AND WILSON, M. 1990. Using partial differential equations to generate free-form surfaces. Computer-Aided Design, 22, 202–212. Google ScholarDigital Library
3. BOISSONNAT, J.-D., AND CAZALS, F. 2002. Smooth surface reconstruction via natural neighbour interpolation of distance functions. Comp. Geometry Theory and Applications, 185–203. Google Scholar
4. BRAKKE, K. 1992. The surface evolver. Experimental Mathematics 1, 2, 141–165.Google ScholarCross Ref
5. BURCHARD, H., AYERS, J., FREY, W., AND SAPIDIS, N. 1994. Approximation with aesthetic constraints. In Designing Fair Curves and Surfaces, N. Sapidis, Ed., SIAM.Google Scholar
6. CARR, J. C., BEATSON, R. K., CHERRIE, J. B., MITCHELL, T. J., FRIGHT, W. R., MCCALLUM, B. C., AND EVANS, T. R. 2001. Reconstruction and representation of 3D objects with radial basis functions. In SIGGRAPH Conference Proceedings, 67–76. Google Scholar
7. CHOPP, D., AND SETHIAN, J. 1999. Motion by intrinsic Laplacian of curvature. Interfaces and Free Boundaries, 1, 1–18.Google Scholar
8. DESBRUN, M., MEYER, M., SCHRÖDER, P., AND BARR, A. 1999. Implicit fairing of irregular meshes using diffusion and curvature flow. In SIGGRAPH Conference Proceedings, ACM, 317–324. Google Scholar
9. DESBRUN, M., MEYER, M., AND ALLIEZ, P. 2002. Intrinsic parameterizations of surface meshes. In Proceedings of Eurographics, 209–218.Google Scholar
10. DO CARMO, M. 1976. Differential geometry of curves and surfaces. Prentice Hall, Englewood Cliffs, Inc.Google Scholar
11. FABRI, A., GIEZEMAN, G.-J., KETTNER, L., SCHIRRA, S., AND SCHÖNHERR, S. 2000. On the Design of CGAL, a Computational Geometry Algorithms Library. Softw. – Pract. Exp. 30, 11, 1167–1202. www.cgal.org. Google ScholarDigital Library
12. FLOATER, M. 1997. Parametrization and smooth approximation of surface triangulations. Computer Aided Geometric Design 14, 3 (April), 231–250. Google ScholarDigital Library
13. GUSKOV, I., SWELDENS, W., AND SCHRÖDER, P. 1999. Multiresolution signal processing for meshes. In SIGGRAPH Conference Proceedings, ACM, 325–334. Google Scholar
14. HORMANN, K., AND GREINER, G. 2000. MIPS: An efficient global parametrization method. In Curve and Surface Design: Saint-Malo 1999, P.-J. Laurent, P. Sablonnire, and L. Schumaker, Eds. Vanderbilt University Press, 153–162.Google Scholar
15. HSU, L., KUSNED, R., AND SULLIVAN, J. 1992. Minimizing the squared mean curvature integral for surfaces in space forms. Experimental Mathematics 1, 3, 191–207.Google ScholarCross Ref
16. KOBBELT, L., CAMPAGNA, S., VORSATZ, J., AND SEIDEL, H. 1998. Interactive multi-resolution modeling on arbitrary meshes. In SIGGRAPH Conference Proceedings, 105–114. Google Scholar
17. KOBBELT, L. 1997. Discrete fairing. In Proceedings of the Seventh IMA Conference on the Mathematics of Surfaces, 101–131.Google Scholar
18. LÉVY, B., PETITJEAN, S., RAY, N., AND MAILLOT, J. 2002. Least Squares Conformal Maps for Automatic Texture Atlas Generation. ACM Transactions on Graphics (SIGGRAPH conf. proc.), 362–371. Google Scholar
19. MALLET, J. 1992. Discrete Smooth Interpolation. Computer Aided Design 24, 4, 263–270.Google ScholarCross Ref
20. MORETON, H., AND SÉQUIN, C. 1992. Functional minimization for fair surface design. In SIGGRAPH Conference Proceedings, ACM. Google Scholar
21. MUSETH, K., BREEN, D. E., WHITAKER, R. T., AND BARR, A. H. 2002. Level set surface editing operators. ACM Transactions on Graphics (SIGGRAPH Conf. Proc.) 21, 3, 330–338. Google ScholarDigital Library
22. NOCEDAL, AND WRIGHT. 2000. Numerical Optimization. Springer.Google Scholar
23. OHTAKE, Y., BELYAEV, A., AND BOGAEVSKI, I. 2000. Polyhedral surface smoothing with simultaneous mesh regularization. In Geometric Modeling and Processing Proceedings, 229–237. Google ScholarCross Ref
24. PINKALL, U., AND POLTHIER, K. 1993. Computing discrete minimal surfaces and their conjugates. Experimental Math. 2, 15.Google ScholarCross Ref
25. SCHNEIDER, R., AND KOBBELT, L. Geometric fairing of irregular meshes for freeform surface design, to appear in the CAGD journal. Google Scholar
26. SCHNEIDER, R., AND KOBBELT, L. 2000. Generating fair meshes with G1 boundary conditions. In Geometric Modeling and Processing Proceedings, 251–261. Google Scholar
27. SHEFFER, A., AND DE STURLER, E. 2001. Parameterization of faceted surfaces for meshing using angle based attening. Engineering with Computers 17, 326–337.Google ScholarCross Ref
28. TAUBIN, G. 1995. A signal processing approach to fair surface design. In SIGGRAPH Conference Proceedings, ACM, 351–358. Google Scholar
29. WELCH, W., AND WITKIN, A. 1994. Free-form shape design using triangulated surfaces. In SIGGRAPH Conference Proceedings, ACM. Google Scholar