“Dihedral angle-based maps of tetrahedral meshes”
Conference:
Type(s):
Title:
- Dihedral angle-based maps of tetrahedral meshes
Session/Category Title: Simsquishal Geometry
Presenter(s)/Author(s):
Moderator(s):
Abstract:
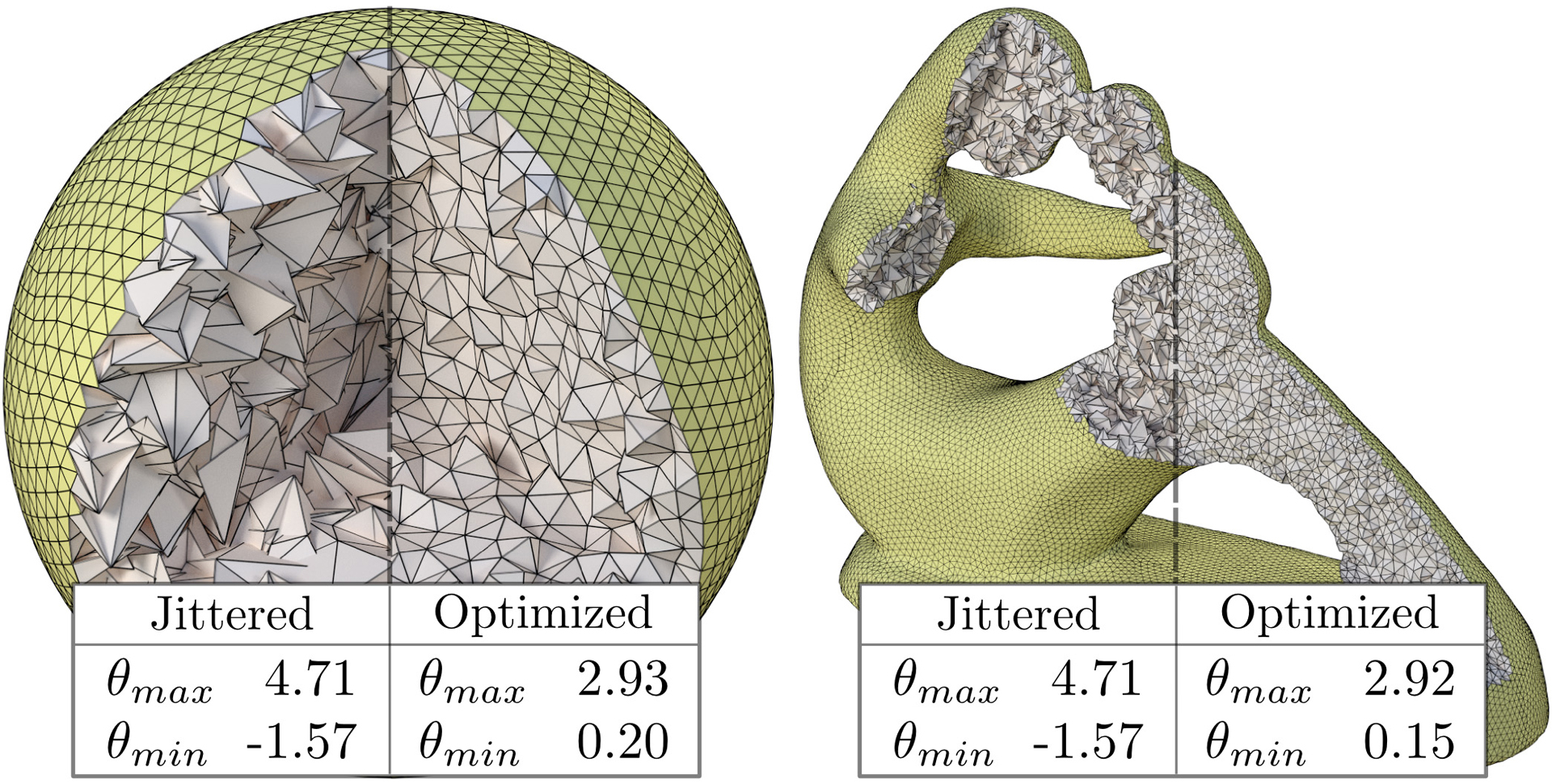
We present a geometric representation of a tetrahedral mesh that is solely based on dihedral angles. We first show that the shape of a tetrahedral mesh is completely defined by its dihedral angles. This proof leads to a set of angular constraints that must be satisfied for an immersion to exist in R3. This formulation lets us easily specify conditions to avoid inverted tetrahedra and multiply-covered vertices, thus leading to locally injective maps. We then present a constrained optimization method that modifies input angles when they do not satisfy constraints. Additionally, we develop a fast spectral reconstruction method to robustly recover positions from dihedral angles. We demonstrate the applicability of our representation with examples of volume parameterization, shape interpolation, mesh optimization, connectivity shapes, and mesh compression.
References:
1. Aigerman, N., and Lipman, Y. 2013. Injective and bounded distortion mappings in 3D. ACM Trans. Graph. 32, 4, 106:1–14. Google ScholarDigital Library
2. Alexa, M., Cohen-Or, D., and Levin, D. 2000. As-rigid-as-possible shape interpolation. In Proc. of SIGGRAPH ’00, 157–164. Google ScholarDigital Library
3. Arsigny, V., Fillard, P., Pennec, X., and Ayache, N. 2006. Log-Euclidean metrics for fast and simple calculus on diffusion tensors. Magnetic Resonance in Medicine 56, 2, 411–421.Google ScholarCross Ref
4. Barrett, J. W. 1994. First order Regge calculus. Classical and Quantum Gravity 11, 11, 2723–2730.Google ScholarCross Ref
5. Cervone, D. P. 1996. Tight immersions of simplicial surfaces in three space. Topology 35, 4, 863–873.Google ScholarCross Ref
6. Chen, Y., Davis, T. A., Hager, W. W., and Rajamanickam, S. 2008. Algorithm 887: CHOLMOD, supernodal sparse cholesky factorization and update/downdate. ACM Trans. Math. Softw. 35, 3, 22:1–14. Google ScholarDigital Library
7. Chen, R., Weber, O., Keren, D., and Ben-Chen, M. 2013. Planar shape interpolation with bounded distortion. ACM Trans. Graph. 32, 4, 108:1–12. Google ScholarDigital Library
8. Crane, K., Pinkall, U., and Schröder, P. 2011. Spin transformations of discrete surfaces. ACM Trans. Graph. 30, 4, 104:1–10. Google ScholarDigital Library
9. Crane, K., Pinkall, U., and Schröder, P. 2013. Robust fairing via conformal curvature flow. ACM Trans. Graph. 32, 4, 61:1–10. Google ScholarDigital Library
10. Di Battista, G., and Vismara, L. 1993. Angles of planar triangular graphs. In Proc. ACM Symp. on Theory of Computing (STOC), 431–437. Google ScholarDigital Library
11. Dittrich, B., and Speziale, S. 2008. Area-angle variables for general relativity. New Journal of Physics 10, 8, 083006.Google ScholarCross Ref
12. Graphite, 2015, Jan. http://alice.loria.fr.Google Scholar
13. Isenburg, M., Gumhold, S., and Gotsman, C. 2001. Connectivity shapes. In Proc. Conf. on Visualization (VIS), 135–142. Google ScholarDigital Library
14. Jiang, T., Huang, J., Wang, Y., Tong, Y., and Bao, H. 2014. Frame field singularity correction for automatic hexahedralization. IEEE Trans. Vis. Comput. Graphics 20, 8, 1189–1199. Google ScholarDigital Library
15. Ju, T., Schaefer, S., and Warren, J. 2005. Mean value coordinates for closed triangular meshes. ACM Trans. Graph. 24, 3, 561–566. Google ScholarDigital Library
16. Kircher, S., and Garland, M. 2008. Free-form motion processing. ACM Trans. Graph. 27, 2, 12:1–13. Google ScholarDigital Library
17. Labelle, F., and Shewchuk, J. R. 2007. Isosurface stuffing: Fast tetrahedral meshes with good dihedral angles. ACM Trans. Graph. 26, 3, 57:1–10. Google ScholarDigital Library
18. Levi, Z., and Gotsman, C. 2015. Smooth rotation enhanced as-rigid-as-possible mesh animation. IEEE Trans. Vis. Comput. Graphics 21, 2, 264–277.Google ScholarCross Ref
19. Li, Y., Liu, Y., Xu, W., Wang, W., and Guo, B. 2012. All-hex meshing using singularity-restricted field. ACM Trans. Graph. 31, 6, 177:1–11. Google ScholarDigital Library
20. Liu, Y., Wang, W., Lévy, B., Sun, F., Yan, D.-M., Lu, L., and Yang, C. 2009. On centroidal voronoi tessellation – energy smoothness and fast computation. ACM Trans. Graph. 28, 4, 101:1–17. Google ScholarDigital Library
21. Livesu, M., Vining, N., Sheffer, A., Gregson, J., and Scateni, R. 2013. Polycut: Monotone graph-cuts for polycube base-complex construction. ACM Trans. Graph. 32, 6, 171:1–12. Google ScholarDigital Library
22. Luo, F. 1997. On a problem of Fenchel. Geometriae Dedicata 64, 3, 277–282.Google ScholarCross Ref
23. Maglo, A., Lavoué, G., Dupont, F., and Hudelot, C. 2015. 3D mesh compression: Survey, comparisons, and emerging trends. ACM Comput. Surv. 47, 3, 44:1–44:41. Google ScholarDigital Library
24. Mullen, P., Tong, Y., Alliez, P., and Desbrun, M. 2008. Spectral conformal parameterization. Comput. Graph. Forum 27, 5, 1487–1494. Google ScholarDigital Library
25. Pentland, A., and Williams, J. R. 1989. Good vibrations: Modal dynamics for graphics and animation. ACM Trans. Graph. 23, 3, 207–214. Google ScholarDigital Library
26. Petersen, K. B., and Pedersen, M. S. 2012. The Matrix Cookbook. Technical University of Denmark.Google Scholar
27. Regge, T. 1961. General relativity without coordinates. Nuovo Cim. 19, 3, 558–571.Google ScholarCross Ref
28. Sheffer, A., and de Sturler, E. 2001. Parameterization of faceted surfaces for meshing using angle-based flattening. Engineering with Computers 17, 3, 326–337.Google ScholarCross Ref
29. Sheffer, A., Lévy, B., Mogilnitsky, M., and Bogomyakov, A. 2005. ABF++: fast and robust angle based flattening. ACM Trans. Graph. 24, 2, 311–330. Google ScholarDigital Library
30. Shewchuk, J. R., 2013. Lecture notes on geometric robustness. University of California at Berkeley.Google Scholar
31. Si, H., 2007. TetGen. A quality tetrahedral mesh generator and three-dimensional Delaunay triangulator. http://tetgen.berlios.de.Google Scholar
32. Springborn, B., Schröder, P., and Pinkall, U. 2008. Conformal equivalence of triangle meshes. ACM Trans. Graph. 27, 3, 77:1–11. Google ScholarDigital Library
33. Yin, X., Jin, M., Luo, F., and Gu, X. 2008. Discrete curvature flow for hyperbolic 3-manifolds with complete geodesic boundaries. In International Symp. on Visual Computing (ISVC).Google Scholar
34. Zayer, R., Rössl, C., and Seidel, H.-P. 2005. Variations on angle based flattening. In Advances in Multiresolution for Geometric Modelling, 187–199.Google Scholar
35. Zayer, R., Lévy, B., and Seidel, H.-P. 2007. Linear angle based parameterization. In Proc. EG/ACM Symp. on Geometry Processing (SGP), 135–141. Google ScholarDigital Library