“Digital Papercutting”

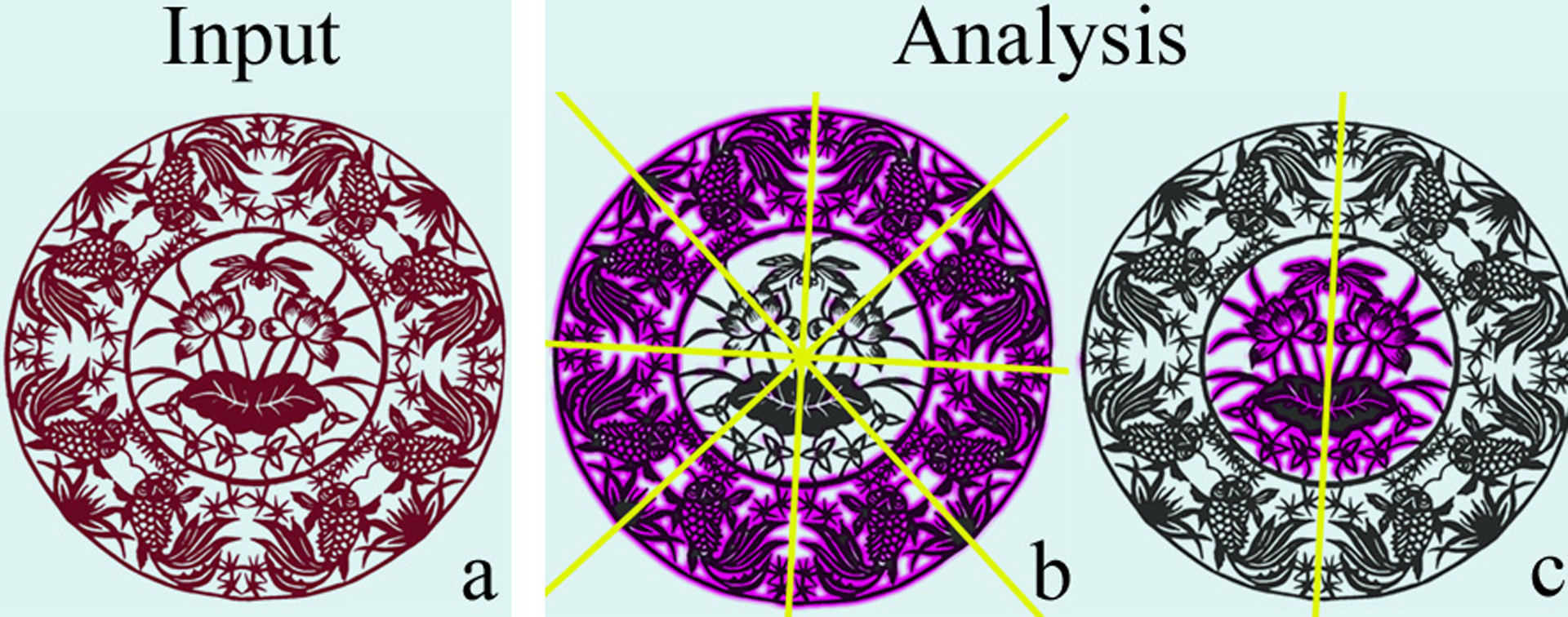
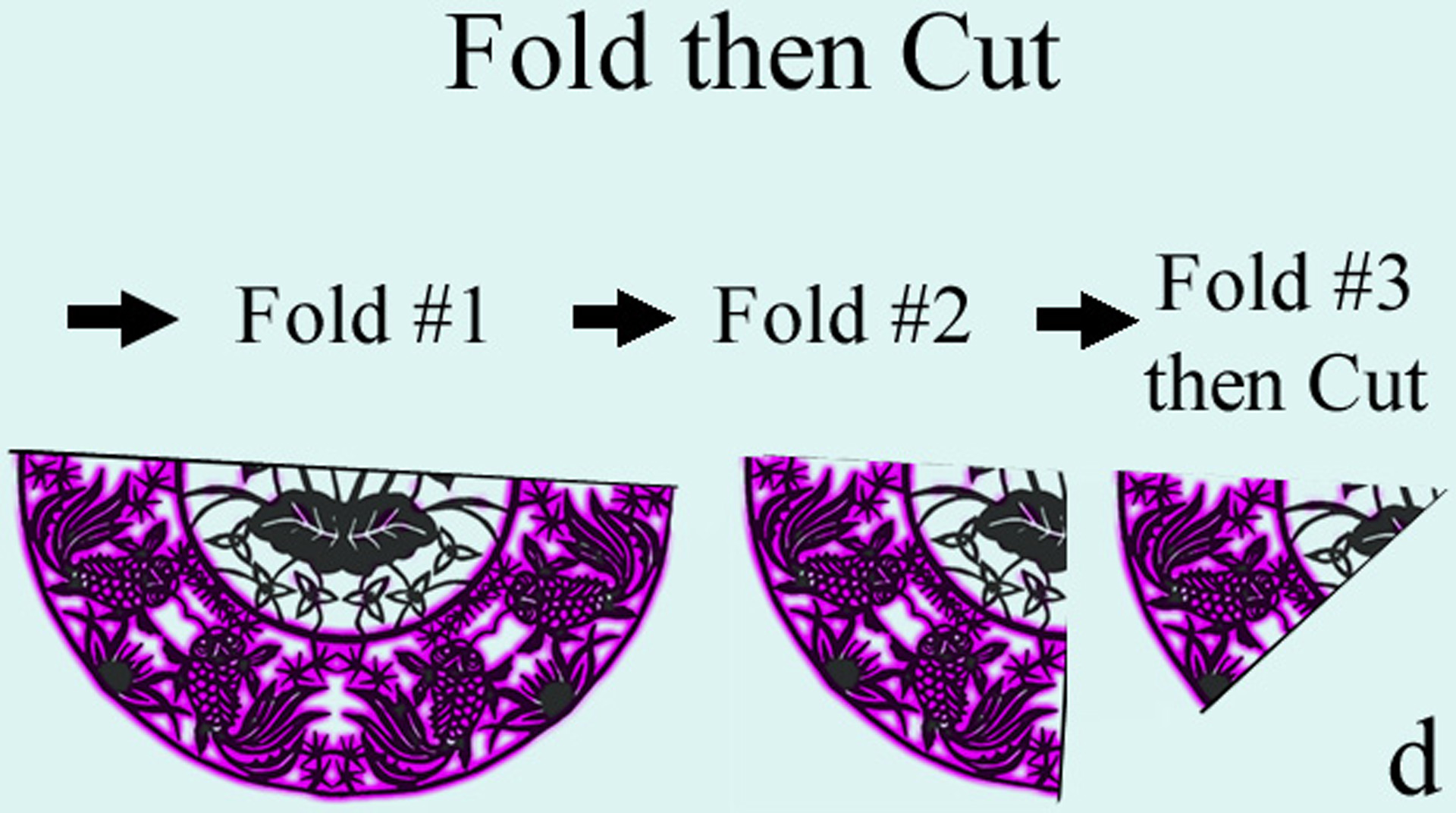
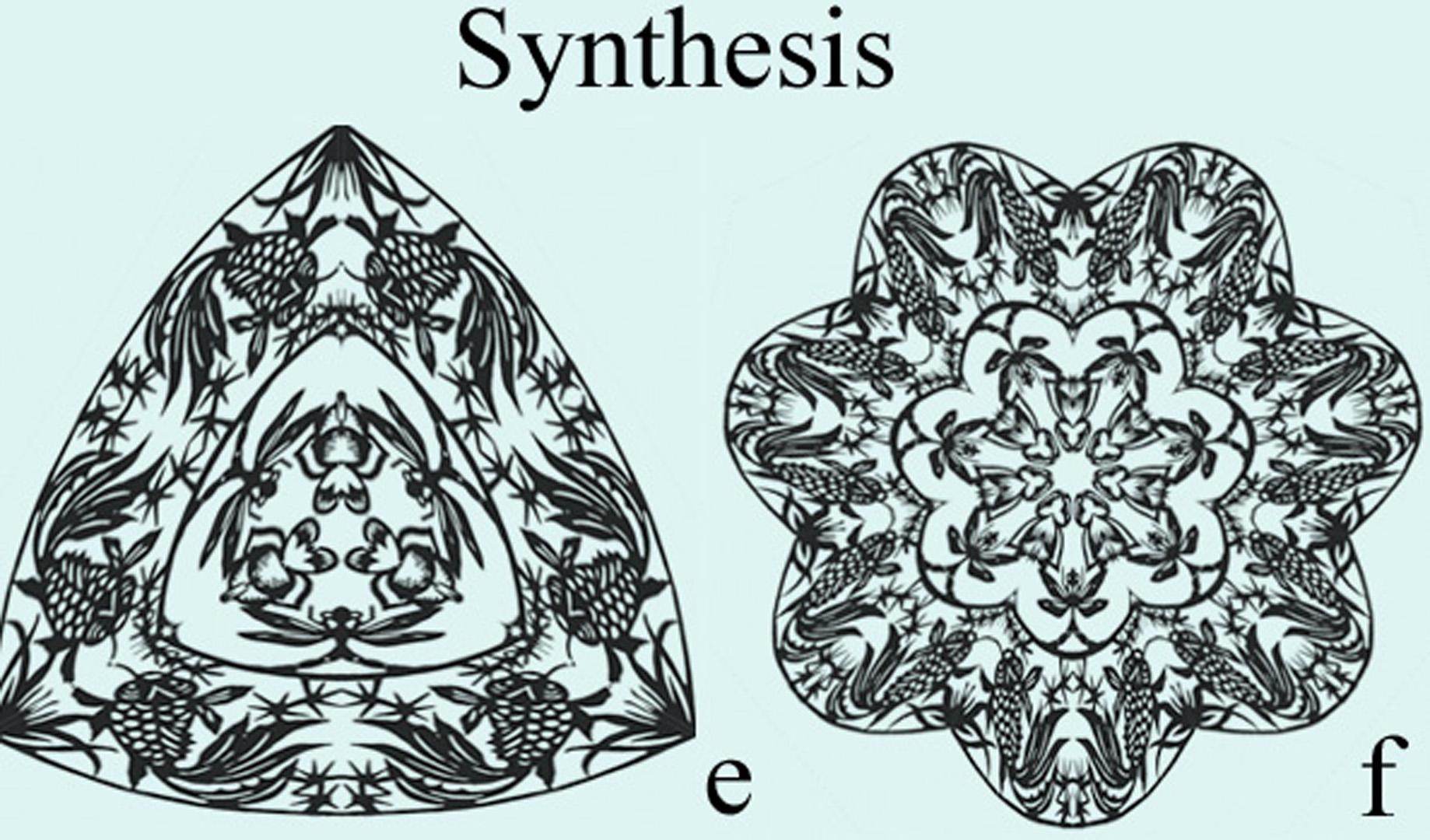
Symmetry or deviation from symmetry is the central theme of many different art forms, ranging from music, painting, sculpture to various decorative and folk arts. One of the most popular and accessible such art forms is that of papercutting, where symmetry is used both in its artistic design and its geneation process. Intrigued by this effective, seamless combination, we are interested in using computational means to reveal the relationship between the form and generative process for a digitized papercut-pattern. Regardless of how complicated and diverse a papercutting design might be, each papercut pattern is connected and often presents global or local symmetry. We are interested in those papercut-patterns containing non-trivial global and/or local reflection symmetry such that fold-then-cut operations are necessary steps in their generative process. The computational challenges in symmetry-based analysis of real-world patterns include discriminating different types of symmetry structures in global and local regions; and distinguishing between “near-symmetries” as deviations from implied symmetry and truly asymmetric designs. [Demaine and Lubiw 2000] show that any polygonal shapes can be generated through multiple foldings followed by a single straight- cut. The simultaneous foldings required, however, are often rather challenging physically. Formal and algorithmic treatment of general papercut patterns with a non-polyhedral nature remains scarce.

Demaine, E. D., D. M., And Lubiw, A. 2000. Folding and cutting paper. In JCDCG ’98: Revised Papers from the Japanese Conference on Discrete and Computational Geometry, Springer-Verlag, 104–118.