“Affine interpolation in a lie group framework” by Bansal and Tatu
Conference:
Type(s):
Title:
- Affine interpolation in a lie group framework
Session/Category Title: Deformation and FEM
Presenter(s)/Author(s):
Abstract:
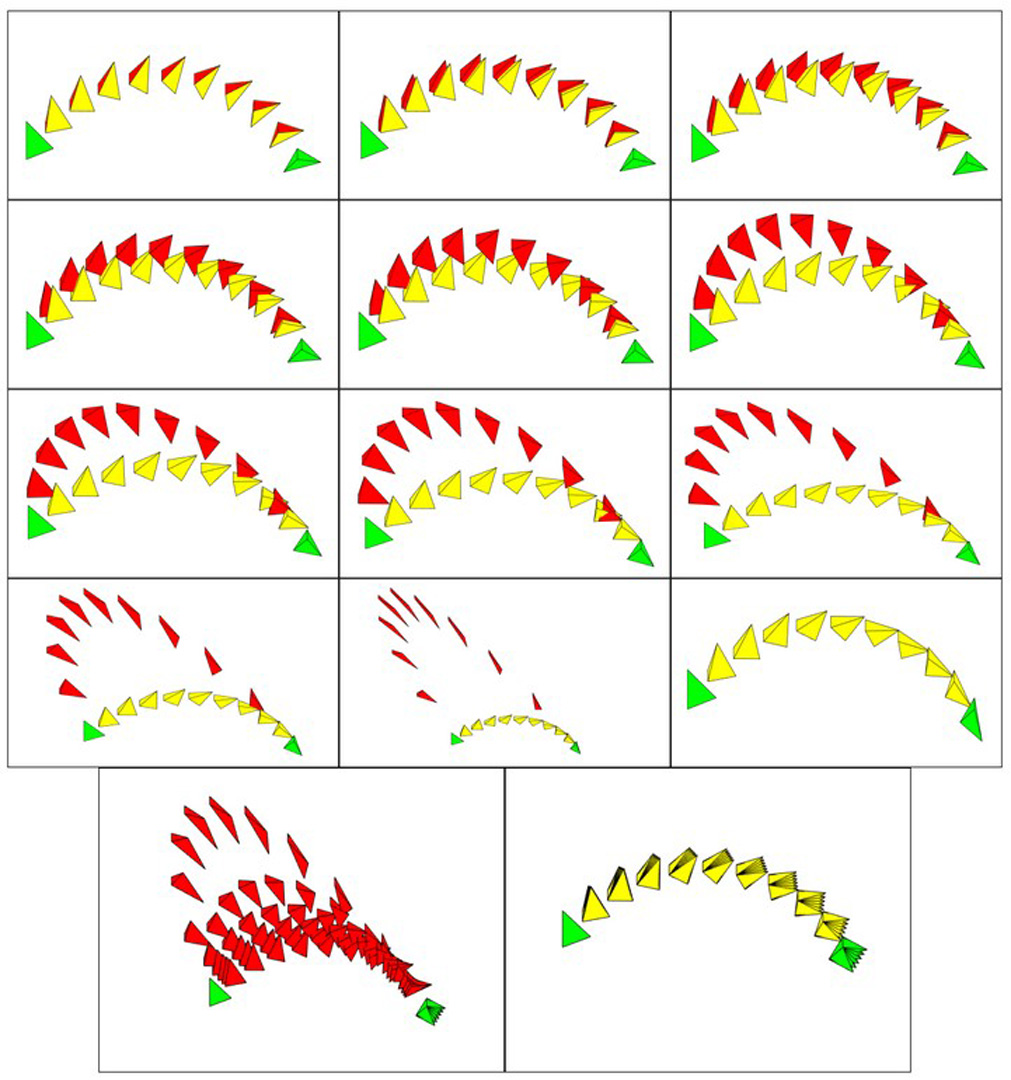
Affine transformations are of vital importance in many tasks pertaining to motion design and animation. Interpolation of affine transformations is non-trivial. Typically, the given affine transformation is decomposed into simpler components which are easier to interpolate. This may lead to unintuitive results, while in some cases, such solutions may not work. In this work, we propose an interpolation framework which is based on a Lie group representation of the affine transformation. The Lie group representation decomposes the given transformation into simpler and meaningful components, on which computational tools like the exponential and logarithm maps are available in closed form. Interpolation exists for all affine transformations while preserving a few characteristics of the original transformation. A detailed analysis and several experiments of the proposed framework are included.
References:
1. Marc Alexa. 2002. Linear combination of transformations. In ACM Transactions on Graphics (TOG), Vol. 21. ACM, 380–387. Google ScholarDigital Library
2. Marc Alexa, Daniel Cohen-Or, and David Levin. 2000. As-rigid-as-possible shape interpolation. In Proceedings of the 27th annual conference on Computer graphics and interactive techniques. ACM Press/Addison-Wesley Publishing Co., 157–164. Google ScholarDigital Library
3. Kevin G Der, Robert W Sumner, and Jovan Popović. 2006. Inverse kinematics for reduced deformable models. In ACM Transactions on Graphics (TOG), Vol. 25. ACM, 1174–1179. Google ScholarDigital Library
4. Oren Freifeld and Michael J. Black. 2012. Lie Bodies: A Manifold Representation of 3D Human Shape. In European Conf. on Computer Vision (ECCV) (Part I, LNCS 7572). Springer-Verlag, 1–14. Google ScholarDigital Library
5. Jean Gallier and Jocelyn Quaintance. 2017. Notes on Differential Geometry and Lie Groups. (2017). Available online at www.cis.upenn.edu/jean/gbooks/manif.html.Google Scholar
6. Alec Jacobson, Zhigang Deng, Ladislav Kavan, and JP Lewis. 2014. Skinning: Real-time Shape Deformation. In ACM SIGGRAPH 2014 Courses. Google ScholarDigital Library
7. S. Kaji, S. Hirose, S. Sakata, Y. Mizoguchi, and K. Anjyo. 2012. Mathematical Analysis on Affine Maps for 2D Shape Interpolation. In Proceedings of the ACM SIGGRAPH/Eurographics Symposium on Computer Animation (SCA ’12). Eurographics Association, Goslar Germany, Germany, 71–76. http://dl.acm.org/citation.cfm?id=2422356.2422368 Google ScholarDigital Library
8. Ladislav Kavan, Steven Collins, Jiří Žára, and Carol O’Sullivan. 2008. Geometric skinning with approximate dual quaternion blending. ACM Transactions on Graphics (TOG) 27, 4 (2008), 105. Google ScholarDigital Library
9. Ladislav Kavan and Jiří Žára. 2005. Spherical blend skinning: a real-time deformation of articulated models. In Proceedings of the 2005 symposium on Interactive 3D graphics and games. ACM, 9–16. Google ScholarDigital Library
10. Jun Li and Peng-wei Hao. 2006. Smooth interpolation on homogeneous matrix groups for computer animation. Journal of Zhejiang University-SCIENCE A 7, 7 (2006), 1168–1177.Google ScholarCross Ref
11. Nadia Magnenat-Thalmann, Richard Laperrire, and Daniel Thalmann. 1988. Joint-dependent local deformations for hand animation and object grasping. In Proceedings on Graphics interface. Google ScholarDigital Library
12. Richard M. Murray, S. Shankar Sastry, and Li Zexiang. 1994. A Mathematical Introduction to Robotic Manipulation (1st ed.). CRC Press, Inc., Boca Raton, FL, USA. Google ScholarDigital Library
13. Hiroyuki Ochiai and Ken Anjyo. 2013. Mathematical description of motion and deformation: from basics to graphics applications. In SIGGRAPH Asia 2013, Hong Kong, China, November 19–22, 2013, Courses. 2:1–2:47. Google ScholarDigital Library
14. M. M. Postnikov. 2001. Geometry VI: Riemannian Geometry. Springer-Verlag Berlin Heidelberg.Google ScholarCross Ref
15. Jarek Rossignac and Álvar Vinacua. 2011. Steady affine motions and morphs. ACM Transactions on Graphics (TOG) 30, 5 (2011), 116. Google ScholarDigital Library
16. J. M. Selig. 2010. Geometric Fundamentals of Robotics (2nd ed.). Springer Publishing Company, Incorporated. Google ScholarDigital Library
17. Ken Shoemake. 1985. Animating Rotation with Quaternion Curves. SIGGRAPH Comput. Graph. 19, 3 (July 1985), 245–254. Google ScholarDigital Library
18. Ken. Shoemake. 1992. Matrix animation and polar decomposition. Graphics Interface’92, 1992 (1992). Google ScholarDigital Library
19. Robert W. Sumner, Matthias Zwicker, Craig Gotsman, and Jovan Popović. 2005. Mesh-based Inverse Kinematics. ACM Trans. Graph. 24, 3 (July 2005), 488–495. Google ScholarDigital Library
20. B. Whited, G. Noris, M. Simmons, R. Sumner, M. Gross, and J. Rossignac. 2010. BetweenIT: An Interactive Tool for Tight Inbetweening. Comput. Graphics Forum (Proc. Eurographics) 29, 2 (2010), 605–614.Google ScholarCross Ref
21. Milos Zefran and Vijay Kumar. 1998. Interpolation schemes for rigid body motions. Computer-Aided Design 30, 3 (1998), 179 — 189. Motion Design and Kinematics.Google ScholarCross Ref