“Two-layer sparse compression of dense-weight blend skinning” by Le and Deng
Conference:
Type(s):
Title:
- Two-layer sparse compression of dense-weight blend skinning
Session/Category Title: Skinning & Deformation
Presenter(s)/Author(s):
Moderator(s):
Abstract:
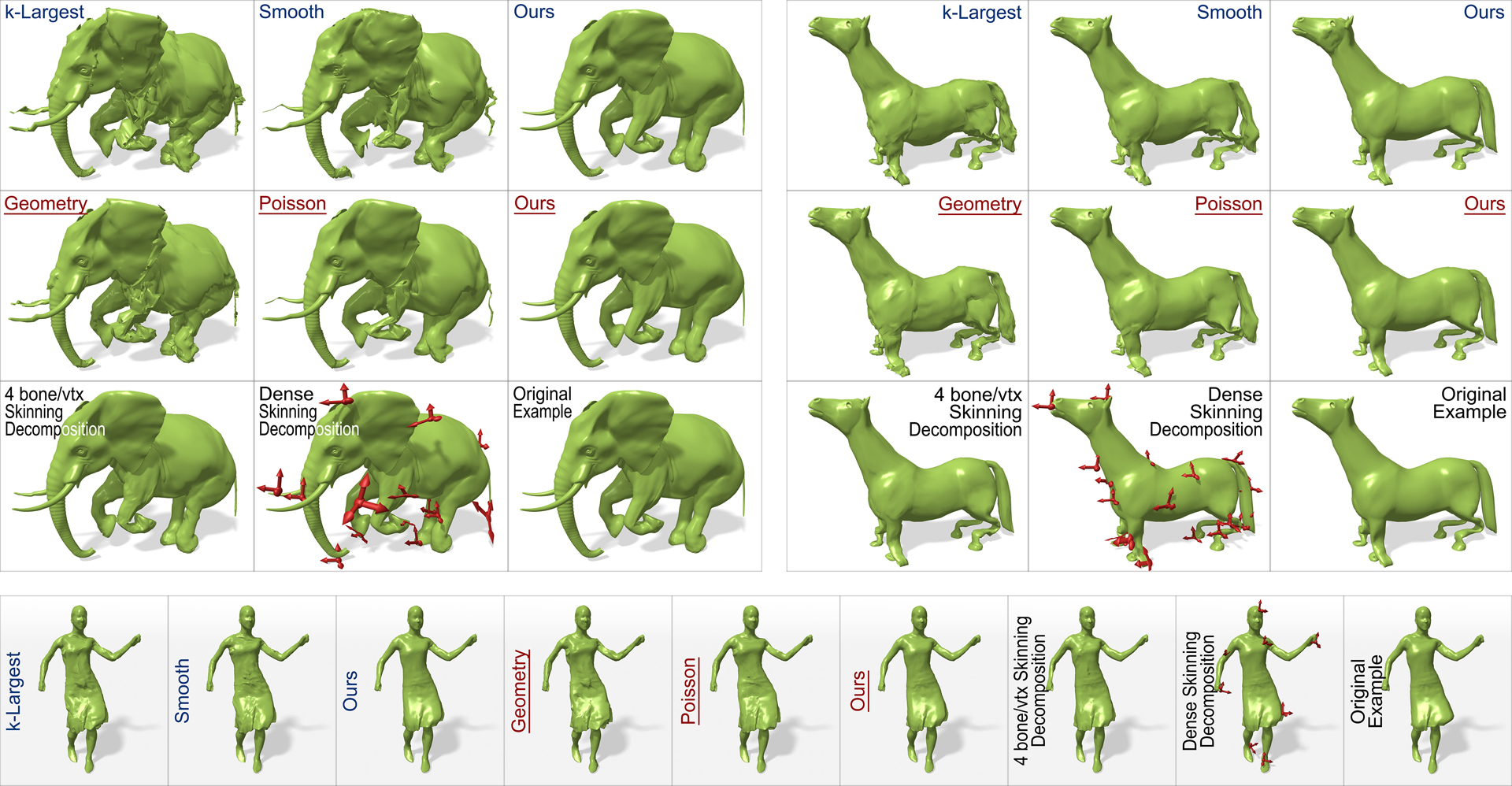
Weighted linear interpolation has been widely used in many skinning techniques including linear blend skinning, dual quaternion blend skinning, and cage based deformation. To speed up performance, these skinning models typically employ a sparseness constraint, in which each 3D model vertex has a small fixed number of non-zero weights. However, the sparseness constraint also imposes certain limitations to skinning models and their various applications. This paper introduces an efficient two-layer sparse compression technique to substantially reduce the computational cost of a dense-weight skinning model, with insignificant loss of its visual quality. It can directly work on dense skinning weights or use example-based skinning decomposition to further improve its accuracy. Experiments and comparisons demonstrate that the introduced sparse compression model can significantly outperform state of the art weight reduction algorithms, as well as skinning decomposition algorithms with a sparseness constraint.
References:
1. Aharon, M., Elad, M., and Bruckstein, A. 2006. K-SVD: An Algorithm for Designing Overcomplete Dictionaries for Sparse Representation. IEEE Transactions on Signal Processing 54, 11 (Nov.), 4311–4322. Google ScholarDigital Library
2. Baran, I., and Popović, J. 2007. Automatic rigging and animation of 3d characters. ACM Trans. Graph. 26 (July). Google ScholarDigital Library
3. Borosán, P., Jin, M., DeCarlo, D., Gingold, Y., and Nealen, A. 2012. Rigmesh: automatic rigging for part-based shape modeling and deformation. ACM Trans. Graph. 31, 6 (Nov.), 198:1–198:9. Google ScholarDigital Library
4. Hasler, N., Thormählen, T., Rosenhahn, B., and Seidel, H.-P. 2010. Learning skeletons for shape and pose. In I3D’10, 23–30. Google ScholarDigital Library
5. Jacobson, A., and Sorkine, O. 2011. Stretchable and twistable bones for skeletal shape deformation. ACM Trans. Graph. 30 (Dec.), 165:1–165:8. Google ScholarDigital Library
6. Jacobson, A., Baran, I., Popović, J., and Sorkine, O. 2011. Bounded biharmonic weights for real-time deformation. ACM Trans. Graph. 30, 4 (July), 78:1–78:8. Google ScholarDigital Library
7. Jacobson, A., Baran, I., Kavan, L., Popović, J., and Sorkine, O. 2012. Fast automatic skinning transformations. ACM Trans. Graph. 31, 4 (July), 77:1–77:10. Google ScholarDigital Library
8. Jacobson, A., Weinkauf, T., and Sorkine, O. 2012. Smooth shape-aware functions with controlled extrema. Comp. Graph. Forum 31, 5 (Aug.), 1577–1586. Google ScholarDigital Library
9. James, D. L., and Twigg, C. D. 2005. Skinning mesh animations. ACM Trans. Graph. 24 (July), 399–407. Google ScholarDigital Library
10. Joshi, P., Meyer, M., DeRose, T., Green, B., and Sanocki, T. 2007. Harmonic coordinates for character articulation. ACM Trans. Graph. 26, 3 (July). Google ScholarDigital Library
11. Ju, T., Schaefer, S., and Warren, J. 2005. Mean value coordinates for closed triangular meshes. ACM Trans. Graph. 24, 3 (July), 561–566. Google ScholarDigital Library
12. Kavan, L., and Sorkine, O. 2012. Elasticity-inspired deformers for character articulation. ACM Trans. Graph. 31, 6 (Nov.), 196:1–196:8. Google ScholarDigital Library
13. Kavan, L., McDonnell, R., Dobbyn, S., Žára, J., and O’Sullivan, C. 2007. Skinning arbitrary deformations. In I3D’07, 53–60. Google ScholarDigital Library
14. Kavan, L., Collins, S., Žára, J., and O’Sullivan, C. 2008. Geometric skinning with approximate dual quaternion blending. ACM Trans. Graph. 27 (November), 105:1–105:23. Google ScholarDigital Library
15. Kavan, L., Collins, S., and O’Sullivan, C. 2009. Automatic linearization of nonlinear skinning. In I3D’09, 49–56. Google ScholarDigital Library
16. Kavan, L., Sloan, P.-P., and O’Sullivan, C. 2010. Fast and efficient skinning of animated meshes. Comput. Graph. Forum 29, 2, 327–336.Google ScholarCross Ref
17. Kry, P. G., James, D. L., and Pai, D. K. 2002. Eigenskin: real time large deformation character skinning in hardware. In SCA’02, 153–159. Google ScholarDigital Library
18. Landreneau, E., and Schaefer, S. 2010. Poisson-based weight reduction of animated meshes. Comput. Graph. Forum 29, 6, 1945–1954.Google ScholarCross Ref
19. Le, B. H., and Deng, Z. 2012. Smooth skinning decomposition with rigid bones. ACM Trans. Graph. 31, 6 (Nov.), 199:1–199:10. Google ScholarDigital Library
20. Lee, H., Battle, A., Raina, R., and Ng, A. Y. 2007. Efficient sparse coding algorithms. In Advances in Neural Information Processing Systems 19. MIT Press, 801–808.Google Scholar
21. Lewis, J. P., Cordner, M., and Fong, N. 2000. Pose space deformation: a unified approach to shape interpolation and skeleton-driven deformation. In Proc. of ACM SIGGRAPH’00, 165–172. Google ScholarDigital Library
22. Mairal, J., Bach, F., Ponce, J., and Sapiro, G. 2010. Online learning for matrix factorization and sparse coding. J. Mach. Learn. Res. 11 (Mar.), 19–60. Google ScholarDigital Library
23. Mallat, S., and Zhang, Z. 1993. Matching pursuits with time-frequency dictionaries. Trans. Sig. Proc. 41, 12 (Dec.), 3397–3415. Google ScholarDigital Library
24. Marquardt, D. W. 1963. An Algorithm for Least-Squares Estimation of Nonlinear Parameters. SIAM Journal on Applied Mathematics 11, 2, 431–441.Google ScholarCross Ref
25. Merry, B., Marais, P., and Gain, J. 2006. Animation space: A truly linear framework for character animation. ACM Trans. Graph. 25 (October), 1400–1423. Google ScholarDigital Library
26. Mohr, A., and Gleicher, M. 2003. Building efficient, accurate character skins from examples. ACM Trans. Graph. 22 (July), 562–568. Google ScholarDigital Library
27. Nguyen, H. 2007. GPU gems 3 (first edition), chapter 4.4. Addison-Wesley Professional. Google ScholarDigital Library
28. Nocedal, J., and Wright, S. 2000. Numerical Optimization. Springer.Google Scholar
29. Schaefer, S., and Yuksel, C. 2007. Example-based skeleton extraction. In SGP’07, 153–162. Google ScholarDigital Library
30. Sederberg, T. W., and Parry, S. R. 1986. Free-form deformation of solid geometric models. SIGGRAPH Comput. Graph. 20, 4 (Aug.), 151–160. Google ScholarDigital Library
31. Sumner, R. W., and Popović, J. 2004. Deformation transfer for triangle meshes. ACM Trans. Graph. 23 (August), 399–405. Google ScholarDigital Library
32. Vlasic, D., Baran, I., Matusik, W., and Popović, J. 2008. Articulated mesh animation from multi-view silhouettes. ACM Trans. Graph. 27 (August), 97:1–97:9. Google ScholarDigital Library
33. Wang, X. C., and Phillips, C. 2002. Multi-weight enveloping: least-squares approximation techniques for skin animation. In SCA’02, 129–138. Google ScholarDigital Library
34. Warren, J., Schaefer, S., Hirani, A. N., and Desbrun, M. 2004. Barycentric coordinates for convex sets. Tech. rep., Advances in Computational and Applied Mathematics.Google Scholar
35. Zou, H., and Hastie, T. 2005. Regularization and variable selection via the elastic net. Journal of the Royal Statistical Society, Series B 67, 301–320.Google ScholarCross Ref