“Topology-constrained surface reconstruction from cross-sections” by Zou, Holloway, Carr and Ju

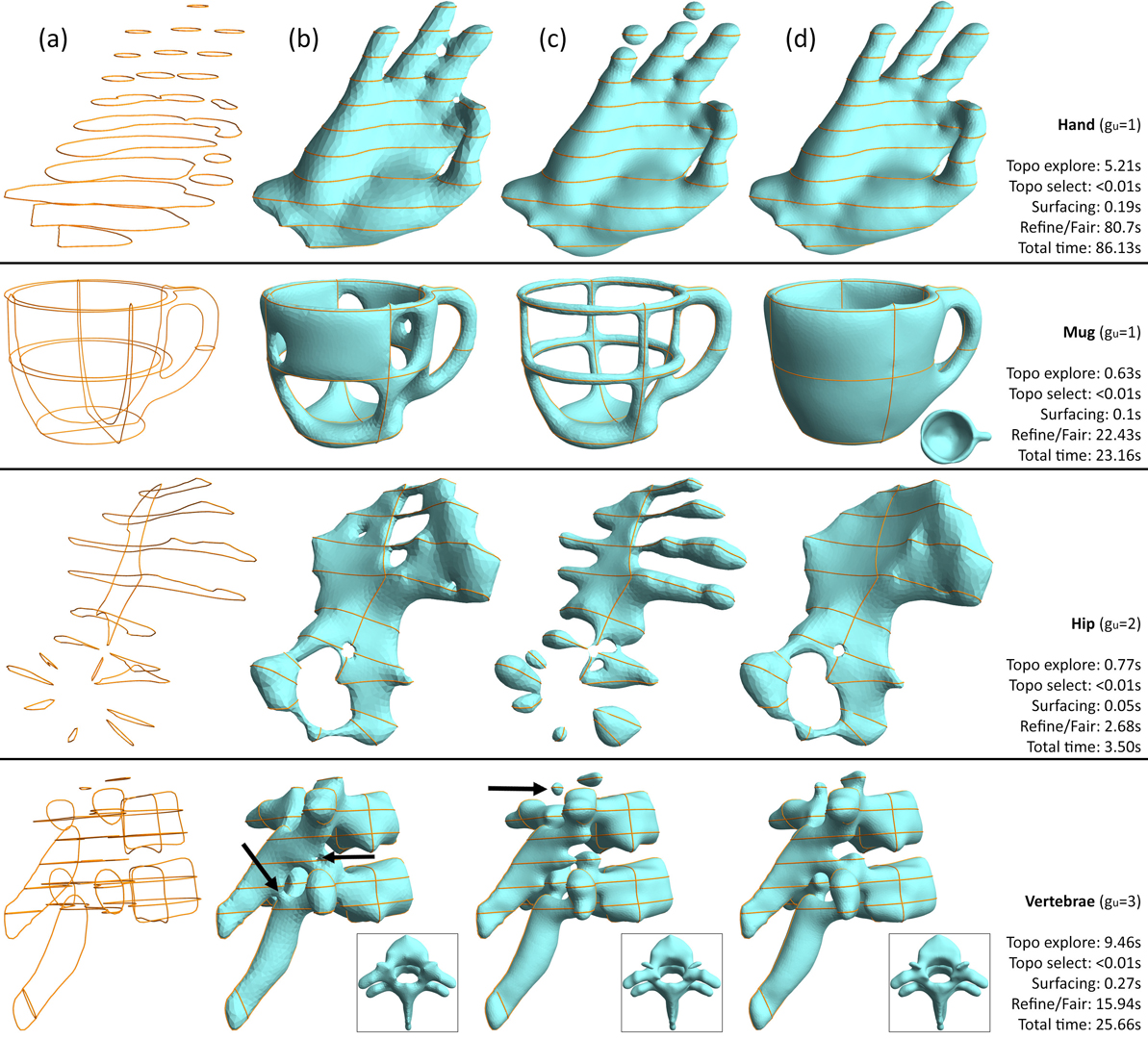
In this work we detail the first algorithm that provides topological control during surface reconstruction from an input set of planar cross-sections. Our work has broad application in a number of fields including surface modeling and biomedical image analysis, where surfaces of known topology must be recovered. Given curves on arbitrarily oriented cross-sections, our method produces a manifold interpolating surface that exactly matches a user-specified genus. The key insight behind our approach is to formulate the topological search as a divide-and-conquer optimization process which scores local sets of topologies and combines them to satisfy the global topology constraint. We further extend our method to allow image data to guide the topological search, achieving even better results than relying on the curves alone. By simultaneously satisfying both geometric and topological constraints, we are able to produce accurate reconstructions with fewer input cross-sections, hence reducing the manual time needed to extract the desired shape.

1. Amini, O., Boissonnat, J., and Memari, P. 2013. Geometric tomography with topological guarantees. Discrete & Computational Geometry 50, 4, 821–856.Google ScholarDigital Library
2. Attene, M., Campen, M., and Kobbelt, L. 2013. Polygon mesh repairing: An application perspective. ACM Comput. Surv. 45, 2 (Mar.), 15:1–15:33. Google ScholarDigital Library
3. Bajaj, C. L., Coyle, E. J., and Lin, K.-N. 1996. Arbitrary topology shape reconstruction from planar cross sections. Graph. Models Image Process. 58, 6, 524–543. Google ScholarDigital Library
4. Barequet, G., and Sharir, M. 1996. Piecewise-linear interpolation between polygonal slices. Computer Vision and Image Understanding 63, 251–272. Google ScholarDigital Library
5. Barequet, G., and Vaxman, A. 2007. Nonlinear interpolation between slices. In SPM ’07: Proceedings of the 2007 ACM symposium on Solid and physical modeling, 97–107. Google ScholarDigital Library
6. Barequet, G., and Vaxman, A. 2009. Reconstruction of multi-label domains from partial planar cross-sections. Comput. Graph. Forum 28, 5, 1327–1337.Google ScholarDigital Library
7. Barequet, G., Goodrich, M. T., Levi-Steiner, A., and Steiner, D. 2004. Straight-skeleton based contour interpolation. Graph. Models 65, 323–350.Google Scholar
8. Barequet, G., Gotsman, C., and Sidlesky, A. 2006. Polygon reconstruction from line cross-sections. In Proceedings of the 18th Annual Canadian Conference on Computational Geometry, CCCG 2006, August 14–16, 2006, Queen’s University, Ontario, Canada.Google Scholar
9. Bazin, P., and Pham, D. L. 2007. Topology-preserving tissue classification of magnetic resonance brain images. IEEE Trans. Med. Imaging 26, 4, 487–496.Google ScholarCross Ref
10. Bermano, A., Vaxman, A., and Gotsman, C. 2011. Online reconstruction of 3d objects from arbitrary cross-sections. ACM Trans. Graph. 30, 5 (Oct.), 113:1–113:11. Google ScholarDigital Library
11. Boissonnat, J.-D., and Memari, P. 2007. Shape reconstruction from unorganized cross-sections. In SGP ’07: Proceedings of the fifth Eurographics symposium on Geometry processing, 89–98. Google ScholarDigital Library
12. Boissonnat, J.-D. 1988. Shape reconstruction from planar cross sections. Comput. Vision Graph. Image Process. 44, 1, 1–29. Google ScholarDigital Library
13. Cheng, S.-W., and Dey, T. K. 1999. Improved constructions of delaunay based contour surfaces. In SMA ’99: Proceedings of the fifth ACM symposium on Solid modeling and applications, ACM Press, 322–323. Google ScholarDigital Library
14. Fuchs, H., Kedem, Z. M., and Uselton, S. P. 1977. Optimal surface reconstruction from planar contours. Commun. ACM 20, 10, 693–702. Google ScholarDigital Library
15. Grady, L. 2006. Random walks for image segmentation. IEEE Trans. Pattern Anal. Mach. Intell. 28, 11 (Nov.), 1768–1783. Google ScholarDigital Library
16. Herman, G. T., Zheng, J., and Bucholtz, C. A. 1992. Shape-based interpolation. IEEE Comput. Graph. Appl. 12, 3, 69–79. Google ScholarDigital Library
17. Ijiri, T., Yoshizawa, S., Yokota, H., and Igarashi, T. 2014. Flower Modeling via X-ray Computed Tomography. ACM Trans. Graph. 33, 4, to appear. Proc. of SIGGRAPH’14. Google ScholarDigital Library
18. Ju, T., Warren, J. D., Carson, J., Eichele, G., Thaller, C., Chiu, W., Bello, M., and Kakadiaris, I. A. 2005. Building 3d surface networks from 2d curve networks with application to anatomical modeling. The Visual Computer 21, 8-10, 764–773.Google ScholarCross Ref
19. Ju, T., Zhou, Q.-Y., and Hu, S.-M. 2007. Editing the topology of 3d models by sketching. ACM Trans. Graph. 26, 3 (July). Google ScholarDigital Library
20. Keppel, E. 1975. Approximating complex surfaces by triangulation of contour lines. IBM Journal of Research and Development 19, 1, 2–11. Google ScholarDigital Library
21. Knuth, D. E. 2000. Dancing links. Millenial Perspectives in Computer Science (Nov), 187–214.Google Scholar
22. Liepa, P. 2003. Filling holes in meshes. In Proceedings of the 2003 Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, SGP ’03, 200–205. Google ScholarDigital Library
23. Liu, L., Bajaj, C., Deasy, J., Low, D. A., and Ju, T. 2008. Surface reconstruction from non-parallel curve networks. Comput. Graph. Forum 27, 2, 155–163.Google ScholarCross Ref
24. Meyers, D., Skinner, S., and Sloan, K. 1992. Surfaces from contours. ACM Trans. Graph. 11, 3, 228–258. Google ScholarDigital Library
25. Oliva, J.-M., Perrin, M., and Coquillart, S. 1996. 3d reconstruction of complex polyhedral shapes from contours using a simplified generalized voronoi diagram. Computer Graphics Forum 15, 3, 397–408.Google ScholarCross Ref
26. Sharf, A., Lewiner, T., Shklarski, G., Toledo, S., and Cohen-Or, D. 2007. Interactive topology-aware surface reconstruction. ACM Trans. Graph. 26, 3 (July). Google ScholarDigital Library
27. Si, H., 2007. TetGen. a quality tetrahedral mesh generator and three-dimensional delaunay triangulator.Google Scholar
28. Turk, G., and O’Brien, J. F. 1999. Shape transformation using variational implicit functions. In SIGGRAPH ’99: Proceedings of the 26th annual conference on Computer graphics and interactive techniques, ACM Press/Addison-Wesley Publishing Co., 335–342. Google ScholarDigital Library
29. Van Kreveld, M., Van Oostrum, R., Bajaj, C., Pascucci, V., and Schikore, D. 1997. Contour trees and small seed sets for isosurface traversal. In Proceedings of the Thirteenth Annual Symposium on Computational Geometry, SCG ’97, 212–220. Google ScholarDigital Library
30. Wood, Z. J., Hoppe, H., Desbrun, M., and Schröder, P. 2004. Removing excess topology from isosurfaces. ACM Trans. Graph. 23, 2, 190–208. Google ScholarDigital Library
31. Xu, G., Pan, Q., and Bajaj, C. 2006. Discrete surface modelling using partial differential equations. Computer Aided Geometric Design 23, 2, 125–145. Google ScholarDigital Library
32. Yin, K., Huang, H., Zhang, H., Gong, M., Cohen-Or, D., and Chen, B. 2014. Morfit: Interactive surface reconstruction from incomplete point clouds with curve-driven topology and geometry control. ACM Trans. Graph. 33, 6 (Nov.), 202:1–202:12. Google ScholarDigital Library
33. Zeng, Y., Samaras, D., Chen, W., and Peng, Q. 2008. Topology cuts: A novel min-cut/max-flow algorithm for topology preserving segmentation in N-D images. Computer Vision and Image Understanding 112, 1, 81–90. Google ScholarDigital Library
34. Zhou, Q.-Y., Ju, T., and Hu, S.-M. 2007. Topology repair of solid models using skeletons. IEEE Transactions on Visualization and Computer Graphics 13, 4 (July), 675–685. Google ScholarDigital Library
35. Zhou, S., Jiang, C., and Lefebvre, S. 2014. Topologyconstrained synthesis of vector patterns. ACM Transactions on Graphics (Proc. SIGGRAPH Aisa) 33. Google ScholarDigital Library