“Stratified sampling of spherical triangles” by Arvo
Conference:
Type(s):
Title:
- Stratified sampling of spherical triangles
Presenter(s)/Author(s):
Abstract:
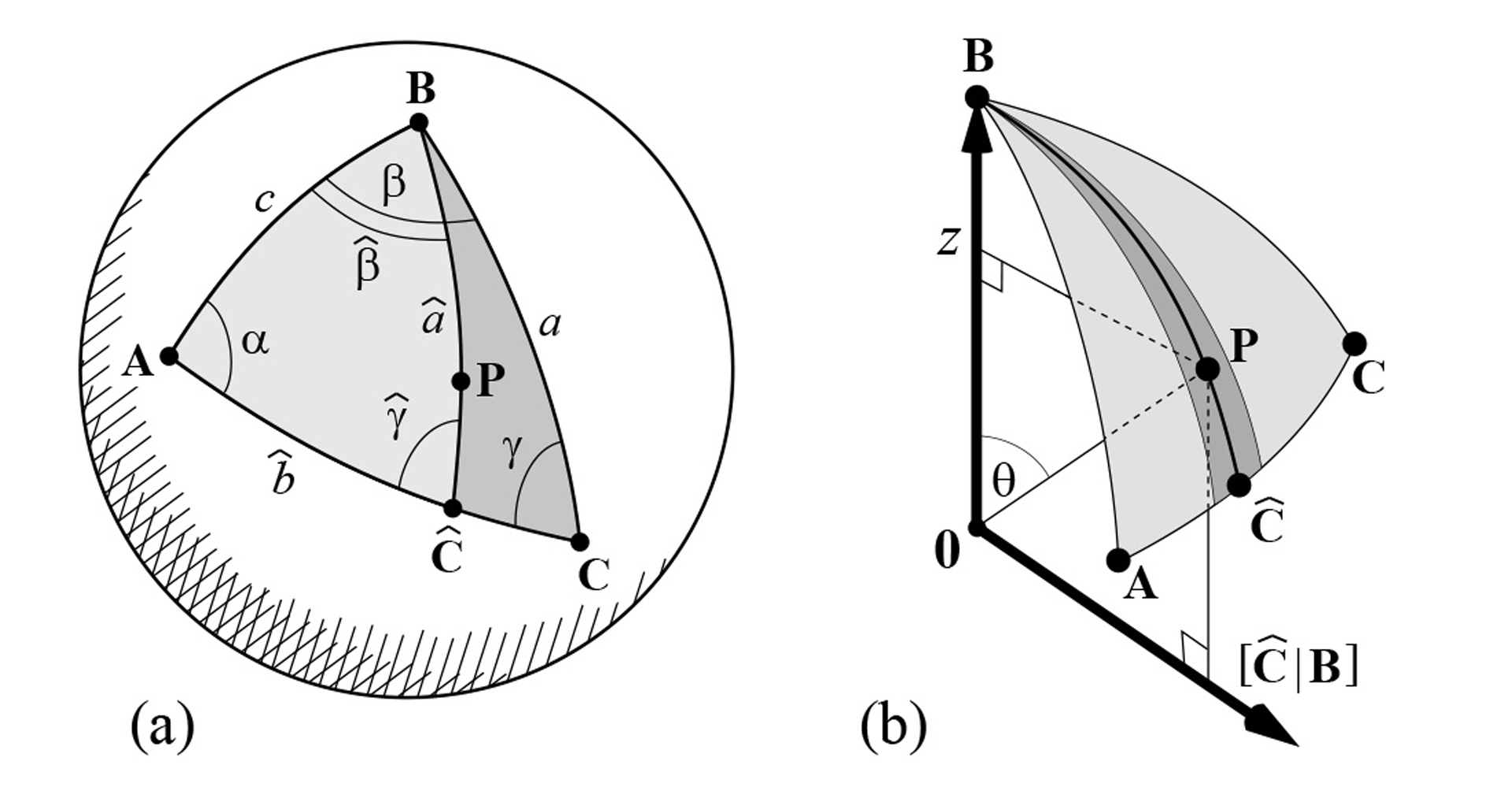
We present an algorithm for generating uniformly distributed random samples from arbitrary spherical triangles. The algorithm is based on a transformation of the unit square and easily accommodates stratified sampling, an effective means of reducing variance. With the new algorithm it is straightforward to perform stratified sampling of the solid angle subtended by an arbitrary polygon; this is a fundamental operation in image synthesis which has not been addressed in the Monte Carlo literature. We derive the required transformation using elementary spherical trigonometry and provide the complete sampling algorithm.
References:
1. BERGER, M. Geometry, Volume II. Springer-Verlag, New York, 1987. Translated by M. Cole and S. Levy.
2. CooK, R. L. Stochastic sampling in computer graphics. ACM Transactions on Graphics 5, 1 (1986), 51-72.
3. HANRAHAN, P., SALZMAN, D., AND AUPPERLE, L. A rapid hierarchical radiosity algorithm. Computer Graphics 25, 4 (July 1991), 197-206.
4. RUBINSTEIN, R.Y. Simulation and the Monte Carlo Method. John Wiley ~z Sons, New York, 1981.
5. SHIRLEY, P., WANG, C., AND ZIMMERMAN, K. Monte carlo methods for direct lighting calculations. A CM Transactions on Graphics (1995). To appear.
6. SPANIER, J., AND GELBARD, E. M. Monte Carlo Principles and Neutron Transport Problems. Addison-Wesley, Reading, Massachusetts, 1969.
7. TURK, G. Generating random points in triangles. In Graphics Gems, A. S. Glassner, Ed. Academic Press, New York, 1990, pp. 24-28.