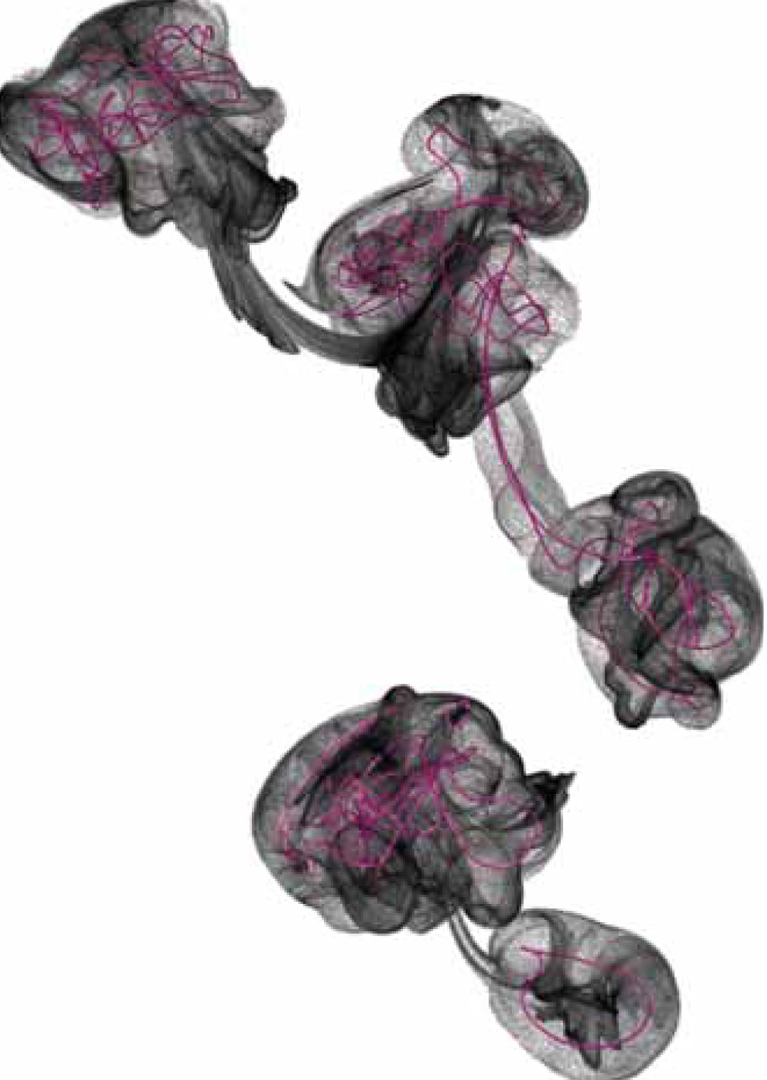
“Smoke rings from smoke” by Weißmann, Pinkall and Schröder
Conference:
Type(s):
Title:
- Smoke rings from smoke
Session/Category Title: Fluids
Presenter(s)/Author(s):
Moderator(s):
Abstract:
We give an algorithm which extracts vortex filaments (“smoke rings”) from a given 3D velocity field. Given a filament strength h > 0, an optimal number of vortex filaments, together with their extent and placement, is given by the zero set of a complex valued function over the domain. This function is the global minimizer of a quadratic energy based on a Schrödinger operator. Computationally this amounts to finding the eigenvector belonging to the smallest eigenvalue of a Laplacian type sparse matrix.Turning traditional vector field representations of flows, for example, on a regular grid, into a corresponding set of vortex filaments is useful for visualization, analysis of measured flows, hybrid simulation methods, and sparse representations. To demonstrate our method we give examples from each of these.
References:
1. Angelidis, A., and Neyret, F. 2005. Simulation of Smoke based on Vortex Filament Primitives. In Proc. Symp. Comp. Anim., 87–96. Google ScholarDigital Library
2. Bernard, P. S. 2006. Turbulent Flow Properties of Large-scale Vortex Systems. PNAS 103, 27, 10174–10179.Google ScholarCross Ref
3. Bernard, P. S. 2009. Vortex Filament Simulation of the Turbulent Coflowing Jet. Phys. Fluids 21, 2.Google Scholar
4. Brochu, T., Keeler T., and Bridson, R. 2012. Linear-Time Smoke Animation with Vortex Sheet Meshes. In Proc. Symp. Comp. Anim., 87–95. Google ScholarDigital Library
5. Chatelain, P., Curioni, A., Bergdorf, M., Rossinelli, D., Andreoni, W., and Koumoutsakos, P. 2008. Billion Vortex Particle Direct Numerical Simulations of Aircraft Wakes. Comp. Meth. Appl. Mech. & Eng. 197, 13–16, 1296–1304.Google ScholarCross Ref
6. Chorin, A. J. 1990. Hairpin Removal in Vortex Interactions. J. Comput. Phys. 91, 1, 1–21. Google ScholarDigital Library
7. Chorin, A. J. 1993. Hairpin Removal in Vortex Interactions II. J. Comput. Phys. 107, 1, 1–9. Google ScholarDigital Library
8. Christiansen, S. H., and Halvorsen, T. G. 2011. A Gauge Invariant Discretization on Simplicial Grids of the Schrödinger Eigenvalue Problem in an Electromagnetic Field. SIAM J. Numer. Anal. 49, 1, 331–345. Google ScholarDigital Library
9. Crane, K., de Goes, F., Desbrun, M., and Schröder, P. 2013. Digital Geometry Processing with Discrete Exterior Calculus. In ACM SIGGRAPH 2013 Courses, 7:1–7:126. Google ScholarDigital Library
10. Desbrun, M., Kanso, E., and Tong, Y. 2008. Discrete Differential Forms for Computational Modeling. In Discrete Differential Geometry, A. I. Bobenko, P. Schröder, J. M. Sullivan, and G. M. Ziegler, Eds., Vol. 38 of Oberwolfach Seminars. Birkhäuser Verlag, 287–324.Google Scholar
11. Golas, A., Narain, R., Sewall, J., Krajcevski, P., Dubey, P., and Lin, M. 2012. Large-Scale Fluid Simulation using Velocity-Vorticity Domain Decomposition. ACM Trans. Graph. 31, 6. Google ScholarDigital Library
12. Governale, M., and Ungarelli, C. 1998. Gauge Invariant Grid Discretization of the Schrödinger Equation. Phys. Rev. B 58, 12, 7816–7821.Google ScholarCross Ref
13. Halvorsen, T. G., and Kvaal, S. 2012. Manifestly Gauge Invariant Discretizations of the Schrödinger Operator. Phys. Lett. A 376, 12–13, 1107–1114.Google Scholar
14. Jiang, M., Machiraju, R., and Thompson, D. 2005. Detection and Visualization of Vortices. In The Visualization Handbook, C. D. Hansen and C. R. Johnson, Eds. Elsevier, 295–309.Google Scholar
15. Kim, D., young Song, O., and Ko, H.-S. 2009. Stretching and Wiggling Liquids. ACM Trans. Graph. 28, 5. Google ScholarDigital Library
16. Kleckner, D., and Irvine, W. T. M. 2013. Creation and Dynamics of Knotted Vortices. Nat. Phys. 9, 4, 253–258.Google ScholarCross Ref
17. Knöppel, F., Crane, K., Pinkall, U., and Schröder, P. 2013. Globally Optimal Direction Fields. ACM Trans. Graph. 32, 4. Google ScholarDigital Library
18. Le, T. B., Borazjani, I., Kang, S., and Sotiropoulos, F. 2011. On the Structure of Vortex Rings from Inclined Nozzles. J. Fluid Mech. 686, 451–483.Google ScholarCross Ref
19. Museth, K. 2013. VDB: High-resolution Sparse Volumes with Dynamic Topology. ACM Trans. Graph. 32, 3, 27:1–27:22. Google ScholarDigital Library
20. Pfaff, T., Thuerey, N., and Gross, M. 2012. Lagrangian Vortex Sheets for Animating Fluids. ACM Trans. Graph. 31, 4. Google ScholarDigital Library
21. Saad, Y. 2005. ILUT: A Dual Threshold Incomplete LU Factorization. Num. Lin. Alg. Appl. 1, 4, 387–402.Google ScholarCross Ref
22. Side Effects Software Inc., 2013. Houdini#8482; FX.Google Scholar
23. Stathopoulos, A., and McCombs, J. R. 2010. PRIMME: PRe-conditioned Iterative MultiMethod Eigensolver: Methods and Software Description. ACM Trans. Math. Softw. 37, 2, 21:1–21:30. Google ScholarDigital Library
24. Stock, M. J., Dahm, W. J. A., and Tryggvason, G. 2008. Impact of a Vortex Ring on a Density Interface using a Regularized Inviscid Vortex Sheet Method. J. Comput. Phys. 227, 21, 9021–9043. Google ScholarDigital Library
25. Troolin, D. R., and Longmire, E. K. 2010. Volumetric Velocity Measurements of Vortex Rings from Inclined Exits. Exp. Fluids 48, 3, 409–420.Google ScholarCross Ref
26. Weißmann, S., and Pinkall, U. 2010. Filament-based Smoke with Vortex Shedding and Variational Reconnection. ACM Trans. Graph. 29, 4. Google ScholarDigital Library
27. Wikipedia, 2014. Hamiltonian (quantum mechanics) — Wikipedia, The Free Encyclopedia.Google Scholar
28. Wikipedia, 2014. Winding Number — Wikipedia, The Free Encyclopedia.Google Scholar
29. Wilson, K. G. 1974. Confinement of Quarks. Phys. Rev. D 10, 8, 2445–2459.Google ScholarCross Ref