“Self-organized criticality as a method of procedural modeling” by Pytel
Conference:
Type(s):
Title:
- Self-organized criticality as a method of procedural modeling
Presenter(s)/Author(s):
Abstract:
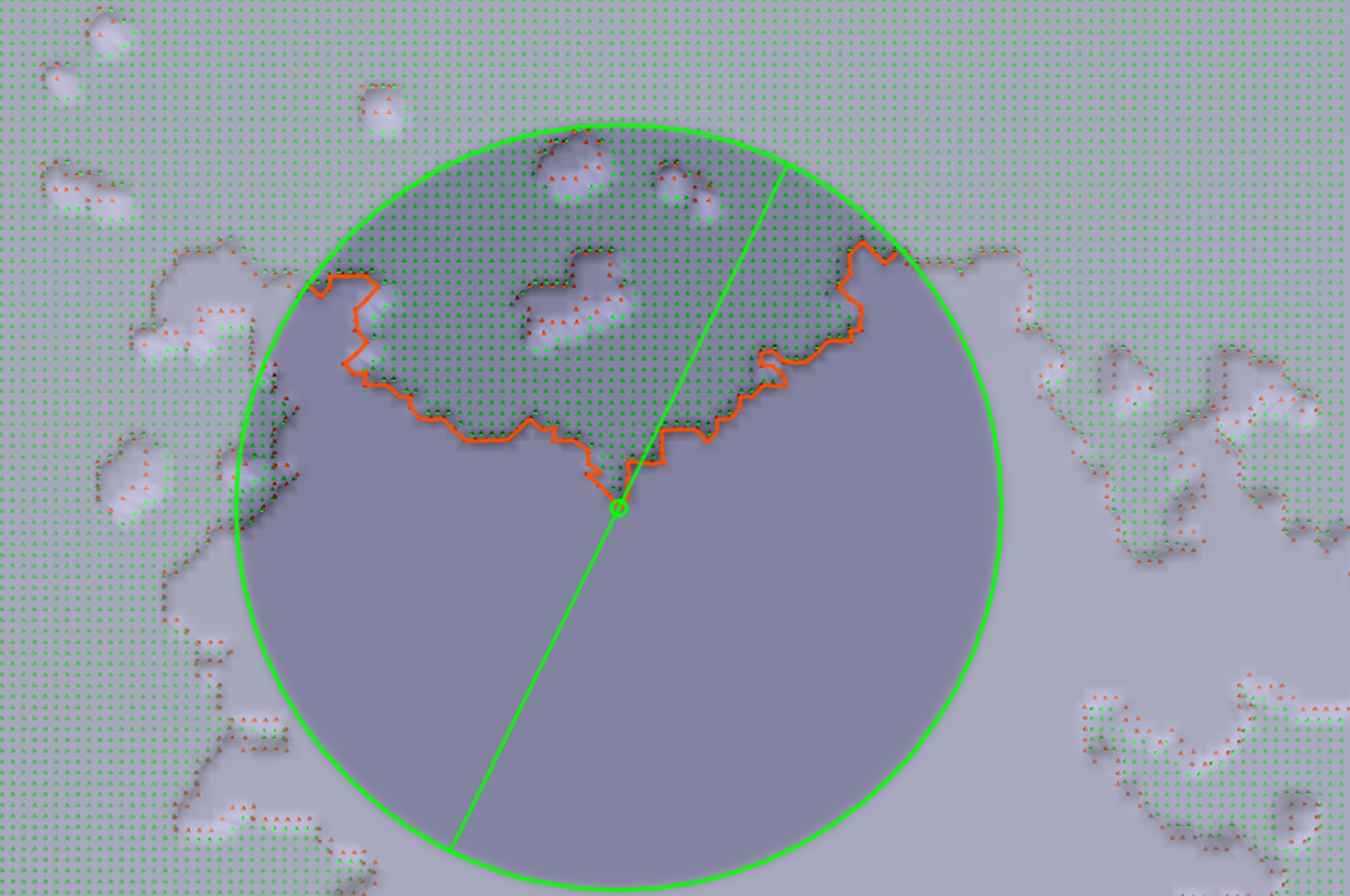
Self-organized criticality (SOC) is a theory of fractal dynamics in which a physical system approaches an attractor state that is scalefree. In the simple example of a sandpile, the grains of sand can slip down steep slopes and the resulting changes to the system propagate via avalanches. By the time the sandpile reaches the attractor state, the avalanches have propagated throughout the entire system and the features of the resulting landscape are not tied to a specific length scale.
References:
1. Ahlenius, H. 2007. Arctic Sea Ice Minimum Extent in September 1982 and 2008. UNEP/GRID-Arendal. http://maps.grida.no/go/graphic/.
2. Duran, J. 2000. Sands, Powders, and Grains: An Introduction to the Physics of Granular Materials. Partially Ordered Systems. Springer.
3. Maslanik, J., and Fowler, C. 2009. Arctic Sea Ice Age. University of Colorado.
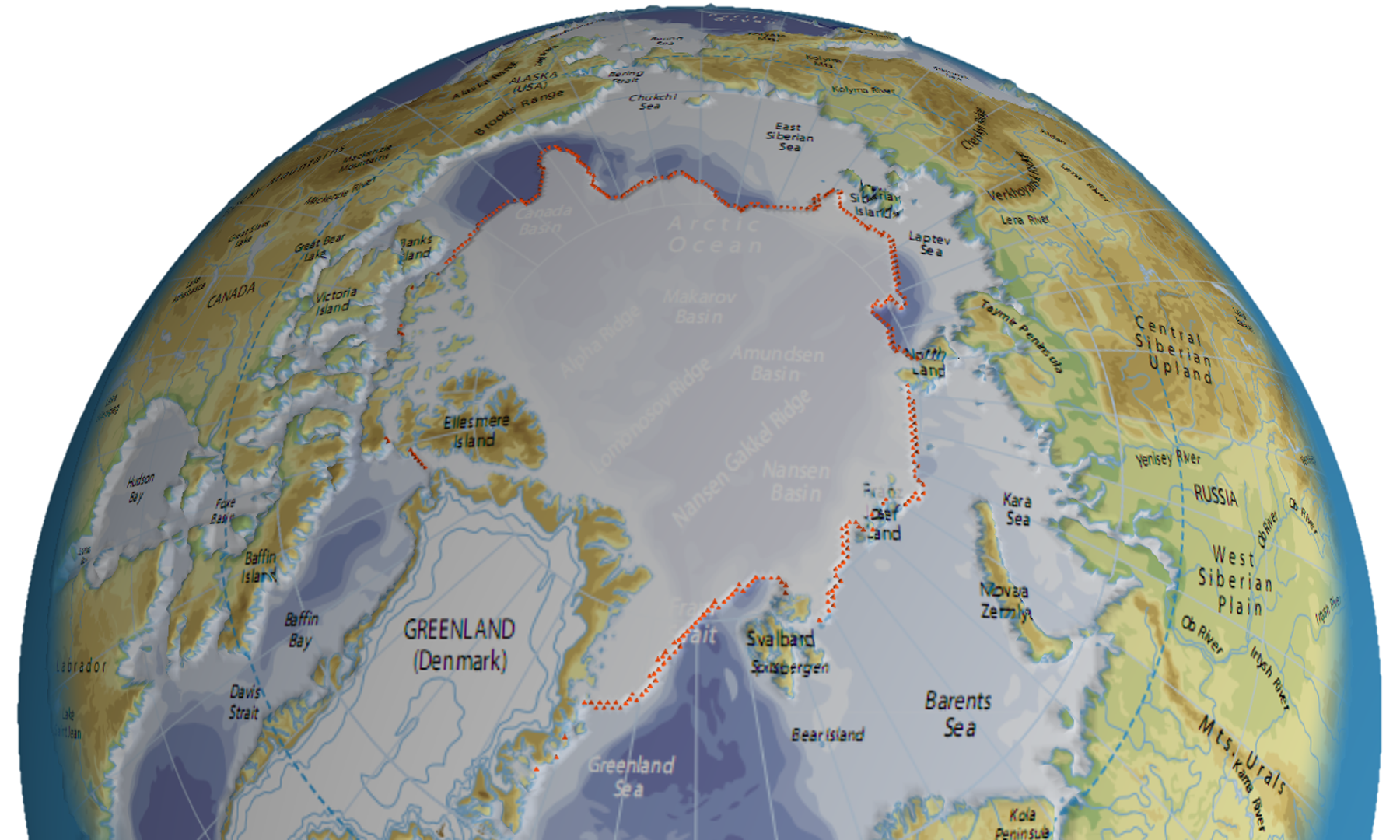
4. Rekacewicz, P. 2005. Arctic, Topography and Bathymetry. UNEP/GRID-Arendal. http://maps.grida.no/go/graphic/arctic-topography-and-bathymetry.
5. Rodríguez-Iturbe, I., and Rinaldo, A. 1997. Fractal River Basins. Cambridge University Press.
6. Sapoval, B., Baldassarri, A., and Gabrielli, A. 2004. Self-Stabilized Fractality of Seacoasts through Damped Erosion. Physical Review Letters 93, 9.
Additional Images: