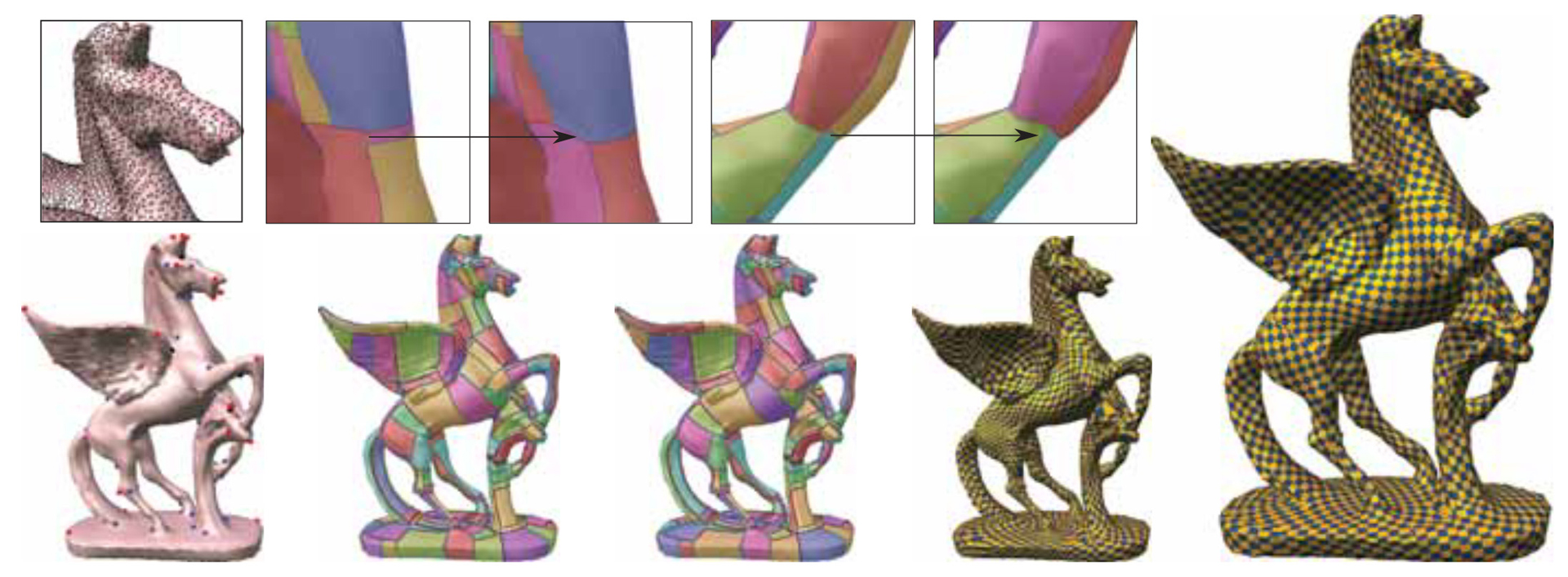
“Robust field-aligned global parametrization” by Myles, Pietroni and Zorin
Conference:
Type(s):
Title:
- Robust field-aligned global parametrization
Session/Category Title:
- Fields on Surfaces
Presenter(s)/Author(s):
Moderator(s):
Abstract:
We present a robust method for computing locally bijective global parametrizations aligned with a given cross-field. The singularities of the parametrization in general agree with singularities of the field, except in a small number of cases when several additional cones need to be added in a controlled way. Parametric lines can be constrained to follow an arbitrary set of feature lines on the surface. Our method is based on constructing an initial quad patch partition using robust cross-field integral line tracing. This process is followed by an algorithm modifying the quad layout structure to ensure that consistent parametric lengths can be assigned to the edges. For most meshes, the layout modification algorithm does not add new singularities; a small number of singularities may be added to resolve an explicitly described set of layouts. We demonstrate that our algorithm succeeds on a test data set of over a hundred meshes.
References:
1. Alliez, P., Cohen-Steiner, D., Devillers, O., Lévy, B., and Desbrun, M. 2003. Anisotropic polygonal remeshing. In ACM Transactions on Graphics (TOG), vol. 22, ACM, 485–493. Google ScholarDigital Library
2. Andronov, A. A., Leontovich, E., Gordon, I., and Maier, A. 1973. Qualitative theory of second-order dynamic systems. Israel Program for Scientific Translations Jerusalem.Google Scholar
3. Ben-Chen, M., Gotsman, C., and Bunin, G. 2008. Conformal flattening by curvature prescription and metric scaling. Computer Graphics Forum 27, 2, 449–458.Google ScholarCross Ref
4. Bommes, D., Zimmer, H., and Kobbelt, L. 2009. Mixed-integer quadrangulation. ACM Trans. Graph. 28, 3, 77. Google ScholarDigital Library
5. Bommes, D., Lvy, B., Pietroni, N., Puppo, E., Silva, C., Tarini, M., and Zorin, D. 2012. Quad Meshing. Eurographics Association, Cagliari, Sardinia, Italy, M.-P. Cani and F. Ganovelli, Eds., 159–182.Google Scholar
6. Bommes, D., Campen, M., Ebke, H.-C., Alliez, P., Kobbelt, L., et al. 2013. Integer-grid maps for reliable quad meshing. ACM Trans. Graph. 32, 4. Google ScholarDigital Library
7. Dong, S., Bremer, P., Garland, M., Pascucci, V., and Hart, J. 2006. Spectral surface quadrangulation. ACM Trans. Graph. 25, 3, 1057–1066. Google ScholarDigital Library
8. Eppstein, D., and Erickson, J. 1999. Raising roofs, crashing cycles, and playing pool: Applications of a data structure for finding pairwise interactions. Discrete and Computational Geometry 22, 4, 569–592.Google ScholarCross Ref
9. Eppstein, D., Goodrich, M. T., Kim, E., and Tamstorf, R. 2008. Motorcycle graphs: canonical quad mesh partitioning. In Computer Graphics Forum, vol. 27, Wiley Online Library, 1477–1486. Google ScholarDigital Library
10. Gunpinar, E., Moriguchi, M., Suzuki, H., and Ohtake, Y. 2014. Feature-aware partitions from the motorcycle graph. Computer-Aided Design 47, 85–95. Google ScholarDigital Library
11. Jadhav, S., Bhatia, H., Bremer, P.-T., Levine, J. A., Nonato, L. G., and Pascucci, V. 2012. Consistent approximation of local flow behavior for 2d vector fields using edge maps. In Topological Methods in Data Analysis and Visualization II. Springer, 141–159.Google Scholar
12. Kharevych, L., Springborn, B., and Schröder, P. 2006. Discrete conformal mappings via circle patterns. ACM Trans. Graph. 25 (April), 412–438. Google ScholarDigital Library
13. Knöppel, F., Crane, K., Pinkall, U., and Schröder, P. 2013. Globally optimal direction fields. ACM Transactions on Graphics (TOG) 32, 4, 59. Google ScholarDigital Library
14. Lee, A., Sweldens, W., Schröder, P., Cowsar, L., and Dobkin, D. 1998. MAPS: multiresolution adaptive parameterization of surfaces. In SIGGRAPH 1998, 95–104. Google ScholarDigital Library
15. Li, W.-C., Vallet, B., Ray, N., and Lévy, B. 2006. Representing higher-order singularities in vector fields on piecewise linear surfaces. Visualization and Computer Graphics, IEEE Transactions on 12, 5, 1315–1322. Google ScholarDigital Library
16. Li, W., Ray, N., and Lévy, B. 2006. Automatic and interactive mesh to T-spline conversion. In Symposium on Geometry Processing, Eurographics Association, 200. Google ScholarDigital Library
17. Lipman, Y. 2012. Bounded distortion mapping spaces for triangular meshes. ACM Transactions on Graphics (TOG) 31, 4, 108. Google ScholarDigital Library
18. Myles, A., and Zorin, D. 2012. Global parametrization by incremental flattening. ACM Transactions on Graphics (TOG) 31, 4, 109. Google ScholarDigital Library
19. Myles, A., and Zorin, D. 2013. Controlled-distortion constrained global parametrization. ACM Transactions on Graphics (TOG) 32, 4, 105. Google ScholarDigital Library
20. Myles, A., Pietroni, N., Kovacs, D., and Zorin, D. 2010. Feature-aligned T-meshes. ACM Trans. Graph. 29, 4, 1–11. Google ScholarDigital Library
21. Ray, N., and Sokolov, D. 2013. Tracing cross-free polylines oriented by a n-symmetry direction field on triangulated surfaces. arXiv preprint arXiv:1306.0706.Google Scholar
22. Ray, N., Li, W., Lévy, B., Sheffer, A., and Alliez, P. 2006. Periodic global parameterization. ACM Trans. Graph. 25, 4, 1460–1485. Google ScholarDigital Library
23. Ray, N., Vallet, B., Li, W., and Lévy, B. 2008. N-Symmetry direction field design. ACM Trans. Graph. 27, 2. Google ScholarDigital Library
24. Sheffer, A., and de Sturler, E. 2001. Parameterization of Faceted Surfaces for Meshing using Angle-Based Flattening. Engineering with Computers 17, 3, 326–337.Google ScholarCross Ref
25. Springborn, B., Schröder, P., and Pinkall, U. 2008. Conformal equivalence of triangle meshes. ACM Trans. Graph. 27 (August), 77:1–77:11. Google ScholarDigital Library
26. Szymczak, A., and Zhang, E. 2012. Robust morse decompositions of piecewise constant vector fields. Visualization and Computer Graphics, IEEE Transactions on 18, 6, 938–951. Google ScholarDigital Library
27. Tong, Y., Alliez, P., Cohen-Steiner, D., and Desbrun, M. 2006. Designing quadrangulations with discrete harmonic forms. Symposium on Geometry Processing, 201–210. Google ScholarDigital Library
28. Tricoche, X., Scheuermann, G., and Hagen, H. 2000. Higher order singularities in piecewise linear vector fields. In The Mathematics of Surfaces IX. Springer, 99–113. Google ScholarDigital Library
29. Tricoche, X. 2002. Vector and tensor field topology simplification, tracking, and visualization. In PhD. thesis, Universität Kaiserslautern, Citeseer.Google Scholar
30. Zhang, E., Mischaikow, K., and Turk, G. 2006. Vector field design on surfaces. ACM Transactions on Graphics (TOG) 25, 4, 1294–1326. Google ScholarDigital Library