“Multiresolution analysis of arbitrary meshes” by Eck, DeRose, Duchamp, Hoppe, Lounsbery, et al. …

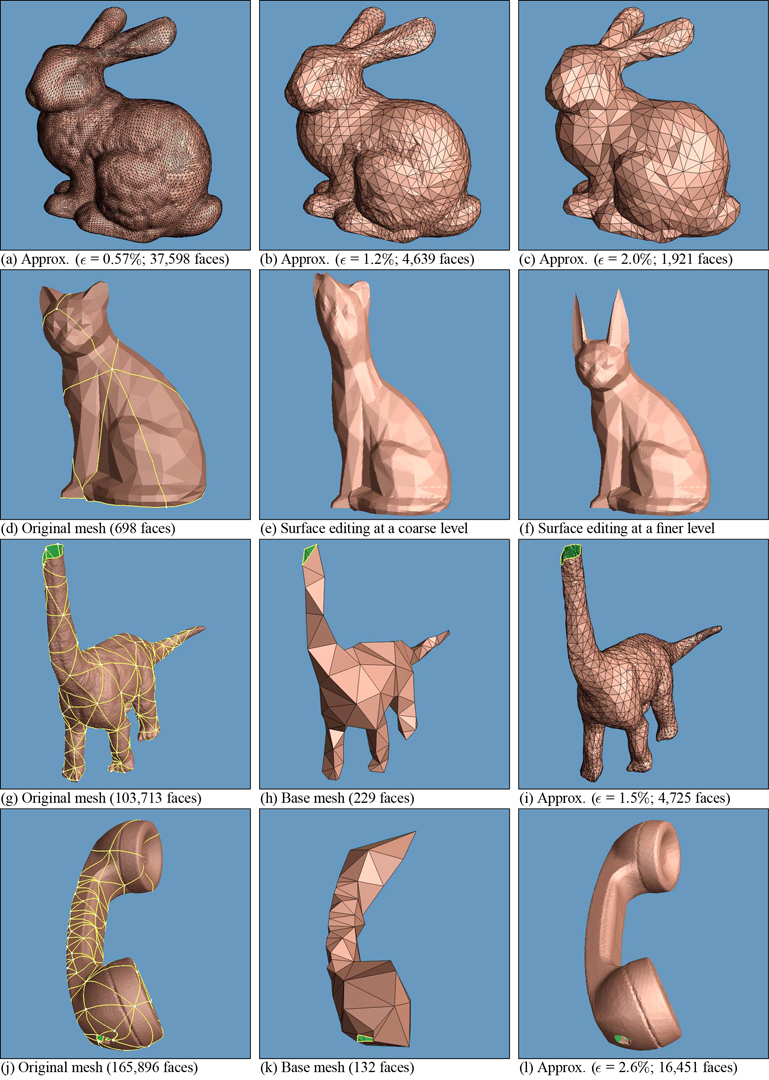
In computer graphics and geometric modeling, shapes are often represented by triangular meshes. With the advent of laser scanning systems, meshes of extreme complexity are rapidly becoming commonplace. Such meshes are notoriously expensive to store, transmit, render, and are awkward to edit. Multiresolution analysis offers a simple, unified, and theoretically sound approach to dealing with these problems. Lounsbery et al. have recently developed a technique for creating multiresolution representations for a restricted class of meshes with subdivision connectivity. Unfortunately, meshes encountered in practice typically do not meet this requirement. In this paper we present a method for overcoming the subdivision connectivity restriction, meaning that completely arbitrary meshes can now be converted to multiresolution form. The method is based on the approximation of an arbitrary initial mesh M by a mesh MJ that has subdivision connectivity and is guaranteed to be within a specified tolerance. The key ingredient of our algorithm is the construction of a parametrization of M over a simple domain. We expect this parametrization to be of use in other contexts, such as texture mapping or the approximation of complex meshes by NURBS patches.

1. A. Aho, J.E. Hopcroft, and J.D. Ullman. Data structures and algorithms. Addison-Wesley, Reading, Mass., 1983.
2. J. Eells and L. Lemaire. Another report on harmonic maps. Bull. London Math. Soc., 20:385-524, 1988.
3. J. Eells and J.H. Sampson. Harmonic mappings of Riemannian manifolds. Amer. J. Math., 86:109-160, 1964.
4. Adam Finkelstein and David Salesin. Multiresolution curves. Computer Graphics (SIGGRAPH ’94 Proceedings), 28(3):261-268, July 1994.
5. D. Forsey and R. Bartels. Hierarchical B-spline fitting. ACM Transactions on Graphics. To appear.
6. D. Forsey and R. Bartels. Hierarchical B-spline refinement. Computer Graphics, 22(4):205-212, 1988.
7. David Forsey and Lifeng Wang. Multi-resolution surface approximation for animation. In Proceedings of Graphics Interface, 1993.
8. H. Hoppe, T. DeRose, T. Duchamp, J. McDonald, and W. Stuetzle. Mesh optimization. Computer Graphics (SIGGRAPH ’93 Proceedings), pages 19-26, August 1993.
9. James R. Kent, Wayne E. Carlson, and Richard E. Parent. Shape transformation for polyhedral objects. Computer Graphics (SIGGRAPH ’92 Proceedings), 26(2):47-54, July 1992.
10. J. Michael Lounsbery. Multiresolution Analysis for Surfaces of Arbitrary Topological Type. PhD thesis, Department of Computer Science and Engineering, University of Washington, September 1994. Available as ftp://cs.washington.edu/pub/graphics/LounsPhd.ps.Z.
11. Michael Lounsbery, Tony DeRose, and Joe Warren. Multiresolution analysis for surfaces of arbitrary topological type. Submitted for publication. Preliminary version available as Technical Report 93-10-05b, Department of Computer Science and Engineering, University of Washington, January, 1994. Also available as ftp://cs.washington.edu/pub/graphics/TR931005b.ps.Z.
12. J. Maillot, H. Yahia, and A. Verroust. Interactive texture mapping. Computer Graphics (SIGGRAPH ’93 Proceedings), 27(3):27-34, August 1993.
13. Stephane Mallat. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11 (7):674-693, July 1989.
14. J.S. Mitchell, D.M. Mount, and C.H. Papadimitriou. The discrete geodesic problem. SlAM Journal of Computing, 16(4):647-668, 1987.
15. David M. Mount. Voronoi diagrams on the surface of a polyhedron. Department of Computer Science CAR-TR-121, CS-TR-1496, University of Maryland, May 1985.
16. J. Rossignac and R Borrel. Multi-resolution 3D approximations for rendering. In B. Falcidieno and T.L. Kunii, editors, Modeling in Computer Graphics, pages 455-465. Springer-Verlag, June-July 1993.
17. Richard Schoen and Shing-Tung Yau. Univalent harmonic maps between surfaces. Inventiones math., 44:265-278, 1978.
18. R Schr6der and W. Sweldens. Spherical wavelets: Efficiently representing functions on the sphere. Computer Graphics, (SIGGRAPH’95 Proceedings), 1995.
19. William Schroeder, Jonathan Zarge, and William Lorensen. Decimation of triangle meshes. Computer Graphics (SIGGRAPH ’92 Proceedings), 26(2):65-70, July 1992.
20. Greg Turk. Re-tiling polygonal surfaces. Computer Graphics (SIG- GRAPH ’92 Proceedings), 26(2):55-64, July 1992.
21. Greg Turk and Marc Levoy. Zippered polygon meshes from range images. Computer Graphics (SIGGRAPH ’94 Proceedings), 28(3):311- 318, July 1994.
22. Amitabh Varshney. Hierarchical Geometric Approximations. PhD thesis, Department of Computer Science, University of North Carolina at Chapel Hill, 1994.