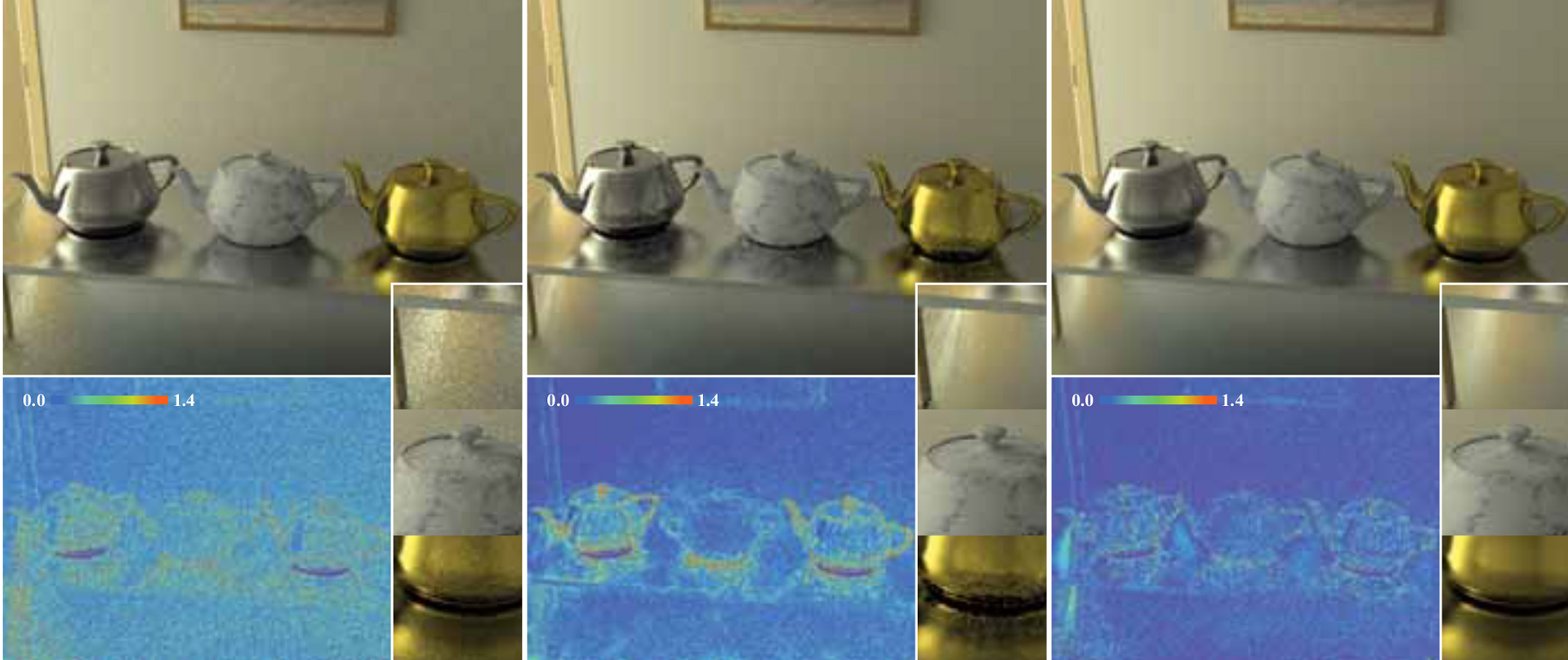
“Multiplexed metropolis light transport” by Hachisuka, Kaplanyan and Dachsbacher
Conference:
Type(s):
Title:
- Multiplexed metropolis light transport
Session/Category Title: Light Transport
Presenter(s)/Author(s):
Moderator(s):
Abstract:
Global illumination algorithms using Markov chain Monte Carlo (MCMC) sampling are well-known for their efficiency in scenes with complex light transport. Samples in such algorithms are generated as a history of Markov chain states so that they are distributed according to the contributions to the image. The whole process is done based only on the information of the path contributions and user-defined transition probabilities from one state to the others. In light transport simulation, however, there is more information that can be used to improve the efficiency of path sampling. A notable example is multiple importance sampling (MIS) in bidirectional path tracing, which utilizes the probability densities of constructing a given path with different estimators. While MIS is a powerful ordinary Monte Carlo method, how to incorporate such additional information into MCMC sampling has been an open problem. We introduce a novel MCMC sampling framework, primary space serial tempering, which fuses the ideas of MCMC sampling and MIS for the first time. The key idea is to explore not only the sample space using a Markov chain, but also different estimators to generate samples by utilizing the information already available for MIS. Based on this framework, we also develop a novel rendering algorithm, multiplexed Metropolis light transport, which automatically and adaptively constructs paths with appropriate techniques as predicted by MIS. The final algorithm is very easy to implement, yet in many cases shows comparable (or even better) performance than significantly more complex MCMC rendering algorithms.
References:
1. Arvo, J. 1986. Backward ray tracing. In Developments in Ray Tracing, ACM SIGGRAPH Course Notes, 259–263.Google Scholar
2. Bouchard, G., Iehl, J.-C., Ostromoukhov, V., and Poulin, P. 2013. Improving Robustness of Monte-Carlo Global Illumination with Directional Regularization. In SIGGRAPH Asia Technical Briefs, 22:1–22:4. Google ScholarDigital Library
3. Brooks, S., Gelman, A., Jones, G., and Meng, X.-L. 2011. Handbook of Markov Chain Monte Carlo. Taylor & Francis US.Google Scholar
4. Chen, J., Wang, B., and Yong, J.-H. 2011. Improved stochastic progressive photon mapping with Metropolis sampling. Computer Graphics Forum 30, 4, 1205–1213. Google ScholarDigital Library
5. Cline, D., Talbot, J., and Egbert, P. K. 2005. Energy redistribution path tracing. ACM Transactions on Graphics (Proc. SIGGRAPH) 24, 3, 1186–1195. Google ScholarDigital Library
6. Georgiev, I., Křivánek, J., Davidovič, T., and Slusallek, P. 2012. Light transport simulation with vertex connection and merging. ACM Transactions on Graphics (Proc. SIGGRAPH Asia) 31, 6, 192:1–192:10. Google ScholarDigital Library
7. Geyer, C. J., and Thompson, E. A. 1995. Annealing Markov chain Monte Carlo with applications to ancestral inference. Journal of the American Statistical Association 90, 431, 909–920.Google ScholarCross Ref
8. Hachisuka, T., and Jensen, H. W. 2009. Stochastic progressive photon mapping. ACM Transactions on Graphics (Proc. SIGGRAPH Asia) 28, 5, 141:1–141:8. Google ScholarDigital Library
9. Hachisuka, T., and Jensen, H. W. 2011. Robust adaptive photon tracing using photon path visibility. ACM Transactions on Graphics 30, 5, 114:1–114:11. Google ScholarDigital Library
10. Hachisuka, T., Ogaki, S., and Jensen, H. W. 2008. Progressive photon mapping. ACM Transactions on Graphics (Proc. SIGGRAPH Asia) 27, 5, 130. Google ScholarDigital Library
11. Hachisuka, T., Pantaleoni, J., and Jensen, H. W. 2012. A path space extension for robust light transport simulation. ACM Transactions on Graphics (Proc. SIGGRAPH Asia) 31, 6, 191:1–191:10. Google ScholarDigital Library
12. Hastings, W. K. 1970. Monte Carlo sampling methods using Markov chains and their applications. Biometrika 57, 1, 97–109.Google ScholarCross Ref
13. Jakob, W., and Marschner, S. 2012. Manifold exploration: a Markov chain Monte Carlo technique for rendering scenes with difficult specular transport. ACM Transactions on Graphics (Proc. SIGGRAPH) 31, 4, 58:1–58:13. Google ScholarDigital Library
14. Jakob, W., 2010. Mitsuba renderer. http://www.mitsuba-renderer.org.Google Scholar
15. Jensen, H. W. 1996. Global illumination using photon maps. In Proc. Eurographics Workshop on Rendering, 21–30. Google ScholarDigital Library
16. Kajiya, J. T. 1986. The rendering equation. Computer Graphics (Proceedings of SIGGRAPH ’86), 143–150. Google ScholarDigital Library
17. Kaplanyan, A. S., and Dachsbacher, C. 2013. Path space regularization for holistic and robust light transport. Computer Graphics Forum (Proc. of Eurographics) 32, 2.Google ScholarCross Ref
18. Kelemen, C., Szirmay-Kalos, L., Antal, G., and Csonka, F. 2002. A simple and robust mutation strategy for the Metropolis light transport algorithm. Computer Graphics Forum 21, 3, 531–540.Google ScholarCross Ref
19. Kitaoka, S., Kitamura, Y., and Kishino, F. 2009. Replica exchange light transport. Computer Graphics Forum 28, 8, 2330–2342.Google ScholarCross Ref
20. Lafortune, E. P., and Willems, Y. D. 1993. Bi-directional path tracing. In Compugraphics ’93, 145–153.Google Scholar
21. Lai, Y.-C., Fan, S. H., Chenney, S., and Dyer, C. 2007. Photorealistic image rendering with population Monte Carlo energy redistribution. In In Rendering Techniques 2007 (Proceedings of the Eurographics Symposium on Rendering), 287–295. Google ScholarDigital Library
22. Lehtinen, J., Karras, T., Laine, S., Aittala, M., Durand, F., and Aila, T. 2013. Gradient-domain Metropolis light transport. ACM Transactions on Graphics (Proc. SIGGRAPH) 32, 4. Google ScholarDigital Library
23. Marinari, E., and Parisi, G. 1992. Simulated tempering: a new Monte Carlo scheme. EPL (Europhysics Letters) 19, 6, 451.Google ScholarCross Ref
24. Metropolis, N., and Ulam, S. 1949. The Monte Carlo method. Journal of the American Statistical Association 44, 247, 335–341.Google ScholarCross Ref
25. Metropolis, N., Rosenbluth, A. W., Rosenbluth, M. N., Teller, A. H., and Teller, E. 1953. Equation of state calculations by fast computing machines. The Journal of Chemical Physics 21, 1087.Google ScholarCross Ref
26. Swendsen, R. H., and Wang, J.-S. 1986. Replica Monte Carlo simulation of spin glasses. Physical Review Letters 57, 21, 2607–2609.Google ScholarCross Ref
27. Veach, E., and Guibas, L. J. 1995. Optimally combining sampling techniques for Monte Carlo rendering. In SIGGRAPH ’95, 419–428. Google ScholarDigital Library
28. Veach, E., and Guibas, L. 1997. Metropolis light transport. In SIGGRAPH ’97, 65–76. Google ScholarDigital Library
29. Veach, E. 1998. Robust Monte Carlo methods for light transport simulation. PhD thesis, Stanford University, USA. AAI9837162. Google ScholarDigital Library
30. Walter, B., Khungurn, P., and Bala, K. 2012. Bidirectional lightcuts. ACM Transactions on Graphics (Proc. SIGGRAPH) 31, 4, 59:1–59:11. Google ScholarDigital Library
31. Zsolnai, K., and Szirmay-Kalos, L. 2013. Automatic parameter control for Metropolis light transport. In Eurographics short papers, 53–56.Google Scholar