“MOCCA: modeling and optimizing cone-joints for complex assemblies” by Wang, Song and Pauly

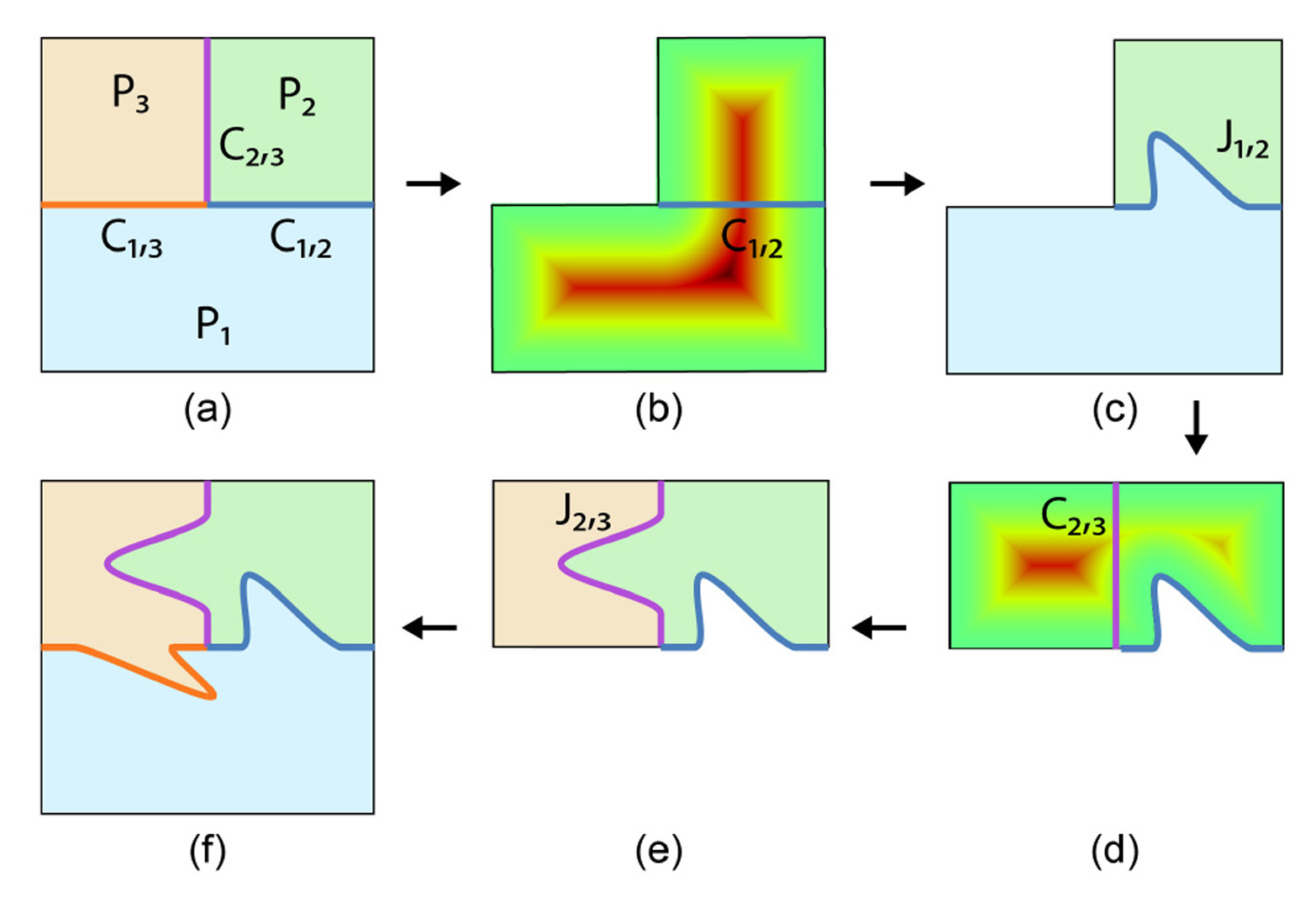
We present a computational framework for modeling and optimizing complex assemblies using cone joints. Cone joints are integral joints that generalize traditional single-direction joints such as mortise and tenon joints to support a general cone of directions for assembly. This additional motion flexibility not just reduces the risk of deadlocking for complex joint arrangements, but also simplifies the assembly process, in particular for automatic assembly by robots. On the other hand, compared to planar contacts, cone joints restrict relative part movement for improved structural stability. Cone joints can be realized in the form of curved contacts between associated parts, which have demonstrated good mechanical properties such as reduced stress concentration. To find the best trade-off between assemblability and stability, we propose an optimization approach that first determines the optimal motion cone for each part contact and subsequently derives a geometric realization of each joint to match this motion cone. We demonstrate that our approach can optimize cone joints for assemblies with a variety of geometric forms, and highlight several application examples.

1. Ergun Akleman, Vinayak R. Krishnamurthy, Chia-An Fu, Sai Ganesh Subramanian, Matthew Ebert, Matthew Eng, Courtney Starrett, and Haard Panchal. 2020. Generalized Abeille Tiles: Topologically Interlocked Space-filling Shapes Generated Based on Fabric Symmetries. Comp. & Graph. (SMI) 89 (2020), 156–166.Google ScholarCross Ref
2. Chrystiano Araújo, Daniela Cabiddu, Marco Attene, Marco Livesu, Nicholas Vining, and Alla Sheffer. 2019. Surface2Volume: Surface Segmentation Conforming Assemblable Volumetric Partition. ACM Trans. on Graph. (SIGGRAPH) 38, 4 (2019), 1:1–1:16.Google ScholarDigital Library
3. Artelys. 2020. Knitro software package. https://www.artelys.com/solvers/knitro/.Google Scholar
4. Philippe Block and John Ochsendorf. 2007. Thrust Network Analysis: A New Methodology for Three-dimensional Equilibrium. Journal of the International Association for Shell and Spatial Structures 48, 3 (2007), 167–173.Google Scholar
5. Stephen Boyd and Lieven Vandenberghe. 2004. Convex Optimization. Cambridge University Press.Google ScholarDigital Library
6. Paolo Cignoni, Nico Pietroni, Luigi Malomo, and Roberto Scopigno. 2014. Field-aligned Mesh Joinery. ACM Trans. on Graph. 33, 1 (2014), 11:1–11:12.Google ScholarDigital Library
7. Ruta Desai, James McCann, and Stelian Coros. 2018. Assembly-aware Design of Printable Electromechanical Devices. In Proc. ACM UIST. 457–472.Google ScholarDigital Library
8. Mario Deuss, Daniele Panozzo, Emily Whiting, Yang Liu, Philippe Block, Olga Sorkine-Hornung, and Mark Pauly. 2014. Assembling Self-Supporting Structures. ACM Trans. on Graph. (SIGGRAPH Asia) 33, 6 (2014), 214:1–214:10.Google ScholarDigital Library
9. Simon Duenser, Roi Poranne, Bernhard Thomaszewski, and Stelian Coros. 2020. Robo-Cut: Hot-wire Cutting with Robot-controlled Flexible Rods. ACM Trans. on Graph. (SIGGRAPH) 39, 4 (2020), 98:1–98:15.Google ScholarDigital Library
10. A. V. Dyskin, Yuri Estrin, and E. Pasternak. 2019. Topological Interlocking Materials. In Architectured Materials in Nature and Engineering, Yuri Estrin, Yves Bréchet, John Dunlop, and Peter Fratzl (Eds.). Springer International Publishing, Chapter 2, 23–49.Google Scholar
11. A. V. Dyskin, Y. Estrin, E. Pasternak, H. C. Khor, and A. J. Kanel-Belov. 2003. Fracture Resistant Structures Based on Topological Interlocking with Non-planar Contacts. Advanced Engineering Materials 5, 3 (2003), 116–119.Google ScholarCross Ref
12. William Fairham. 2013. Woodwork Joints: How to Make and Where to Use Them. Sky-horse.Google Scholar
13. Giuseppe Fallacara, Maurizio Barberio, and Micaela Colella. 2019. Topological Interlocking Blocks for Architecture: From Flat to Curved Morphologies. In Architectured Materials in Nature and Engineering, Yuri Estrin, Yves Bréchet, John Dunlop, and Peter Fratzl (Eds.). Springer International Publishing, Chapter 14, 423–445.Google Scholar
14. Julius Farkas. 1902. Theorie der Einfachen Ungleichungen. Journal für die Reine und Angewandte Mathematik 124 (1902), 1–27.Google Scholar
15. Chi-Wing Fu, Peng Song, Xiaoqi Yan, Lee Wei Yang, Pradeep Kumar Jayaraman, and Daniel Cohen-Or. 2015. Computational Interlocking Furniture Assembly. ACM Trans. on Graph. (SIGGRAPH) 34, 4 (2015), 91:1–91:11.Google ScholarDigital Library
16. Somayé Ghandi and Ellips Masehian. 2015. Review and Taxonomies of Assembly and Disassembly Path Planning Problems and Approaches. Computer-Aided Design 67-68 (2015), 58–86.Google Scholar
17. Jingbin Hao, Liang Fang, and Robert E. Williams. 2011. An Efficient Curvature-based Partitioning of Large-scale STL Models. Rapid Prototyping Journal 17, 2 (2011), 116–127.Google ScholarCross Ref
18. Kristian Hildebrand, Bernd Bickel, and Marc Alexa. 2012. crdbrd: Shape Fabrication by Sliding Planar Slices. Comp. Graph. Forum (Eurographics) 31, 2 (2012), 583–592.Google ScholarDigital Library
19. Alec Jacobson, Daniele Panozzo, et al. 2018. libigl: A simple C++ geometry processing library. https://libigl.github.io/.Google Scholar
20. Anooshe Rezaee Javan, Hamed Seifi, Shanqing Xu, and Yi Min Xie. 2016. Design of A New Type of Interlocking Brick and Evaluation of Its Dynamic Performance. In Proceedings of the International Association for Shell and Spatial Structures Annual Symposium. 1–8.Google Scholar
21. Gene T.C. Kao, Axel Kórner, Daniel Sonntag, Long Nguyen, Achim Menges, and Jan Knippers. 2017. Assembly-aware Design of Masonry Shell Structures: A Computational Approach. In Proceedings of the International Association for Shell and Spatial Structures Symposium.Google Scholar
22. Lydia Kavraki, Jean-Claude Latombe, and Randall H.Wilson. 1993. On the Complexity of Assembly Partitioning. Inform. Process. Lett. 48, 5 (1993), 229–235.Google ScholarDigital Library
23. Vinayak R. Krishnamurthy, Ergun Akleman, Sai Ganesh Subramanian, Katherine Boyd, Chia-An Fu, Matthew Ebert, Courtney Starrett, and Neeraj Yadav. 2020. Bi-Axial Woven Tiles: Interlocking Space-Filling Shapes Based on Symmetries of Bi-Axial Weaving Patterns. In Proc. Graphics Interface. 286–298.Google Scholar
24. Maria Larsson, Hironori Yoshida, Nobuyuki Umetani, and Takeo Igarashi. 2020. Tsugite: Interactive Design and Fabrication of Wood Joints. In Proc. ACM UIST. 317–327.Google ScholarDigital Library
25. Kui-Yip Lo, Chi-Wing Fu, and Hongwei Li. 2009. 3D Polyomino Puzzle. ACM Trans. on Graph. (SIGGRAPH Asia) 28, 5 (2009), 157:1–157:8.Google Scholar
26. Linjie Luo, Ilya Baran, Szymon Rusinkiewicz, and Wojciech Matusik. 2012. Chopper: Partitioning Models into 3D-printable Parts. ACM Trans. on Graph. (SIGGRAPH Asia) 31, 6 (2012), 129:1–129:9.Google Scholar
27. Sheng-Jie Luo, Yonghao Yue, Chun-Kai Huang, Yu-Huan Chung, Sei Imai, Tomoyuki Nishita, and Bing-Yu Chen. 2015. Legolization: Optimizing LEGO Designs. ACM Trans. on Graph. (SIGGRAPH Asia) 34, 6 (2015), 222:1–222:12.Google ScholarDigital Library
28. Renato D. C. Monteiro and Ilan Adler. 1989. Interior Path Following Primal-dual Algorithms. Part II: Convex Quadratic Programming. Mathematical Programming 44 (1989), 43–66.Google ScholarDigital Library
29. Daniele Panozzo, Philippe Block, and Olga Sorkine-Hornung. 2013. Designing Unreinforced Masonry Models. ACM Trans. on Graph. (SIGGRAPH) 32, 4 (2013), 91:1–91:11.Google ScholarDigital Library
30. Yuliy Schwartzburg and Mark Pauly. 2013. Fabrication-aware Design with Intersecting Planar Pieces. Comp. Graph. Forum (Eurographics) 32, 2 (2013), 317–326.Google ScholarCross Ref
31. Hijung V. Shin, Christopher F. Porst, Etienne Vouga, John Ochsendorf, and Frédo Durand. 2016. Reconciling Elastic and Equilibrium Methods for Static Analysis. ACM Trans. on Graph. 35, 2 (2016), 13:1–13:16.Google ScholarDigital Library
32. Peng Song, Bailin Deng, Ziqi Wang, Zhichao Dong, Wei Li, Chi-Wing Fu, and Ligang Liu. 2016. CofiFab: Coarse-to-Fine Fabrication of Large 3D Objects. ACM Trans. on Graph. (SIGGRAPH) 35, 4 (2016), 45:1–45:11.Google ScholarDigital Library
33. Peng Song, Chi-Wing Fu, and Daniel Cohen-Or. 2012. Recursive Interlocking Puzzles. ACM Trans. on Graph. (SIGGRAPH Asia) 31, 6 (2012), 128:1–128:10.Google ScholarDigital Library
34. Peng Song, Chi-Wing Fu, Yueming Jin, Hongfei Xu, Ligang Liu, Pheng-Ann Heng, and Daniel Cohen-Or. 2017. Reconfigurable Interlocking Furniture. ACM Trans. on Graph. (SIGGRAPH Asia) 36, 6 (2017), 174:1–174:14.Google Scholar
35. Sai Ganesh Subramanian, Mathew Eng, Vinayak R. Krishnamurthy, and Ergun Akleman. 2019. Delaunay Lofts: A Biologically Inspired Approach for Modeling Space Filling Modular Structures. Comp. & Graph. (SMI) 82 (2019), 73–83.Google ScholarDigital Library
36. Ziqi Wang, Peng Song, Florin Isvoranu, and Mark Pauly. 2019. Design and Structural Optimization of Topological Interlocking Assemblies. ACM Trans. on Graph. (SIGGRAPH Asia) 38, 6 (2019), 193:1–193:13.Google Scholar
37. Ziqi Wang, Peng Song, and Mark Pauly. 2018. DESIA: A General Framework for Designing Interlocking Assemblies. ACM Trans. on Graph. (SIGGRAPH Asia) 37, 6 (2018), 191:1–191:14.Google Scholar
38. Ziqi Wang, Peng Song, and Mark Pauly. 2021. State of the Art on Computational Design of Assemblies with Rigid Parts. Comp. Graph. Forum (Eurographics) 40, 2 (2021).Google Scholar
39. Michael Weizmann, Oded Amir, and Yasha Jacob Grobman. 2017. Topological Interlocking in Architecture: A New Design Method and Computational Tool for Designing Building Floors. International Journal of Architectural Computing 15, 2 (2017), 107–118.Google ScholarCross Ref
40. Emily Whiting, John Ochsendorf, and Frédo Durand. 2009. Procedural Modeling of Structurally-Sound Masonry Buildings. ACM Trans. on Graph. (SIGGRAPH Asia) 28, 5 (2009), 112:1–112:9.Google Scholar
41. Emily Whiting, Hijung Shin, Robert Wang, John Ochsendorf, and Frédo Durand. 2012. Structural Optimization of 3D Masonry Buildings. ACM Trans. on Graph. (SIGGRAPH Asia) 31, 6 (2012), 159:1–159:11.Google Scholar
42. Randall H. Wilson and Toshihiro Matsui. 1992. Partitioning an Assembly for Infinitesimal Motions in Translation and Rotation. In IEEE/RSJ Intl. Conf. on Intelligent Robots and Systems. 1311–1318.Google Scholar
43. Wenzheng Xu, Xiaoshan Lin, and Yi Min Xie. 2020. A Novel Non-planar Interlocking Element for Tubular Structures. Tunnelling and Underground Space Technology 103 (2020). Article No. 103503.Google Scholar
44. Jiaxian Yao, Danny M. Kaufman, Yotam Gingold, and Maneesh Agrawala. 2017b. Interactive Design and Stability Analysis of Decorative Joinery for Furniture. ACM Trans. on Graph. 36, 2 (2017), 20:1–20:16.Google ScholarDigital Library
45. Miaojun Yao, Zhili Chen, Weiwei Xu, and Huamin Wang. 2017a. Modeling, Evaluation and Optimization of Interlocking Shell Pieces. Comp. Graph. Forum (Pacific Graphics) 36, 7 (2017), 1–13.Google ScholarCross Ref
46. Yinan Zhang, Yotto Koga, and Devin Balkcom. 2021. Interlocking Block Assembly With Robots. IEEE Transactions on Automation Science and Engineering (2021). online article.Google ScholarCross Ref