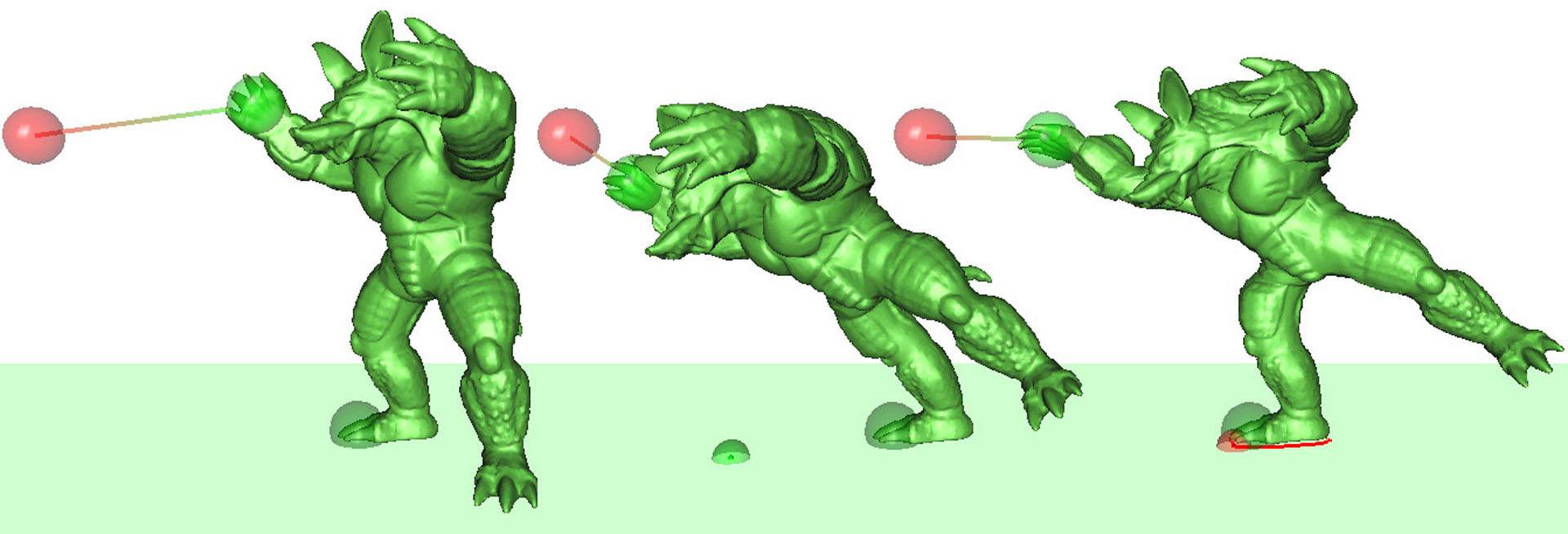
“Mesh puppetry: cascading optimization of mesh deformation with inverse kinematics” by Shi, Zhou, Tong, Desbrun, Bao, et al. …

We present mesh puppetry, a variational framework for detail-preserving mesh manipulation through a set of high-level, intuitive, and interactive design tools. Our approach builds upon traditional rigging by optimizing skeleton position and vertex weights in an integrated manner. New poses and animations are created by specifying a few desired constraints on vertex positions, balance of the character, length and rigidity preservation, joint limits, and/or self-collision avoidance. Our algorithm then adjusts the skeleton and solves for the deformed mesh simultaneously through a novel cascading optimization procedure, allowing realtime manipulation of meshes with 50K+ vertices for fast design of pleasing and realistic poses. We demonstrate the potential of our framework through an interactive deformation platform and various applications such as deformation transfer and motion retargeting.

1. Badler, N. I., Manoocherhri, K. H., and Walters, G. 1987. Articulated figure positioning by multiple constraints. IEEE Comput. Graph. Appl. 7, 6, 28–38. Google ScholarDigital Library
2. Baerlocher, P., and Boulic, R. 2004. An inverse kinematic architecture enforcing an arbitrary number of strict priority levels. Visual Computer 20, 6, 402–417. Google ScholarDigital Library
3. Botsch, M., Pauly, M., Gross, M., and Kobbelt, L. 2006. Primo: Coupled prisms for intuitive surface modeling. In Eurographics Symposium on Geometry Processing, 11–20. Google ScholarDigital Library
4. Boulic, R., Mas-Sanso, R., and Thalmann, D. 1997. Complex character positioning based on a compatible flow model of multiple supports. IEEE Transactions on Visualization and Computer Graphics 3, 3, 245–261. Google ScholarDigital Library
5. Chen, Q., and Guan, S.-U. 2004. Incremental multiple objective genetic algorithms. IEEE Trans. on Systems, Man, and Cybernetics 34, 3 (June), 1325–1334. Google ScholarDigital Library
6. ColDet. 2002. Free 3d collision detection library (gnu lgpl). http://sourceforge.net/projects/coldet.Google Scholar
7. Der, K. G., Sumner, R. W., and Popović, J. 2006. Inverse kinematics for reduced deformable models. ACM Trans. Graph. 25, 3, 1174–1179. Google ScholarDigital Library
8. Guskov, I., Sweldens, W., and Schroder, P. 1999. Multiresolution signal processing for meshes. In SIGGRAPH 99 Conference Proceedings, 325–334. Google ScholarDigital Library
9. Huang, J., Shi, X., Liu, X., Zhou, K., Wei, L.-Y., Teng, S.-H., Bao, H., Guo, B., and Shum, H.-Y. 2006. Subspace gradient domain mesh deformation. ACM Trans. Graph. 25, 3, 1126–1134. Google ScholarDigital Library
10. James, D. L., and Twigg, C. D. 2005. Skinning mesh animations. ACM Trans. Graph. 24, 3, 399–407. Google ScholarDigital Library
11. Ju, T., Schaefer, S., and Warren, J. 2005. Mean value coordinates for closed triangular meshes. ACM Trans. Graph. 24, 3, 561–566. Google ScholarDigital Library
12. Kobbelt, L., Campagna, S., Vorsatz, J., and Seidel, H.-P. 1998. Interactive multi-resolution modeling on arbitrary meshes. In SIGGRAPH 98 Conference Proceedings, 105–114. Google ScholarDigital Library
13. Le Callennec, B., and Boulic, R. 2006. Interactive motion deformation with prioritized constraints. Graphical Models 68, 2 (March), 175–193. Google ScholarDigital Library
14. Lewis, J. P., Cordner, M., and Fong, N. 2000. Pose space deformation: a unified approach to shape interpolation and skeleton-driven deformation. In SIGGRAPH 2000 Conference Proceedings, 165–172. Google ScholarDigital Library
15. Lipman, Y., Sorkine, O., Levin, D., and Cohen-Or, D. 2005. Linear rotation-invariant coordinates for meshes. ACM Trans. Graph. 24, 3, 479–487. Google ScholarDigital Library
16. Lipman, Y., Cohen-Or, D., Gal, R., and Levin, D. 2006. Volume and shape preservation via moving frame manipulation. ACM Trans. Graph., to appear. Google ScholarDigital Library
17. Lloyd, S. P. 1982. Least squares quantization in pcm. IEEE Transactions on Information Theory 28, 2, 129 — 137.Google ScholarDigital Library
18. Magnenat-Thalmann, N., Laperrière, R., and Thalmann, D. 1988. Joint-dependent local deformations for hand animation and object grasping. In Proceedings on Graphics interface ’88, 26–33. Google ScholarDigital Library
19. Mohr, A., Tokheim, L., and Gleicher, M. 2003. Direct manipulation of interactive character skins. In Proceedings of the 2003 symposium on Interactive 3D graphics, 27–30. Google ScholarDigital Library
20. Nealen, A., Sorkine, O., Alexa, M., and Cohen-Or, D. 2005. A sketch-based interface for detail-preserving mesh editing. ACM Trans. Graph. 24, 3, 1142–1147. Google ScholarDigital Library
21. Shi, L., Yu, Y., Bell, N., and Feng, W.-W. 2006. A fast multigrid algorithm for mesh deformation. ACM Trans. Graph. 25, 3, 1108–1117. Google ScholarDigital Library
22. Sorkine, O., Cohen-Or, D., Lipman, Y., Alexa, M., Rössl, C., and Seidel, H.-P. 2004. Laplacian surface editing. In Eurographics Symposium on Geometry Processing, 175–184. Google ScholarDigital Library
23. Sumner, R. W., and Popović, J. 2004. Deformation transfer for triangle meshes. ACM Trans. Graph. 23, 3, 399–405. Google ScholarDigital Library
24. Sumner, R. W., Zwicker, M., Gotsman, C., and Popović, J. 2005. Mesh-based inverse kinematics. ACM Trans. Graph. 24, 3, 488–495. Google ScholarDigital Library
25. Teichmann, M., and Teller, S. 1998. Assisted articulation of closed polygonal models. In SIGGRAPH ’98: ACM SIGGRAPH 98 Conference abstracts and applications, 254. Google ScholarDigital Library
26. von Funck, W., Theisel, H., and Seidel, H.-P. 2006. Vector field based shape deformations. ACM Trans. Graph. 25, 3, 1118–1125. Google ScholarDigital Library
27. Yamane, K., and Nakamura, Y. 2003. Natural motion animation through constraining and deconstraining at will. In IEEE Transactions on Visualization and Computer Graphics, no. 3. Google ScholarDigital Library
28. Yu, Y., Zhou, K., Xu, D., Shi, X., Bao, H., Guo, B., and Shum, H.-Y. 2004. Mesh editing with poisson-based gradient field manipulation. ACM Trans. Graph. 23, 3, 644–651. Google ScholarDigital Library
29. Zayer, R., Rössl, C., Karni, Z., and Seidel, H.-P. 2005. Harmonic guidance for surface deformation. In Eurographics 2005, 601–609.Google Scholar
30. Zhao, J., and Badler, N. I. 1994. Inverse kinematics positioning using nonlinear programming for highly articulated figures. ACM Trans. Graph. 13, 4, 313–336. Google ScholarDigital Library
31. Zhou, K., Huang, J., Snyder, J., Liu, X., Bao, H., Guo, B., and Shum, H.-Y. 2005. Large mesh deformation using the volumetric graph laplacian. ACM Trans. Graph. 24, 3, 496–503. Google ScholarDigital Library
32. Zorin, D., Schröderr, P., and Sweldens, W. 1997. Interactive multiresolution mesh editing. In SIGGRAPH 97 Conference Proceedings, 259–268. Google ScholarDigital Library