“Measuring and modeling the appearance of finished wood” by Marschner, Westin, Arbree and Moon

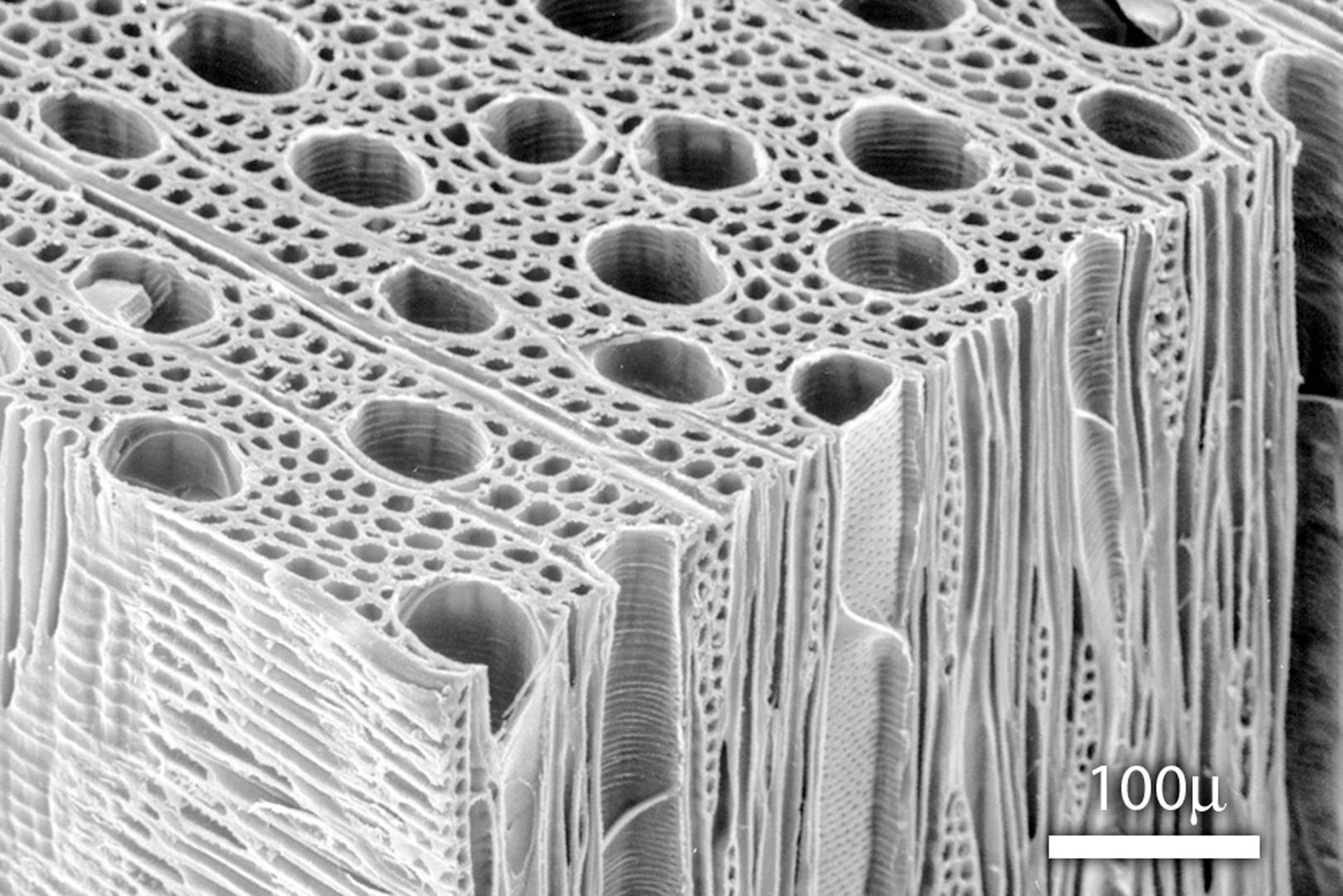
Wood coated with transparent finish has a beautiful and distinctive appearance that is familiar to everyone. Woods with unusual grain patterns. such as tiger, burl, and birdseye figures, have a strikingly unusual directional reflectance that is prized for decorative applications. With new, high resolution measurements of spatially varying BRDFs. we show that this distinctive appearance is due to light scattering that does not conform to the usual notion of anisotropic surface reflection. The behavior can be explained by scattering from the matrix of wood fibers below the surface, resulting in a subsurface highlight that occurs on a cone with an out-of-plane axis. We propose a new shading model component to handle reflection from subsurface fibers, which is combined with the standard diffuse and specular components to make a complete shading model. Rendered results from fits of our model to the measurement data demonstrate that this new model captures the distinctive appearance of wood.

1. Ashikhmin, M., and Shirley, P. S. 2000. An anisotropic phong brdf model. Journal of Graphics Tools 5, 2, 25–32. Google ScholarDigital Library
2. Dana, K. J., Van Ginneken, B., Nayar, S. K., and Koenderink, J. J. 1999. Reflectance and texture of real-world surfaces. ACM Transactions on Graphics 18, 1, 1–34. Google ScholarDigital Library
3. Gardner, A., Tchou, C., Hawkins, T., and Debevec, P. 2003. Linear light source reflectometry. ACM Transactions on Graphics 22, 3 (July), 749–758. Google ScholarDigital Library
4. Hanrahan, P., and Krueger, W. 1993. Reflection from layered surfaces due to subsurface scattering. In Proc. SIGGRAPH 93, 165–174. Google ScholarDigital Library
5. Harris, J. M. 1989. Spiral Grain and Wave Phenomena in Wood Formation. Springer-Verlag, Berlin.Google Scholar
6. He, X. D., Torrance, K. E., Sillion, F. X., and Greenberg, D. P. 1991. A comprehensive physical model for light reflection. Computer Graphics (Proc. SIGGRAPH) 25, 4, 175–186. Google ScholarDigital Library
7. Jensen, H. W., Marschner, S. R., Levoy, M., and Hanrahan, P. 2001. A practical model for subsurface light transport. In Proc. SIGGRAPH 2001, 511–518. Google ScholarDigital Library
8. Kajiya, J. T., and Kay. T. L. 1989. Rendering fur with 3D textures. In Proceedings of SIGGRAPH 1989, 271–280. Google ScholarDigital Library
9. Kajiya, J. T. 1985. Anisotropic reflection models. Computer Graphics (Proc. SIGGRAPH) 19, 3, 15–21. Google ScholarDigital Library
10. Lefebvre, L., and Poulin, P. 2000. Analysis and synthesis of structural textures. In Graphics Interface, 77–86.Google Scholar
11. Levoy, M., 2004. The Stanford Spherical Gantry. http://graphics.stanford.edu/projects/gantry.Google Scholar
12. Lewin, M., and Goldstein, I. S., Eds. 1991. Wood Structure and Composition. Dekker. New York.Google Scholar
13. Lewis, J.-P. 1989. Algorithms for solid noise synthesis. In Proc. SIGGRAPH 89, 263–270. Google ScholarDigital Library
14. Lu, R., Koenderink, J. J., and Kappers, A. M. L. 2000. Specularities on surfaces with tangential hairs or grooves. Computer Vision and Image Understanding 78, 320–335. Google ScholarDigital Library
15. Marschner, S. R., Jensen, H. W., Cammarano, M., Worley, S., and Hanrahan, P. 2003. Light scattering from human hair fibers. ACM Transactions on Graphics (Proc. SIGGRAPH) 22, 3, 780–791. Google ScholarDigital Library
16. Mcallister, D. K. 2002. A Generalized Surface Appearance Representation for Computer Graphics. PhD thesis, University of North Carolina at Chapel Hill. Google ScholarDigital Library
17. Nyström, J. 2003. Automatic measurement of fiber orientation in softwoods by using the tracheid effect. Computers and Electronics in Agriculture 41, 1–3 (Dec.), 91–99.Google ScholarCross Ref
18. Peachey, D. R. 1985. Solid texturing of complex surfaces. In Proc. SIGGRAPH 85, 279–286. Google ScholarDigital Library
19. Pont, S. C., and Koenderink, J. J. 2003. Split off-specular reflection and surface scattering from woven materials. Applied Optics 42, 1526–1533.Google ScholarCross Ref
20. Poulin, P., and Fournier, A. 1990. A model for anisotropic reflection. Computer Graphics (Proc. SIGGRAPH) 24, 4, 273–282. Google ScholarDigital Library
21. Saarinen, K., and Muinonen, K. 2001. Light scattering by wood fibers. Applied Optics 40, 28 (Oct.), 5064–5077.Google ScholarCross Ref
22. Shirley, P., and Chiu, K. 1997. A low distortion map between disk and square. Journal of Graphics Tools 2, 3, 45–52. Google ScholarDigital Library
23. Stam, J. 1995. Multiple scattering as a diffusion process. In Eurographics Rendering Workshop 1995, 41–50.Google ScholarCross Ref
24. Ward, G. J. 1992. Measuring and modeling anisotropic reflection. Computer Graphics (Proc. SIGGRAPH) 26, 2, 265–272. Google ScholarDigital Library
25. Wilson, K., and White, D. J. B. 1986. The Anatomy of Wood: Its diversity and variability. Stobart and Son, London.Google Scholar
26. Wolff, L. B., Nayar, S. K., and Oren, M. 1998. Improved diffuse reflection models for computer vision. International Journal of Computer Vision 30, 1, 55–71. Google ScholarDigital Library