“LOD +: augmenting LOD with skeletons” by Benoit and Rodriguez
Conference:
Type(s):
Entry Number: 70
Title:
- LOD +: augmenting LOD with skeletons
Presenter(s)/Author(s):
Abstract:
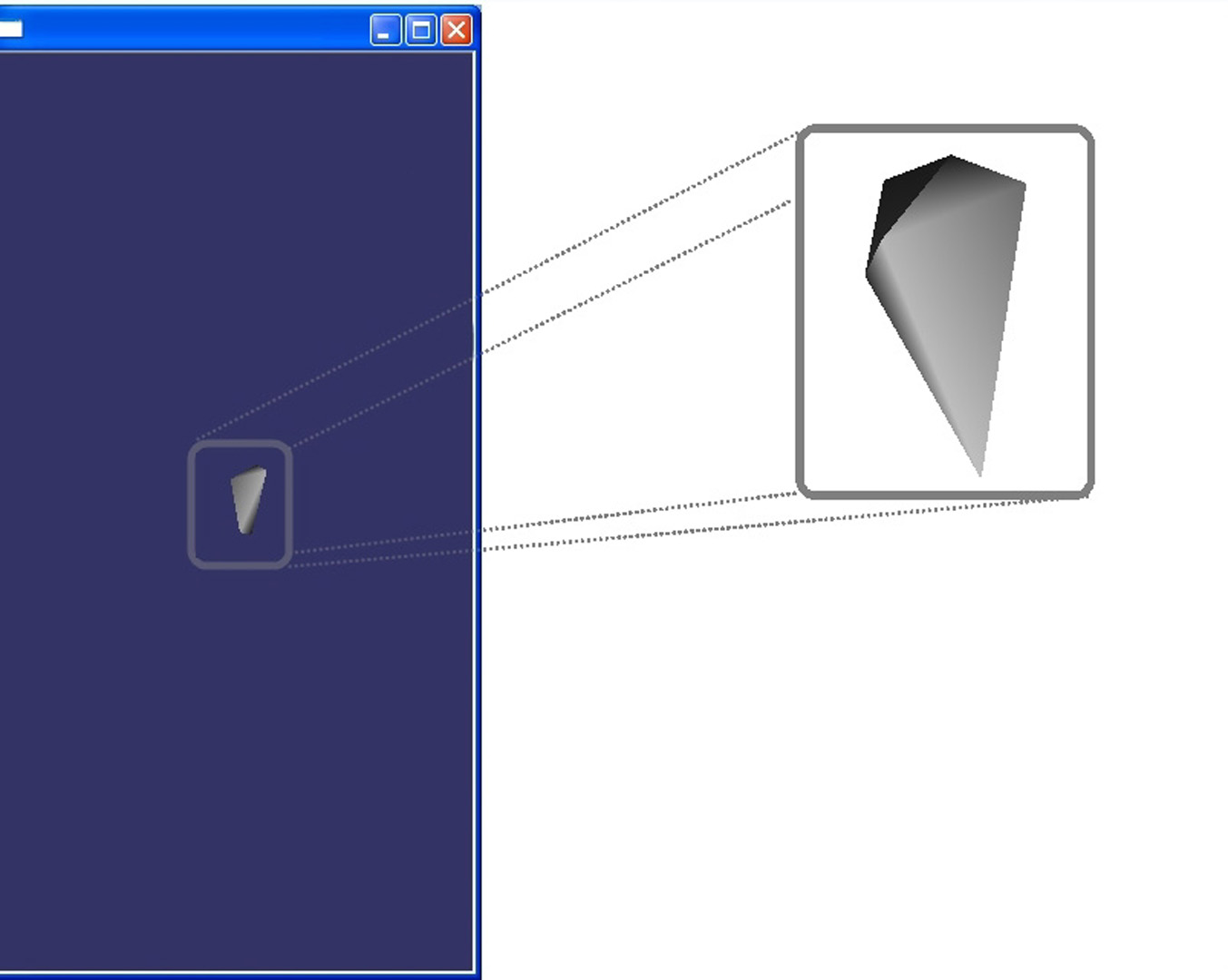
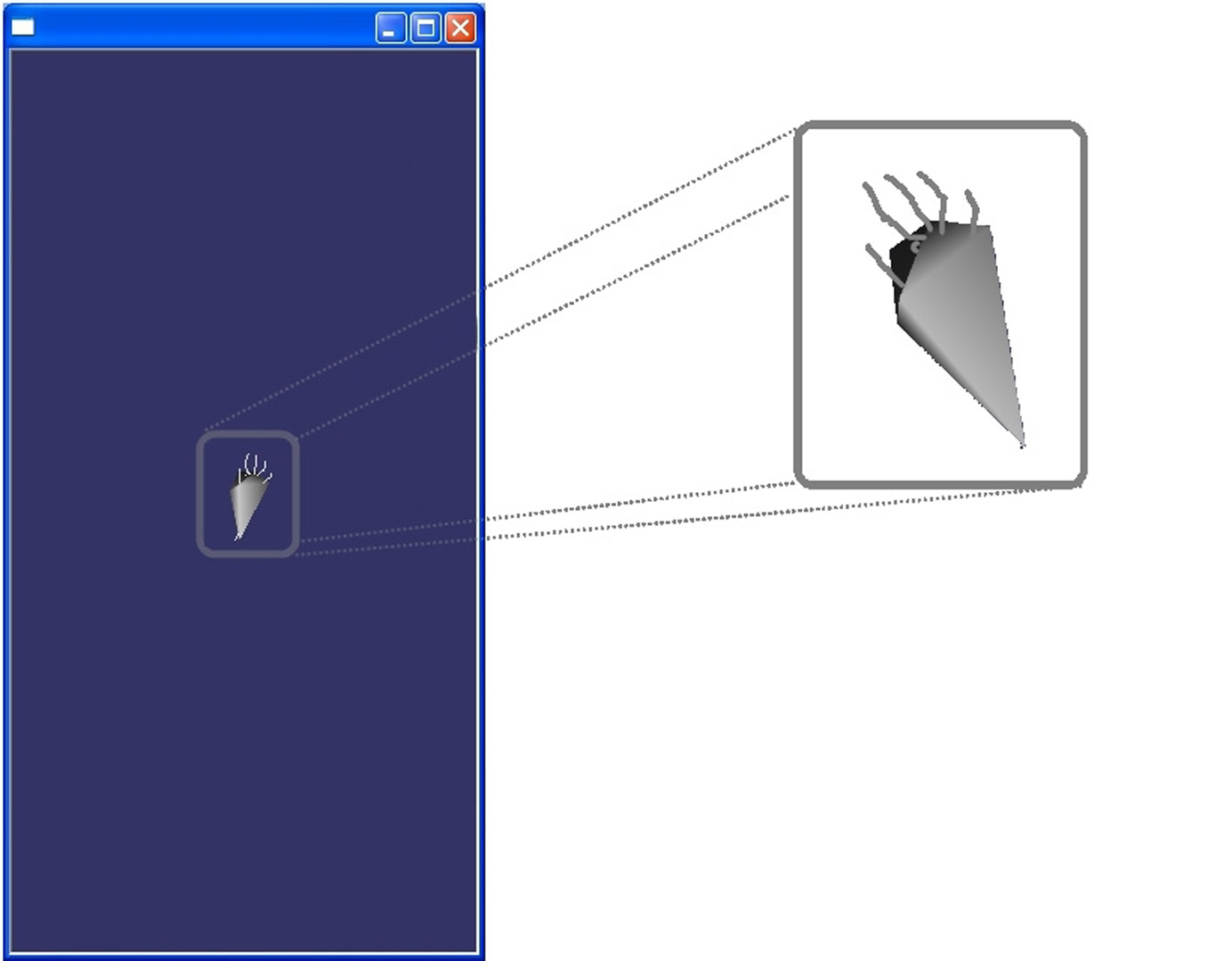
Until now computer graphic researchers have tried to solve visualization problems introduced by the size of meshes. Modern tools produce large models and hardware is not able to render them in full resolution. For example, the digital Michelangelo project extracted a model with more than one billion polygons. One can notice hardware has become more and more powerful but meshes have also become more and more complex. To solve this issue, people have worked on many solutions. We can find solutions based on space subdivision, or based on visibility of objects like the use of a Z-buffer. But in 1976, Clark [Clark 1976] introduces the level of detail concept (LOD). The principle of LOD is the construction of several versions of the same 3D model at different resolutions. This is achieved by removing some object features. Luebke provides in [Luebke 1997] a very complete survey of LOD algorithms. The main issue with the simplification is that the mesh does not preserve appearance of the original mesh. Indeed, important features tend to disappear. For example, with the Quadric Error Metrics (QEM) algorithms and the cow mesh, the tail, horn and other characteristic points merge with the mesh at a low resolution. Our approach allows the simplified mesh to preserve important details.
References:
Clark, J. H. 1976. Hierarchical geometric models for visible surface algorithms. Commun. ACM 19, 10, 547–554. Google ScholarDigital Library
Garland, M., and Heckbert, P. S. 1997. Surface simplification using quadric error metrics. In SIGGRAPH ’97: Proceedings of the 24th annual conference on Computer graphics and interactive techniques, ACM Press/Addison-Wesley Publishing Co., New York, NY, USA, 209–216. Google ScholarDigital Library
Luebke, D. 1997. A survey of polygonal simplification algorithms.Google Scholar
Reeb, G. 1946. Sur les points singuliers d’une forme de complment intgrable ou d’une fonction numrique. Comptes Rendus de L’Acadmie des Sances 222, 847–849.Google Scholar
Tierny, J., Vandeborre, J.-P., and Daoudi, M. 2006. 3d Mesh Skeleton Extraction Using Topological and Geometrical Analyses. In 14th Pacific Conference on Computer Graphics and Applications (Pacific Graphics 2006), 85–94.Google Scholar
Additional Images: