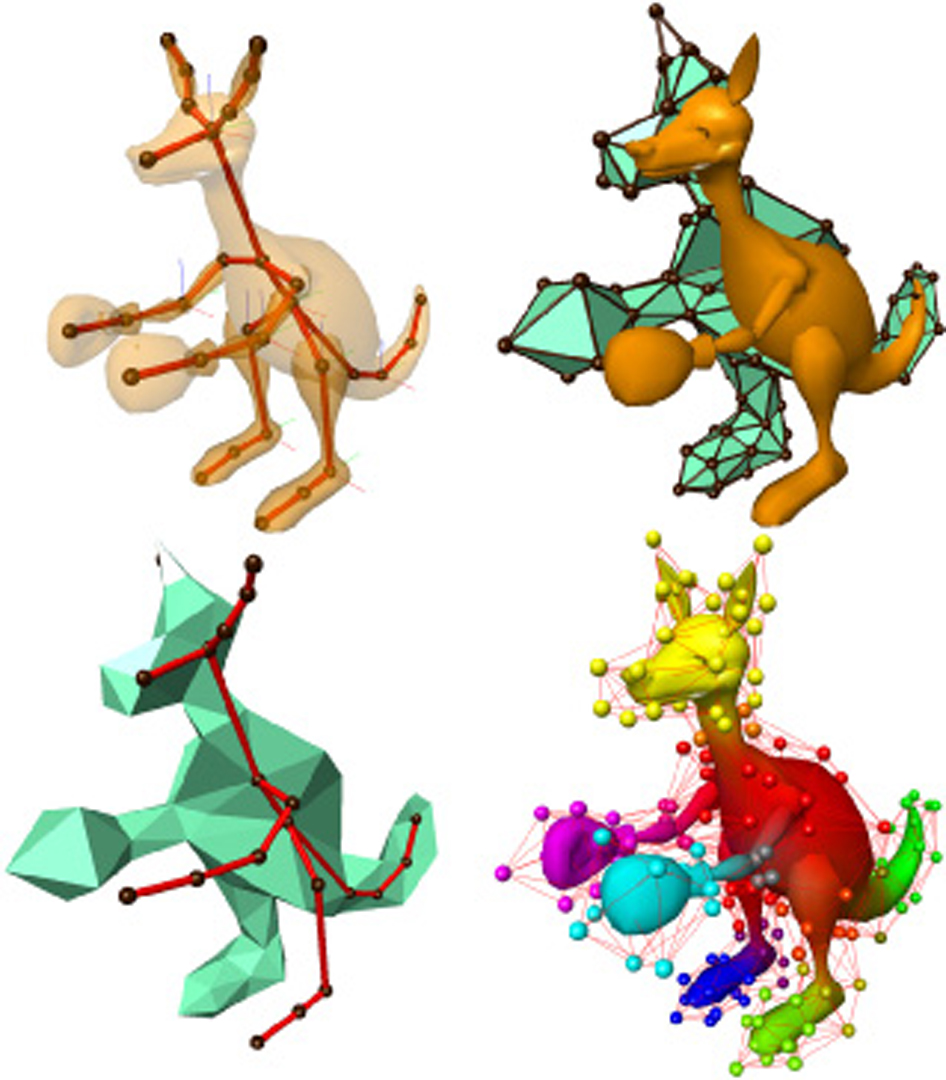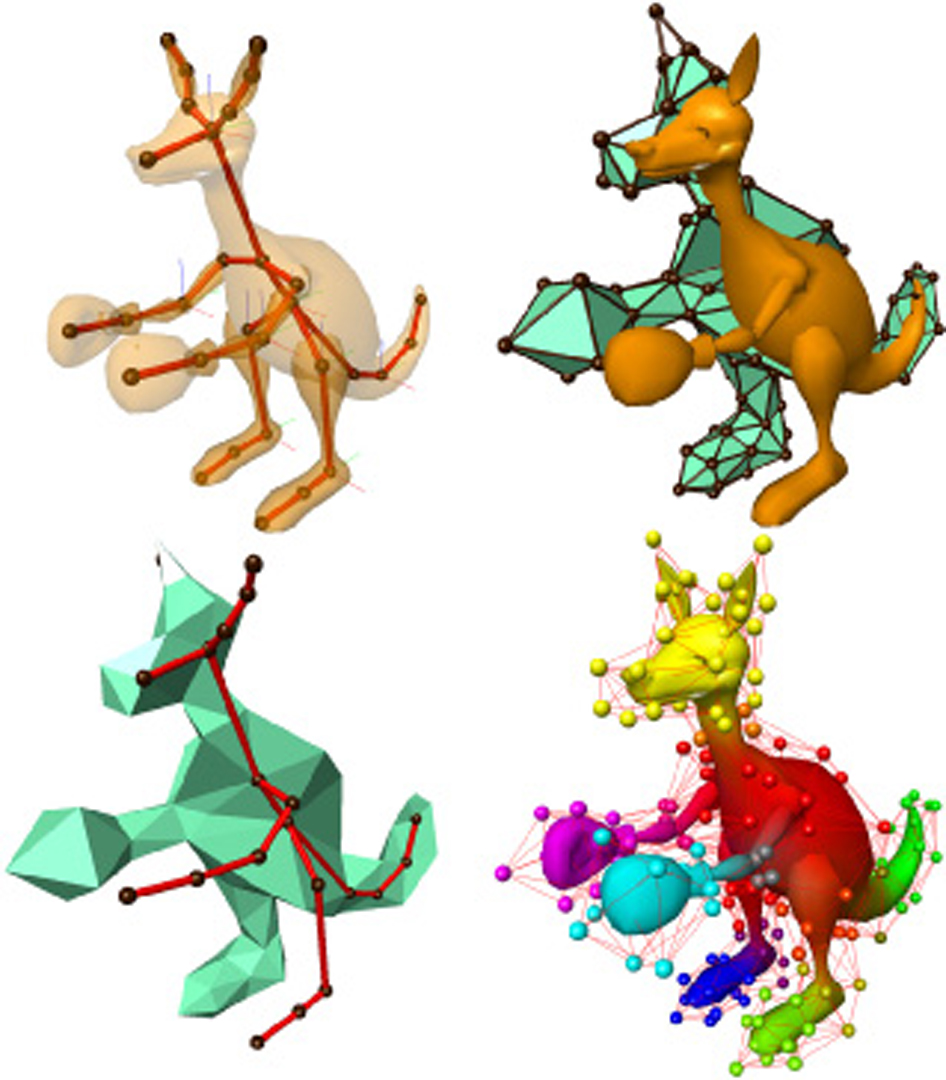“Interactive skeleton-driven dynamic deformations” by Capell, Green, Curless, Duchamp and Popovic
Conference:
Type(s):
Title:
- Interactive skeleton-driven dynamic deformations
Presenter(s)/Author(s):
Abstract:
This paper presents a framework for the skeleton-driven animation of elastically deformable characters. A character is embedded in a coarse volumetric control lattice, which provides the structure needed to apply the finite element method. To incorporate skeletal controls, we introduce line constraints along the bones of simple skeletons. The bones are made to coincide with edges of the control lattice, which enables us to apply the constraints efficiently using algebraic methods. To accelerate computation, we associate regions of the volumetric mesh with particular bones and perform locally linearized simulations, which are blended at each time step. We define a hierarchical basis on the control lattice, so for detailed interactions the simulation can adapt the level of detail. We demonstrate the ability to animate complex models using simple skeletons and coarse volumetric meshes in a manner that simulates secondary motions at interactive rates.
References:
1. AUBEL, A., AND THALMANN, D. 2000. Realistic deformation of human body shapes. In Proceedings of Computer Animation and Simulation 2000, 125-135.Google Scholar
2. BANK, R. E. 1996. Hierarchical bases and the finite element method, vol. 5 of Acta Numerica. Cambridge University Press, Cambridge, 1-43.Google Scholar
3. BARAFF, D., AND WITKIN, A. 1992. Dynamic simulation of non-penetrating flexible bodies. Computer Graphics (Proceedings of SIGGRAPH 92) 26, 2, 303-308. Google Scholar
4. BARAFF, D., AND WITKIN, A. 1998. Large steps in cloth simulation. In Proceedings of SIGGRAPH 98, 43-54. Google Scholar
5. BRO-NIELSEN, M., AND COTIN, S. 1996. Real-time volumetric deformable models for surgery simulation using finite elements and condensation. Computer Graphics Forum (Proceedings of Eurographics ’96) 15, 3, 57-66. Google Scholar
6. CAPELL, S., GREEN, S., CURLESS, B., DUCHAMP, T., AND POPOVIĆ, Z. 2002. A multiresolution framework for dynamic deformations. University of Washington, Department of Computer Science and Engineering, Technical Report 02-04-02.Google Scholar
7. CIRAK, F., AND ORTIZ, M. 2001. Fully c1-conforming subdivision elements for finite deformation thin-shell analysis. International Journal for Numerical Methods in Engineering 51, 7 (July), 813-833.Google Scholar
8. DEBUNNE, G., DESBRUN, M., BARR, A., AND CANI, M.-P. 1999. Interactive multiresolution animation of deformable models. Eurographics Workshop on Animation and Simulation.Google Scholar
9. DEBUNNE, G., DESBRUN, M., CANI, M.-P., AND BARR, A. H. 2001. Dynamic real-time deformations using space & time adaptive sampling. In Proceedings of SIGGRAPH 2001, 31-36. Google Scholar
10. DESBRUN, M., SCHRÖDER, P., AND BARR, A. 1999. Interactive animation of structured deformable objects. Graphics Interface ’99 (June), 1-8. Google Scholar
11. FALOUTSOS, P., VAN DE PANNE, M., AND TERZOPOULOS, D. 1997. Dynamic free-form deformations for animation synthesis. IEEE Transactions on Visualization and Computer Graphics 3, 3 (July-Sept.), 201-214. Google Scholar
12. GORTLER, S. J., AND COHEN, M. F. 1995. Hierarchical and variational geometric modeling with wavelets. Symposium on Interactive 3D Graphics, 35-42. Google Scholar
13. GOURRET, J.-P., THALMANN, N. M., AND THALMANN, D. 1989. Simulation of object and human skin deformations in a grasping task. Computer Graphics (Proceedings of SIGGRAPH 89) 23, 3 (July), 21-30. Google Scholar
14. GRINSPUN, E., KRYSL, P., AND SCHRÖDER, P. 2002. Charms: A simple framework for adaptive simulation. To appear in the Proceedings of SIGGRAPH 2002. Google Scholar
15. HSU, W. M., HUGHES, J. F., AND KAUFMAN, H. 1992. Direct manipulation of free-form deformations. Computer Graphics (Proceedings of SIGGRAPH 92) 26, 2 (July), 177-184. Google Scholar
16. JAMES, D. L., AND PAI, D. K. 1999. Artdefo – accurate real time deformable objects. Proceedings of SIGGRAPH 99 (August), 65-72. Google Scholar
17. KOCH, R. M., GROSS, M. H., CARLS, F. R., VON BÜREN, D. F., FANKHAUSER, G., AND PARISH, Y. 1996. Simulating facial surgery using finite element methods. Proceedings of SIGGRAPH 96 (August), 421-428. Google Scholar
18. LEWIS, J. P., CORDNER, M., AND FONG, N. 2000. Pose space deformation: A unified approach to shape interpolation and skeleton-driven deformation. In Proceedings of SIGGRAPH 2000, 165-172. Google Scholar
19. LI, X., WOON, T. W., TAN, T. S., AND HUANG, Z. 2001. Decomposing polygon meshes for interactive applications. In ACM Symposium on Interactive 3D Graphics, 35-42. Google Scholar
20. MACCRACKEN, R., AND JOY, K. I. 1996. Free-form deformations with lattices of arbitrary topology. Computer Graphics (Proceedings of SIGGRAPH 96) 30, 181-188. Google Scholar
21. METAXAS, D., AND TERZOPOULOS, D. 1992. Dynamic deformation of solid primitives with constraints. Computer Graphics (Proceedings of SIGGRAPH 92) 26, 2 (July), 309-312. Google Scholar
22. PENTLAND, A., AND WILLIAMS, J. 1989. Good vibrations: Modal dynamics for graphics and animation. Computer Graphics (Proceedings of SIGGRAPH 89) 23, 3 (July), 215-222. Google Scholar
23. PICINBONO, G., DELINGETTE, H., AND AYACHE, N. 2000. Real-time large displacement elasticity for surgery simulation: Non-linear tensor-mass model. In Proceedings of the Third International Conference on Medical Robotics, Imaging and Computer Assisted Surgery: MICCAI 2000, 643-652. Google Scholar
24. PLATT, J. C., AND BARR, A. H. 1988. Constraint methods for flexible models. Computer Graphics (Proceedings of SIGGRAPH 88) 22, 4 (August), 279-288. Google Scholar
25. PRENTER, P. M. 1975. Splines and Variational Methods. John Wiley and Sons.Google Scholar
26. ROTH, S. H. M., GROSS, M. H., TURELLO, S., AND CARLS, F. R. 1998. A bernstein-bézier based approach to soft tissue simulation. Computer Graphics Forum 17, 3, 285-294.Google Scholar
27. SEDERBERG, T. W., AND PARRY, S. R. 1986. Free-form deformation of solid geometric models. Computer Graphics (Proceedings of SIGGRAPH 86) 20, 4 (Aug.), 151-160. Google Scholar
28. SHABANA, A. 1998. Dynamics of Multibody Systems. Cambridge University Press.Google Scholar
29. SINGH, K., AND KOKKEVIS, E. 2000. Skinning characters using Surface-Oriented Free-Form deformations. In Proceedings of the Graphics Interface 2000, 35-42.Google Scholar
30. SLOAN, P.-P. J., ROSE, C. F., AND COHEN, M. F. 2001. Shape by example. In Symposium on Interactive 3D Graphics, 135-144. Google Scholar
31. STOLLNITZ, E. J., DEROSE, T. D., AND SALESIN, D. H. 1996. Wavelets for Computer Graphics: Theory and Applications. Morgan Kaufmann, San Francisco, CA. Google Scholar
32. TEICHMANN, M., AND TELLER, S. 1998. Assisted articulation of closed polygonal models. In Computer Animation and Simulation ’98, 87-101. Google Scholar
33. TERZOPOULOS, D., AND FLEISCHER, K. 1988. Modeling Inelastic deformation: Viscoelasticity, plasticity, fracture. Computer Graphics (Proceedings of SIGGRAPH 88) 22, 4 (August), 269-278. Google Scholar
34. TERZOPOULOS, D., AND WITKIN, A. 1988. Physically based models with rigid and deformable components. IEEE Computer Graphics and Applications 8, 6 (Nov.), 41-51. Google Scholar
35. TERZOPOULOS, D., PLATT, J., BARR, A., AND FLEISCHER, K. 1987. Elastically deformable models. Computer Graphics (Proceedings of SIGGRAPH 87) 21, 4 (July), 205-214. Google Scholar
36. WILHELMS, J., AND GELDER, A. V. 1997. Anatomically based modeling. In Proceedings of SIGGRAPH 97, 173-180. Google Scholar
37. WITKIN, A., AND WELCH, W. 1990. Fast animation and control of nonrigid structures. Computer Graphics (Proceedings of SIGGRAPH 90) 24, 4 (August), 243-252. Google Scholar