“Interactive multiresolution surface viewing” by Certain, Popović, DeRose, Duchamp, Salesin, et al. …
Conference:
Type(s):
Title:
- Interactive multiresolution surface viewing
Presenter(s)/Author(s):
Abstract:
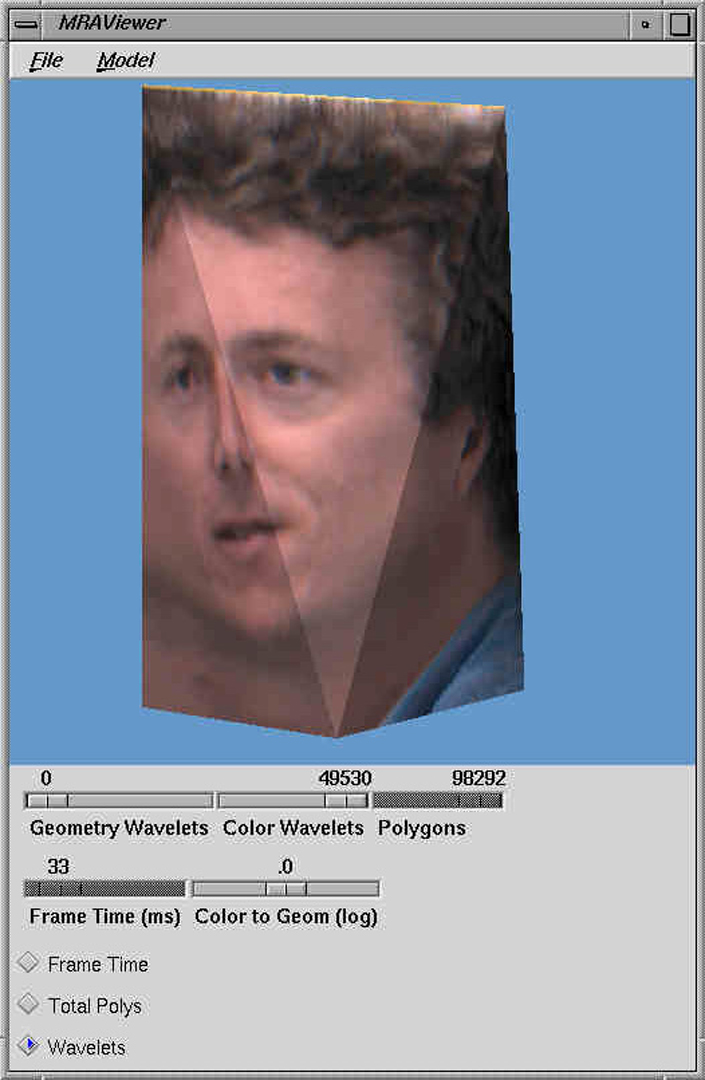
Multiresolution analysis has been proposed as a basic tool supporting compression, progressive transmission, and level-of-detail control of complex meshes in a unified and theoretically sound way. We extend previous work on multiresolution analysis of meshes in two ways. First, we show how to perform multiresolution analysis of colored meshes by separately analyzing shape and color. Second, we describe efficient algorithms and data structures that allow us to incrementally construct lower resolution approximations to colored meshes from the geometry and color wavelet coefficients at interactive rates. We have integrated these algorithms in a prototype mesh viewer that supports progressive transmission, dynamic display at a constant frame rate independent of machine characteristics and load, and interactive choice of tradeoff between the amount of detail in geometry and color. The viewer operates as a helper application to Netscape, and can therefore be used to rapidly browse and display complex geometric models stored on the World Wide Web.
References:
1. Matthias Eck, Tony DeRose, Tom Duchamp, Hugues Hoppe, Michael Lounsbery, and Werner Stuetzle. Multiresolution analysis of arbitrary meshes. In Robert Cook, editor, SIGGRAPH 95 Conference Proceedings, Annual Conference Series, pages 173-182. ACM SIGGRAPH, Addison Wesley, August 1995. held in Los Angeles, California, 06-11 August 1995.
2. Adam Finkelstein and David Salesin. Multiresolution curves. Computer Graphics (SIGGRAPH ’94 Proceedings), 28(3):261-268, July 1994.
3. H. Hoppe. Progressive meshes. In SIGGRAPH 96 Conference Proceedings, Annual Conference Series. ACM SIGGRAPH, Addison Wesley, August 1996. held in New Orleans, Louisiana, 04-09 August 1996.
4. H. Hoppe, T. DeRose, T. Duchamp, J. McDonald, and W. Stuetzle. Mesh optimization. In J.T. Kajiya, editor, SIGGRAPH 93 Conference Proceedings, Annual Conference Series, pages 19-26. ACM SIG- GRAPH, Addison Wesley, August 1993. held in Anaheim, California, 01-06 August 1993.
5. J. Michael Lounsbery. Multiresolution Analysis for Surfaces of Arbitrary Topological Type. PhD thesis, Department of Computer Science and Engineering, University of Washington, September 1994. Available as ftp://cs.washington.edu/pub/graphics/LounsPhd.ps.Z.
6. Michael Lounsbery, Tony DeRose, and Joe Warren. Multiresolution analysis for surfaces of arbitrary topological type. Submitted for publication, 1994. Preliminary version available as Technical Report 93-10-05b, Department of Computer Science and Engineering, University of Washington, January, 1994. Also available as ftp://cs.washington.edu/pub/graphics/TR931005b.ps.Z.
7. Stephane Mallat. A theory for multiresolution signal decomposition: The wavelet representation. IEEE Transactions on Pattern Analysis and Machine Intelligence, 11(7):674-693, July 1989.
8. Yves Meyer. Ondelettes et fonctions splines. Technical report, S~minaire EDP, l~cole Polytechnique, Paris, 1986.
9. J. Rossignac and E Borrel. Multi-resolution 3D approximations for rendering. In B. Falcidieno and T.L. Kunii, editors,Modeling in Computer Graphics, pages 455-465. Springer-Verlag, June-July 1993.
10. Peter Schr6der and Wim Sweldens. Spherical wavelets: Efficiently representing functions on the sphere. In Robert Cook, editor, SIG- GRAPH 95 Conference Proceedings, Annual Conference Series, pages 161-172. ACM SIGGRAPH, Addison Wesley, August 1995. held in Los Angeles, California, 06-11 August 1995.
11. Eric Stollnitz, Tony DeRose, and David Salesin. Wavelets for Computer Graphics: Theory and Applications~ Morgan-Kaufmann, 1996.