“Interactive geometry remeshing”

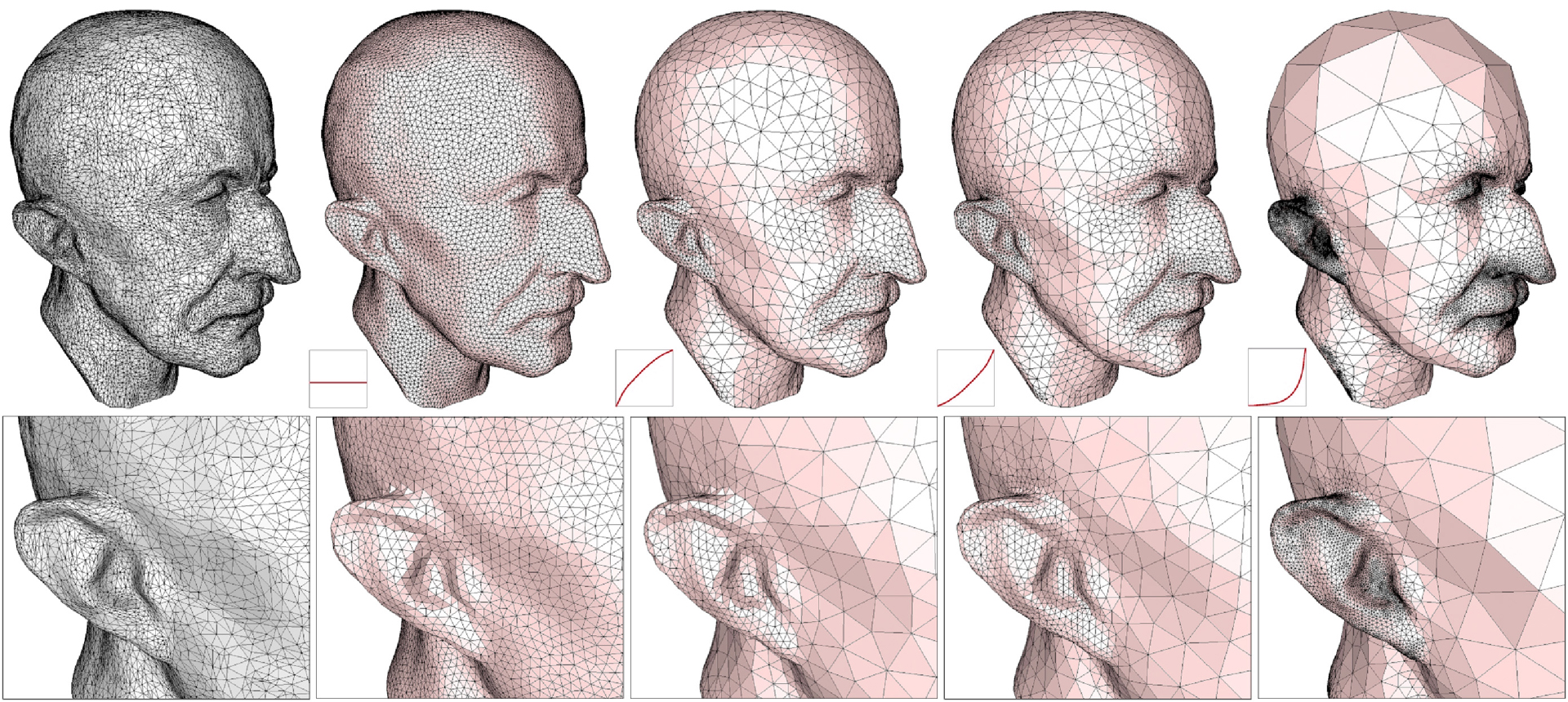
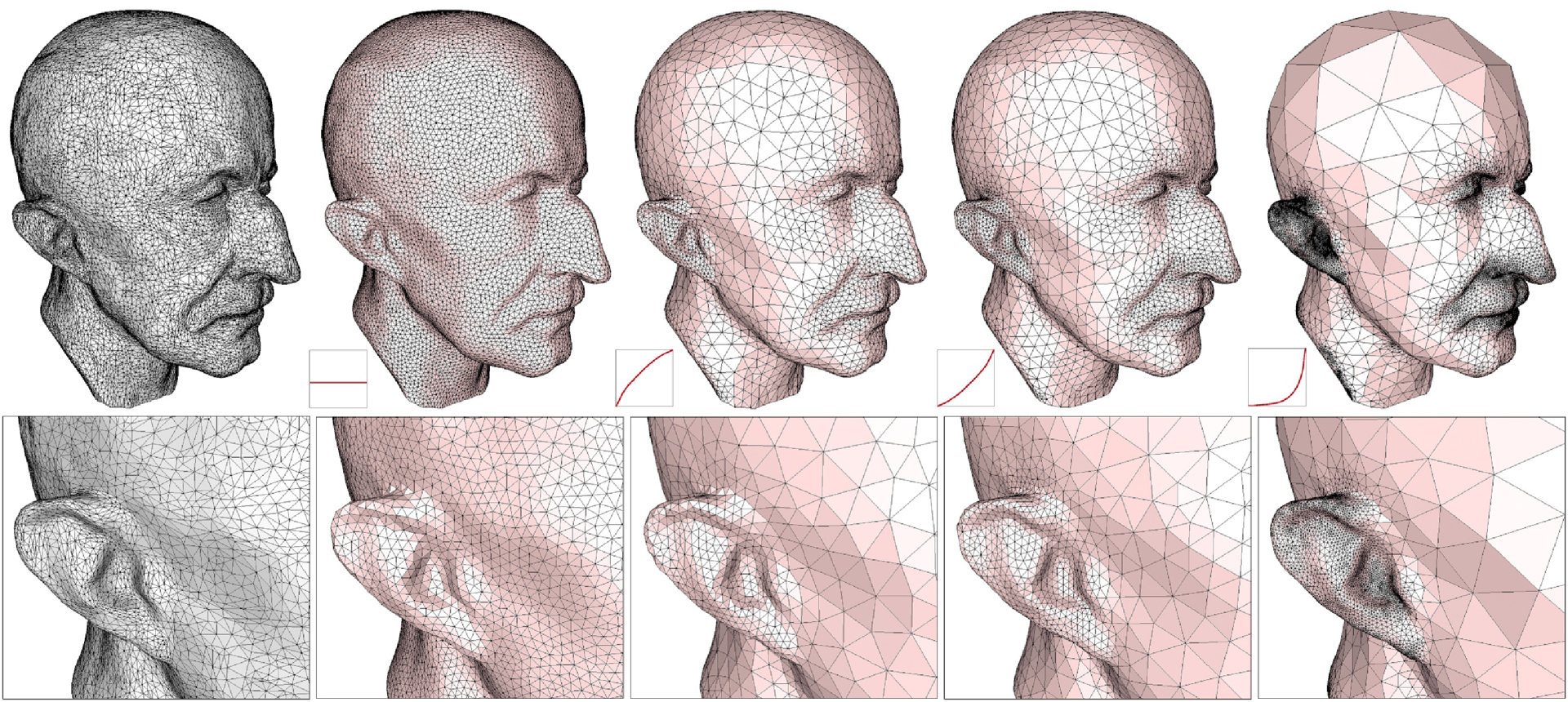
We present a novel technique, both flexible and efficient, for interactive remeshing of irregular geometry. First, the original (arbitrary genus) mesh is substituted by a series of 2D maps in parameter space. Using these maps, our algorithm is then able to take advantage of established signal processing and halftoning tools that offer real-time interaction and intricate control. The user can easily combine these maps to create a control map — a map which controls the sampling density over the surface patch. This map is then sampled at interactive rates allowing the user to easily design a tailored resampling. Once this sampling is complete, a Delaunay triangulation and fast optimization are performed to perfect the final mesh.As a result, our remeshing technique is extremely versatile and general, being able to produce arbitrarily complex meshes with a variety of properties including: uniformity, regularity, semi-regularity, curvature sensitive resampling, and feature preservation. We provide a high level of control over the sampling distribution allowing the user to interactively custom design the mesh based on their requirements thereby increasing their productivity in creating a wide variety of meshes.

1. www.cgal.org: Computational Geometry Algorithms Library.Google Scholar
2. BOROUCHAKI, H. Geometric Surface Mesh. In 2nd International Conference on Integrated and Manufacturing in Mechanical Engineering (may 1998), pp.343-350.Google Scholar
3. BOROUCHAKI, H., GEORGE, P. L., HECHT, F., LAUG, P., AND SALTEL, E. Delaunay Mesh Generation Governed by Metric Specifications. Finite Elements in Analysis and Design 25 (1997), pp.61-83. Google Scholar
4. BOROUCHAKI, H., HECHT, F., AND FREY, P. J. Mesh Gradation Control. In Proceedings of 6th International Meshing Roundtable, Sandia National Labs (oct 1997), pp. 131-141.Google Scholar
5. BOSSEN, F., AND HECKBERT, P. A Pliant Method for Anisotropic Mesh Generation. In 5th Intl. Meshing Roundtable (oct 1996), pp.63-76.Google Scholar
6. BOTSCH, M., AND KOBBELT, L. Resampling Feature and Blend Regions in Polygonal Meshes for Surface Anti-Aliasing. In Eurographics proceedings (sep 2001), pp.402-410.Google Scholar
7. BOTSCH, M., RÖSSL, C., AND KOBBELT, L. Feature Sensitive Sampling for Interactive Remeshing. In Vision, Modeling and Visualization proceedings (2000), pp. 129-136.Google Scholar
8. DE COUGNY, H. L., AND SHEPHARD, M. S. Surface Meshing Using Vertex Insertion. In Proceedings of 5th International Meshing Roundtable, Sandia National Labs (oct 1996), pp.243-256.Google Scholar
9. DESBRUN, M., MEYER, M., AND ALLIEZ, P. Intrinsic parameterizations of surface meshes. In Proceedings of Eurographics (2002).Google Scholar
10. DYN, N., HORMANN, K., S.-J. KIM, AND LEVIN, D. Optimizing 3D Triangulations using Discrete Curvature Analysis. Mathematical methods for curves and surfaces, Oslo 2000 (2001), pp. 135-146. Google Scholar
11. ECK, M., DEROSE, T., DUCHAMP, T., HOPPE, H., LOUNSBERY, M., AND STUETZLE, W. Multiresolution Analysis of Arbitrary Meshes. In Proceedings of SIGGRAPH (1995), pp. 173-182. Google Scholar
12. ERIKSON, J., AND HAR-PELED, S. Optimally cutting a surface into a disk. In Proceedings of the 18th Annual ACM Symposium on Computational Geometry (2002). to appear. Google Scholar
13. FREY, P. J. About Surface Remeshing. In Proceedings of the 9th Int. Meshing Roundtable (2000), pp. 123-136.Google Scholar
14. GARLAND, M., AND HECKBERT, P. Simplifying Surfaces with Color and Texture using Quadric Error Metrics. In IEEE Visualization Conference Proceedings (1998), pp.263-269. Google Scholar
15. GARLAND, M., WILLMOTT, A., AND HECKBERT, P. Hierarchical Face Clustering on Polygonal Surfaces. In ACM Symposium on Interactive 3D Graphics (2001). Google Scholar
16. GEORGE, P. L., AND BOROUCHAKI, H., Eds. Delaunay Triangulation and Meshing Application to Finite Elements. HERMES, Paris, 1998.Google Scholar
17. GRAY, A., Ed. Modern Differential Geometry of Curves and Surfaces. Second edition. CRC Press, 1998. Google Scholar
18. GRIMM, C. M., AND HUGHES, J. F. Modeling Surfaces of Arbitrary Topology using Manifolds. In Proceedings of SIGGRAPH (1995), pp.359-368. Google Scholar
19. GU, X., GORTLER, S., AND HOPPE, H. Geometry Images. In Proceedings of SIGGRAPH (2002). Google Scholar
20. GUSKOV, I., SWELDENS, W., AND SCHRÖDER, P. Multiresolution Signal Processing for Meshes. In Proceedings of SIGGRAPH (1999), pp. 325-334. Google Scholar
21. GUSKOV, I., VIDIMCE, K., SWELDENS, W., ANDSCHRÖDER, P. Normal Meshes. In Proceedings of SIGGRAPH (2000), pp.95-102. Google Scholar
22. HORMANN, K., LABSIK, U., AND GREINER, G. Remeshing Triangulated Surfaces with Optimal Parameterizations. Computer-Aided Design 33 (2001), pp.779-788.Google Scholar
23. LAZARUS, F., POCCHIOLA, M., VEGTER, G., AND VERROUST, A. Computing a Canonical Polygonal Schema of an Orientable Triangulated Surface. In Proceedings of 17th Annu. ACM Sympos. Comput. Geom. (2001), pp.80-89. Google Scholar
24. LEE, A. W. F., SWELDENS, W., SCHRÖDER, P., COWSAR, L., AND DOBKIN, D. MAPS: Multiresolution Adaptive Parameterization of Surfaces. In Proceedings of SIGGRAPH (1998), pp.95-104. Google Scholar
25. LÉVY, B. Constrained Texture Mapping for Polygonal Meshes. In Proceedings of SIGGRAPH (2001), pp.417-424. Google Scholar
26. LÉVY, B., PETITJEAN, S., RAY, N., AND MAILLOT, J. Least Squares Conformal Maps for Automatic Texture Atlas Generation. In Proceedings of SIGGRAPH (2002). Google Scholar
27. LINDSTROM, P., AND TURK, G. Fast and Memory Efficient Polygonal Simplification. In IEEE Visualization Proceedings (1998), pp. 279-286. Google Scholar
28. MEYER, M., DESBRUN, M., SCHRÖDER, P., AND BARR, A. H. Discrete Differential-Geometry Operators for Triangulated 2-Manifolds, 2002. http://multires.caltech.edu/pubs/diffGeoOps.pdf. Google Scholar
29. OSTROMOUKHOV, V. A Simple and Efficient Error-Diffusion Algorithm. In Proceedings of SIGGRAPH (2001), pp.567-572. Google Scholar
30. P. VÉRON, J.-C. L. Static Polyhedron Simplification using Error Measurements. Computer-Aided Design 29(4) (1997), pp.287-298.Google Scholar
31. PAULY, M., AND GROSS, M. Spectral Processing of Point-Sampled Geometry. In Proceedings of SIGGRAPH (2001), pp.379-386. Google Scholar
32. PINKALL, U., AND POLTHIER, K. Computing Discrete Minimal Surfaces and Conjugates. Experimental Mathematics 2(1) (1993), pp. 15-36.Google Scholar
33. RASSINEUX, A., VILLON, P., SAVIGNAT, J.-M., AND STAB, O. Surface Remeshing by Local Hermite Diffuse Interpolation. International Journal for numerical methods in Engineering 49 (2000), pp.31-49.Google Scholar
34. SHEFFER, A. Spanning Tree Seams for Reducing Parameterization Distortion of Triangulated Surfaces. In Proceedings of Shape Modeling International (2002). to appear. Google Scholar
35. SHEWCHUK, J. R. Triangle: Engineering a 2D Quality Mesh Generator and Delaunay Triangulator. In Proceedings of the First workshop on Applied Computational Geometry, Philadelphia, Pennsylvania (1996), pp. 123-133. Google Scholar
36. SIMPSON, R. B. Anisotropic Mesh Transformations and Optimal Error Control. Appl. Num. Math. 14(1-3) (1994), pp. 183-198. Google Scholar
37. TRISTANO, J. R., OWEN, S. J., AND CANANN, S. A. Advancing Front Surface Mesh Generation in Parametric Space Using a Riemannian Surface Definition. In Proceedings of 7th International Meshing Roundtable, Sandia National Labs (oct 1998), pp.429-445.Google Scholar
38. TURK, G. Re-Tiling Polygonal Surfaces. In Proceedings of SIGGRAPH (1992), pp.55-64. Google Scholar
39. ULICHNEY, R. A. Dithering with Blue Noise. In Proceedings of the IEEE (1988), vol. 76(1), pp.56-79.Google Scholar
40. VAN DAMME, R., AND ABOUL, L. Tight Triangulations. Mathematical Methods for Curves and Surfaces (1995).Google Scholar
41. VORSATZ, J., RÖSSL, C., KOBBELT, L., AND SEIDEL, H.-P. Feature Sensitive Remeshing. In Eurographics proceedings (sep 2001), pp. 393-401.Google Scholar