“Integer-only cross field computation” by Farchi and Ben-Chen
Conference:
Type(s):
Entry Number: 91
Title:
- Integer-only cross field computation
Session/Category Title: Fields and Remeshing
Presenter(s)/Author(s):
Moderator(s):
Abstract:
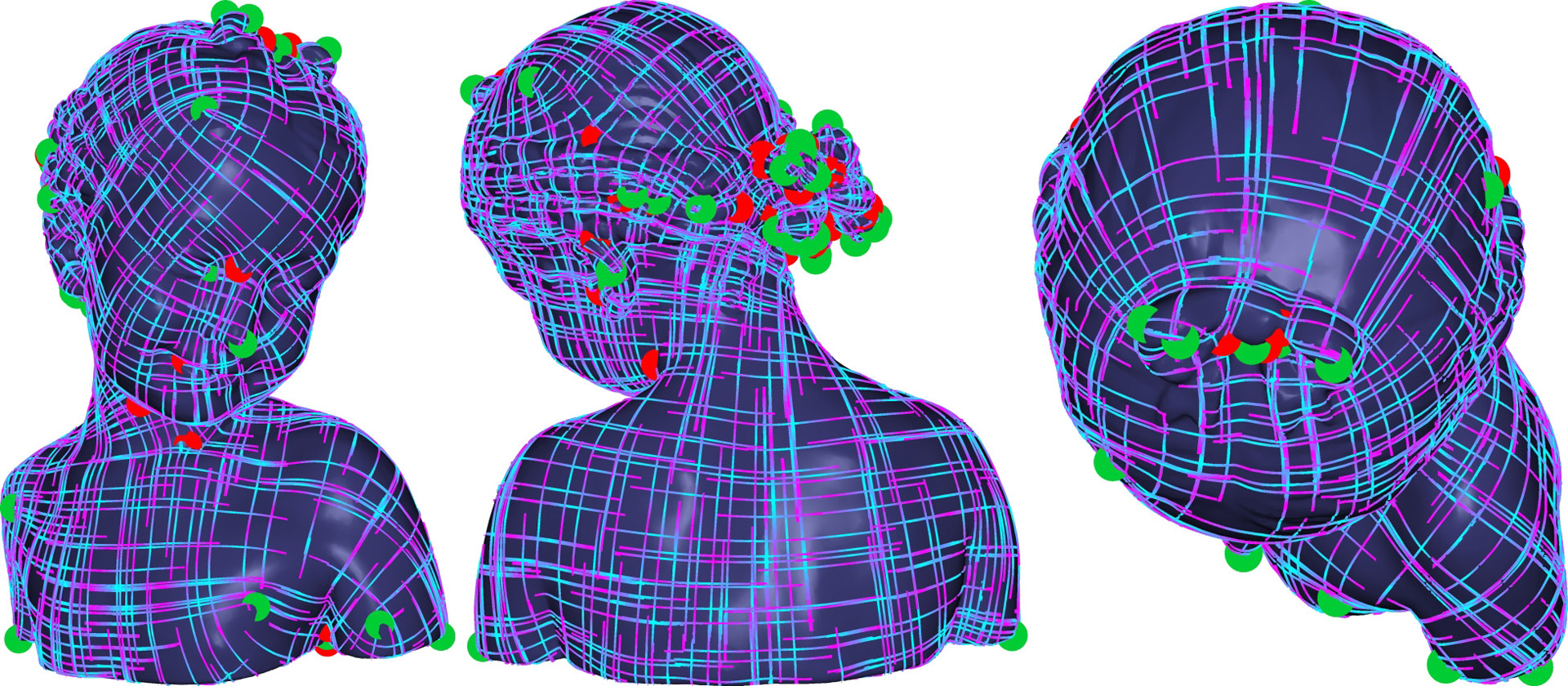
We propose a new iterative algorithm for computing smooth cross fields on triangle meshes that is simple, easily parallelizable on the GPU, and finds solutions with lower energy and fewer cone singularities than state-of-the-art methods. Our approach is based on a formal equivalence, which we prove, between two formulations of the optimization problem. This equivalence allows us to eliminate the real variables and design an efficient grid search algorithm for the cone singularities. We leverage a recent graph-theoretical approximation of the resistance distance matrix of the triangle mesh to speed up the computation and enable a trade-off between the computation time and the smoothness of the output.
References:
1. Dimitris Achlioptas. 2001. Database-friendly random projections. In Proceedings of the twentieth ACM SIGMOD-SIGACT-SIGART symposium on Principles of database systems. ACM, 274–281. Google ScholarDigital Library
2. Erik Agrell, Thomas Eriksson, Alexander Vardy, and Kenneth Zeger. 2002. Closest point search in lattices. IEEE transactions on information theory 48, 8 (2002), 2201–2214. Google ScholarDigital Library
3. Mirela Ben-Chen, Craig Gotsman, and Guy Bunin. 2008. Conformal flattening by curvature prescription and metric scaling. In Computer Graphics Forum, Vol. 27. Wiley Online Library, 449–458.Google Scholar
4. Béla Bollobás. 2013. Modern graph theory. Vol. 184. Springer Science & Business Media.Google Scholar
5. David Bommes, Henrik Zimmer, and Leif Kobbelt. 2009. Mixed-integer quadrangulation. ACM Transactions On Graphics (TOG) 28, 3 (2009), 77. Google ScholarDigital Library
6. Alon Bright, Edward Chien, and Ofir Weber. 2017. Harmonic global parametrization with rational holonomy. ACM Transactions on Graphics (TOG) 36, 4 (2017), 89. Google ScholarDigital Library
7. Marcel Campen and Denis Zorin. 2017a. On Discrete Conformal Seamless Similarity Maps. arXiv preprint arXiv:1705.02422 (2017).Google Scholar
8. Marcel Campen and Denis Zorin. 2017b. Similarity Maps and Field-Guided T-Splines: a Perfect Couple. ACM Trans. Graph 36, 4 (2017). Google ScholarDigital Library
9. Ashok K Chandra, Prabhakar Raghavan, Walter L Ruzzo, Roman Smolensky, and Prasoon Tiwari. 1996. The electrical resistance of a graph captures its commute and cover times. Computational Complexity 6, 4 (1996), 312–340.Google ScholarCross Ref
10. Keenan Crane, Fernando De Goes, Mathieu Desbrun, and Peter Schröder. 2013. Digital geometry processing with discrete exterior calculus. In ACM SIGGRAPH 2013 Courses. ACM, 7. Google ScholarDigital Library
11. Keenan Crane, Mathieu Desbrun, and Peter Schröder. 2010. Trivial connections on discrete surfaces. In Computer Graphics Forum, Vol. 29. 1525–1533.Google ScholarCross Ref
12. Sanjoy Dasgupta and Anupam Gupta. 2003. An elementary proof of a theorem of Johnson and Lindenstrauss. Random Structures & Algorithms 22, 1 (2003), 60–65. Google ScholarDigital Library
13. Timothy A Davis. 2013. Algorithm 930: FACTORIZE: An object-oriented linear system solver for MATLAB. ACM Transactions on Mathematical Software (TOMS) 39, 4 (2013), 28. Google ScholarDigital Library
14. Olga Diamanti, Amir Vaxman, Daniele Panozzo, and Olga Sorkine-Hornung. 2014. Designing N-PolyVector Fields with Complex Polynomials. In Computer Graphics Forum, Vol. 33. Wiley Online Library, 1–11. Google ScholarDigital Library
15. Peter G Doyle and J Laurie Snell. 1984. Random walks and electric networks. Mathematical Association of America,.Google Scholar
16. Hans-Christian Ebke, David Bommes, Marcel Campen, and Leif Kobbelt. 2013. QEx: robust quad mesh extraction. ACM Transactions on Graphics (TOG) 32, 6 (2013), 168. Google ScholarDigital Library
17. David Eppstein. 2003. Dynamic generators of topologically embedded graphs. In Proceedings of the fourteenth annual ACM-SIAM symposium on Discrete algorithms. Society for Industrial and Applied Mathematics, 599–608. Google ScholarDigital Library
18. Alec Jacobson, Daniele Panozzo, et al. 2016. libigl: A simple C++ geometry processing library. (2016). http://libigl.github.io/libigl/.Google Scholar
19. Wenzel Jakob, Marco Tarini, Daniele Panozzo, and Olga Sorkine-Hornung. 2015. Instant field-aligned meshes. ACM Transactions on Graphics (TOG) 34, 6 (2015), 189. Google ScholarDigital Library
20. William B Johnson and Joram Lindenstrauss. 1984. Extensions of Lipschitz mappings into a Hilbert space. Contemporary mathematics 26, 189–206 (1984), 1.Google Scholar
21. G Kirchhoff. 1958. On the solution of the equations obtained from the investigation of the linear distribution of galvanic currents. IRE transactions on circuit theory 5, 1 (1958), 4–7.Google Scholar
22. Felix Knöppel, Keenan Crane, Ulrich Pinkall, and Peter Schröder. 2013. Globally optimal direction fields. ACM Transactions on Graphics (TOG) 32, 4 (2013), 59. Google ScholarDigital Library
23. Christian Liebchen and Romeo Rizzi. 2007. Classes of cycle bases. Discrete Applied Mathematics 155, 3 (2007), 337–355. Google ScholarDigital Library
24. Mark Meyer, Mathieu Desbrun, Peter Schröder, and Alan H Barr. 2003. Discrete differential-geometry operators for triangulated 2-manifolds. In Visualization and mathematics III. Springer, 35–57.Google Scholar
25. Daniele Micciancio. 2001. The hardness of the closest vector problem with preprocessing. IEEE Transactions on Information Theory 47, 3 (2001), 1212–1215. Google ScholarDigital Library
26. Ashish Myles, Nico Pietroni, and Denis Zorin. 2014. Robust field-aligned global parametrization. ACM Transactions on Graphics (TOG) 33, 4 (2014), 135. Google ScholarDigital Library
27. Ashish Myles and Denis Zorin. 2012. Global parametrization by incremental flattening. ACM Transactions on Graphics (TOG) 31, 4 (2012), 109. Google ScholarDigital Library
28. Ashish Myles and Denis Zorin. 2013. Controlled-distortion constrained global parametrization. ACM Transactions on Graphics (TOG) 32, 4 (2013), 105. Google ScholarDigital Library
29. Giuseppe Patané and Michela Spagnuolo. 2013. An interactive analysis of harmonic and diffusion equations on discrete 3D shapes. Computers & Graphics 37, 5 (2013), 526–538. Google ScholarDigital Library
30. Chi-Han Peng, Eugene Zhang, Yoshihiro Kobayashi, and Peter Wonka. 2011. Connectivity editing for quadrilateral meshes. In ACM Transactions on Graphics (TOG), Vol. 30. ACM, 141. Google ScholarDigital Library
31. Nicolas Ray, Wan Chiu Li, Bruno Lévy, Alla Sheffer, and Pierre Alliez. 2006. Periodic global parameterization. ACM Transactions on Graphics (TOG) 25, 4 (2006), 1460–1485. Google ScholarDigital Library
32. Nicolas Ray, Bruno Vallet, Wan Chiu Li, and Bruno Lévy. 2008. N-symmetry direction field design. ACM Transactions on Graphics (TOG) 27, 2 (2008), 10. Google ScholarDigital Library
33. Saeid Sahraei and Michael Gastpar. 2017. Polynomially solvable instances of the shortest and closest vector problems with applications to compute-and-forward. IEEE Transactions on Information Theory 63, 12 (2017), 7780–7792.Google ScholarCross Ref
34. Daniel A Spielman and Nikhil Srivastava. 2011. Graph sparsification by effective resistances. SIAM J. Comput. 40, 6 (2011), 1913–1926. Google ScholarDigital Library
35. Boris Springborn, Peter Schröder, and Ulrich Pinkall. 2008. Conformal equivalence of triangle meshes. In ACM Transactions on Graphics (TOG), Vol. 27. ACM, 77. Google ScholarDigital Library
36. Yiying Tong, Santiago Lombeyda, Anil N Hirani, and Mathieu Desbrun. 2003. Discrete multiscale vector field decomposition. In ACM transactions on graphics (TOG), Vol. 22. ACM, 445–452. Google ScholarDigital Library
37. Amir Vaxman, Marcel Campen, Olga Diamanti, Daniele Panozzo, David Bommes, Klaus Hildebrandt, and Mirela Ben-Chen. 2016. Directional Field Synthesis, Design, and Processing. Computer Graphics Forum (2016).Google Scholar