“Injective and bounded distortion mappings in 3D” by Aigerman and Lipman
Conference:
Type(s):
Title:
- Injective and bounded distortion mappings in 3D
Session/Category Title: Deformation & Distortion
Presenter(s)/Author(s):
Moderator(s):
Abstract:
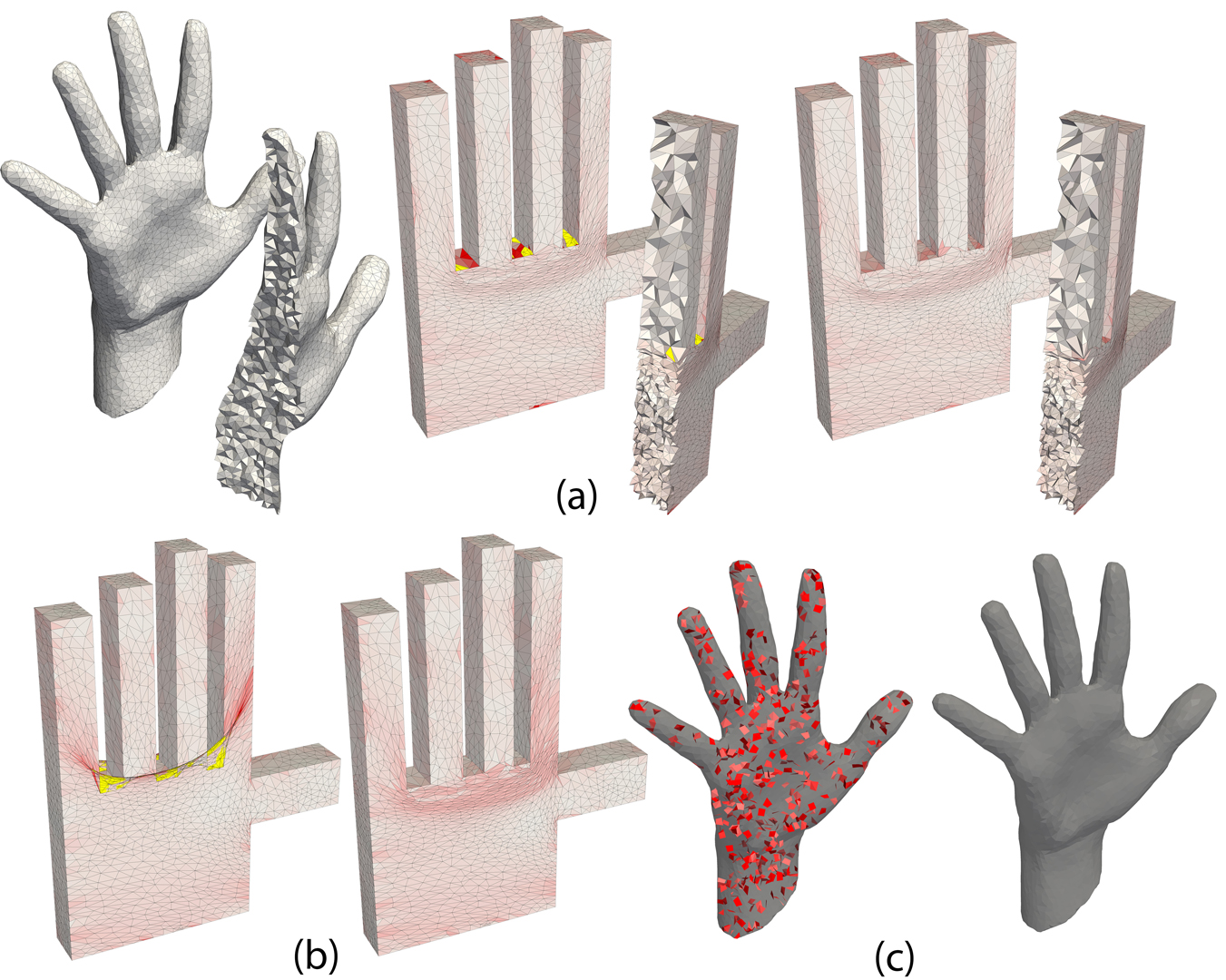
We introduce an efficient algorithm for producing provably injective mappings of tetrahedral meshes with strict bounds on their tetrahedra aspect-ratio distortion.The algorithm takes as input a simplicial map (e.g., produced by some common deformation or volumetric parameterization technique) and projects it on the space of injective and bounded-distortion simplicial maps. Namely, finds a similar map that is both bijective and bounded-distortion. As far as we are aware, this is the first algorithm to produce injective or bounded-distortion simplicial maps of tetrahedral meshes. The construction of the algorithm was made possible due to a novel closed-form solution to the problem of finding the closest orientation-preserving bounded-distortion matrix to an arbitrary matrix in three (and higher) dimensions.The algorithm is shown to have quadratic convergence, usually not requiring more than a handful of iterations to converge. Furthermore, it is readily generalized to simplicial maps of any dimension, including mixed dimensions. Finally, it can deal with different distortion spaces, such as bounded isometric distortion. During experiments we found the algorithm useful for producing bijective and bounded-distortion volume parameterizations and deformations of tetrahedral meshes, and improving tetrahedral meshes, increasing the tetrahedra quality produced by state-of-the-art techniques.
References:
1. Alliez, P., Cohen-Steiner, D., Yvinec, M., and Desbrun, M. 2005. Variational tetrahedral meshing. ACM Trans. Graph. 24, 3 (July), 617–625. Google ScholarDigital Library
2. Ben-Chen, M., Weber, O., and Gotsman, C. 2009. Variational harmonic maps for space deformation. ACM Trans. Graph. 28, 3 (July), 34:1–34:11. Google ScholarDigital Library
3. Botsch, M., and Sorkine, O. 2008. On linear variational surface deformation methods. Visualization and Computer Graphics, IEEE Transactions on 14, 1, 213–230. Google ScholarDigital Library
4. Bronstein, A., Bronstein, M., and Kimmel, R. 2008. Numerical Geometry of Non-Rigid Shapes, 1 ed. Springer Publishing Company, Incorporated. Google ScholarDigital Library
5. Cascón, J., Montenegro, R., Escobar, J., Rodríguez, E., and Montero, G. 2009. The meccano method for automatic tetrahedral mesh generation of complex genus-zero solids. In Proceedings of the 18th International Meshing Roundtable. Springer, 463–480.Google Scholar
6. Cgal. Cgal, computational geometry algorithms library. http://www.cgal.org.Google Scholar
7. Chao, I., Pinkall, U., Sanan, P., and Schröder, P. 2010. A simple geometric model for elastic deformations. ACM Trans. Graph. 29, 4 (July), 38:1–38:6. Google ScholarDigital Library
8. Coquillart, S. 1990. Extended free-form deformation: a sculpturing tool for 3D geometric modeling, vol. 24. ACM. Google ScholarDigital Library
9. Dacorogna, B., and Maréchal, P. 2007. Convex so (n) x so (n)-invariant functions and refinements of von neumann’s inequality. In ANNALES-FACULTE DES SCIENCES TOULOUSE MATHEMATIQUES, vol. 16, Université Paul Sabatier, 71.Google Scholar
10. Eck, M., DeRose, T., Duchamp, T., Hoppe, H., Lounsbery, M., and Stuetzle, W. 1995. Multiresolution analysis of arbitrary meshes. In Proceedings of the 22nd annual conference on Computer graphics and interactive techniques, ACM, New York, NY, USA, SIGGRAPH ’95, 173–182. Google ScholarDigital Library
11. Eppstein, D. 2001. Global optimization of mesh quality. Tutorial at the 10th Int.Google Scholar
12. Floater, M. S., and Pham-Trong, V. 2006. Convex combination maps over triangulations, tilings, and tetrahedral meshes. Adv. Comput. Math. 25, 4, 347–356.Google ScholarCross Ref
13. Floater, M. S., Kós, G., and Reimers, M. 2005. Mean value coordinates in 3d. Comput. Aided Geom. Des. 22, 7 (Oct.), 623–631. Google ScholarDigital Library
14. Floater, M. S. 2003. One-to-one piecewise linear mappings over triangulations. Math. Comput. 72, 242, 685–696. Google ScholarDigital Library
15. Freitag, L. A., and Knupp, P. M., 2002. Tetrahedral mesh improvement via optimization of the element condition number.Google Scholar
16. Gregson, J., Sheffer, A., and Zhang, E. 2011. All-hex mesh generation via volumetric polycube deformation. Computer Graphics Forum (Special Issue of Symposium on Geometry Processing 2011) 30, 5, to appear.Google Scholar
17. Irving, G., Teran, J., and Fedkiw, R. 2004. Invertible finite elements for robust simulation of large deformation. In Proceedings of the 2004 ACM SIGGRAPH/Eurographics symposium on Computer animation, Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, SCA ’04, 131–140. Google ScholarDigital Library
18. Jacobson, A., Baran, I., Popovic, J., and Sorkine, O. 2011. Bounded biharmonic weights for real-time deformation. ACM Trans. Graph. 30, 4, 78. Google ScholarDigital Library
19. Johnen, A., Remacle, J.-F., and Geuzaine, C. 2012. Geometrical validity of high-order triangular finite elements. Engineering with Computers, 1–8.Google Scholar
20. Joshi, P., Meyer, M., DeRose, T., Green, B., and Sanocki, T. 2007. Harmonic coordinates for character articulation. ACM Trans. Graph. 26, 3 (July). Google ScholarDigital Library
21. Ju, T., Schaefer, S., and Warren, J. 2005. Mean value coordinates for closed triangular meshes. ACM Trans. Graph. 24, 3 (July), 561–566. Google ScholarDigital Library
22. Klingner, B. M., and Shewchuk, J. R. 2007. Agressive tetrahedral mesh improvement. In Proceedings of the 16th International Meshing Roundtable, 3–23.Google Scholar
23. Labelle, F., and Shewchuk, J. R. 2007. Isosurface stuffing: Fast tetrahedral meshes with good dihedral angles. ACM Transactions on Graphics 26, 3 (July), 57.1–57.10. Special issue on Proceedings of SIGGRAPH 2007. Google ScholarDigital Library
24. Lévy, B., Petitjean, S., Ray, N., and Maillot, J. 2002. Least squares conformal maps for automatic texture atlas generation. ACM Trans. Graph. 21, 3 (July), 362–371. Google ScholarDigital Library
25. Li, X., Guo, X., Wang, H., He, Y., Gu, X., and Qin, H. 2007. Harmonic volumetric mapping for solid modeling applications. In Proceedings of the 2007 ACM symposium on Solid and physical modeling, ACM, New York, NY, USA, SPM ’07, 109–120. Google ScholarDigital Library
26. Lipman, Y., Levin, D., and Cohen-Or, D. 2008. Green coordinates. ACM Trans. Graph. 27, 3 (Aug.), 78:1–78:10. Google ScholarDigital Library
27. Lipman, Y. 2012. Bounded distortion mapping spaces for triangular meshes. ACM Trans. Graph. 31, 4 (July), 108:1–108:13. Google ScholarDigital Library
28. Liu, L., Zhang, L., Xu, Y., Gotsman, C., and Gortler, S. 2008. A local/global approach to mesh parameterization. In Computer Graphics Forum, vol. 27, Wiley Online Library, 1495–1504. Google ScholarDigital Library
29. Meyer, M., Desbrun, M., Schröder, P., and Barr, A. 2002. Discrete differential-geometry operators for triangulated 2-manifolds. Visualization and mathematics 3, 7, 34–57.Google Scholar
30. Müller, M., Dorsey, J., McMillan, L., Jagnow, R., and Cutler, B. 2002. Stable real-time deformations. In Proceedings of the 2002 ACM SIGGRAPH/Eurographics symposium on Computer animation, ACM, 49–54. Google ScholarDigital Library
31. Owen, S. 1998. A survey of unstructured mesh generation technology. In 7th International Meshing Roundtable, vol. 3.Google Scholar
32. Sederberg, T., and Parry, S. 1986. Free-form deformation of solid geometric models. In ACM Siggraph Computer Graphics, vol. 20, ACM, 151–160. Google ScholarDigital Library
33. Shewchuk, J. R. 2012. Combinatorial Scientific Computing. CRC Press, January, ch. Unstructured Mesh Generation, chapter 10, 257–297.Google Scholar
34. Sorkine, O., and Alexa, M. 2007. As-rigid-as-possible surface modeling. In Proceedings of the fifth Eurographics symposium on Geometry processing, Eurographics Association, Aire-la-Ville, Switzerland, Switzerland, SGP ’07, 109–116. Google ScholarDigital Library
35. Stewart, G. W. 1990. Perturbation theory for the singular value decomposition. In IN SVD AND SIGNAL PROCESSING, II: ALGORITHMS, ANALYSIS AND APPLICATIONS, Elsevier, 99–109.Google Scholar
36. Teng, S.-H., and Wong, C. W. 2000. Unstructured mesh generation: Theory, practice, and perspectives. International Journal of Computational Geometry & Applications 10, 03, 227–266.Google ScholarCross Ref
37. Tournois, J., Wormser, C., Alliez, P., and Desbrun, M. 2009. Interleaving delaunay refinement and optimization for practical isotropic tetrahedron mesh generation. ACM Trans. Graph. 28, 3 (July), 75:1–75:9. Google ScholarDigital Library
38. Wang, Y., Gu, X., Thompson, P. M., and Yau, S. T. 2004. 3d harmonic mapping and tetrahedral meshing of brain imaging data. Proc. Medical Imaging Computing and Computer Assisted Intervention (MICCAI), St. Malo, France, Sept.Google Scholar
39. Wang, Y., Gu, X., Chan, T. F., Thompson, P. M., and Yau, S.-T. 2004. Volumetric harmonic brain mapping. In Proceedings of the 2004 IEEE International Symposium on Biomedical Imaging: From Nano to Macro, Arlington, VA, USA, 15–18 April 2004, IEEE, 1275–1278.Google Scholar
40. Weber, O., Myles, A., and Zorin, D. 2012. Computing extremal quasiconformal maps. Comp. Graph. Forum 31, 5 (Aug.), 1679–1689. Google ScholarDigital Library
41. Xia, J., He, Y., Han, S., Fu, C.-W., Luo, F., and Gu, X. 2010. Parameterization of star-shaped volumes using green’s functions. In Proceedings of the 6th international conference on Advances in Geometric Modeling and Processing, Springer-Verlag, Berlin, Heidelberg, GMP’10, 219–235. Google ScholarDigital Library
42. Xu, H., Yu, W., Gu, S., and Li, X. 2012. Biharmonic volumetric mapping using fundamental solutions. IEEE Transactions on Visualization and Computer Graphics 99, PrePrints, 1. Google ScholarDigital Library