“Improving Regularity of the Centoridal Voronoi Tessellation” by Men, Shen, Khan and Yan
Conference:
Type(s):
Entry Number: 66
Title:
- Improving Regularity of the Centoridal Voronoi Tessellation
Presenter(s)/Author(s):
Abstract:
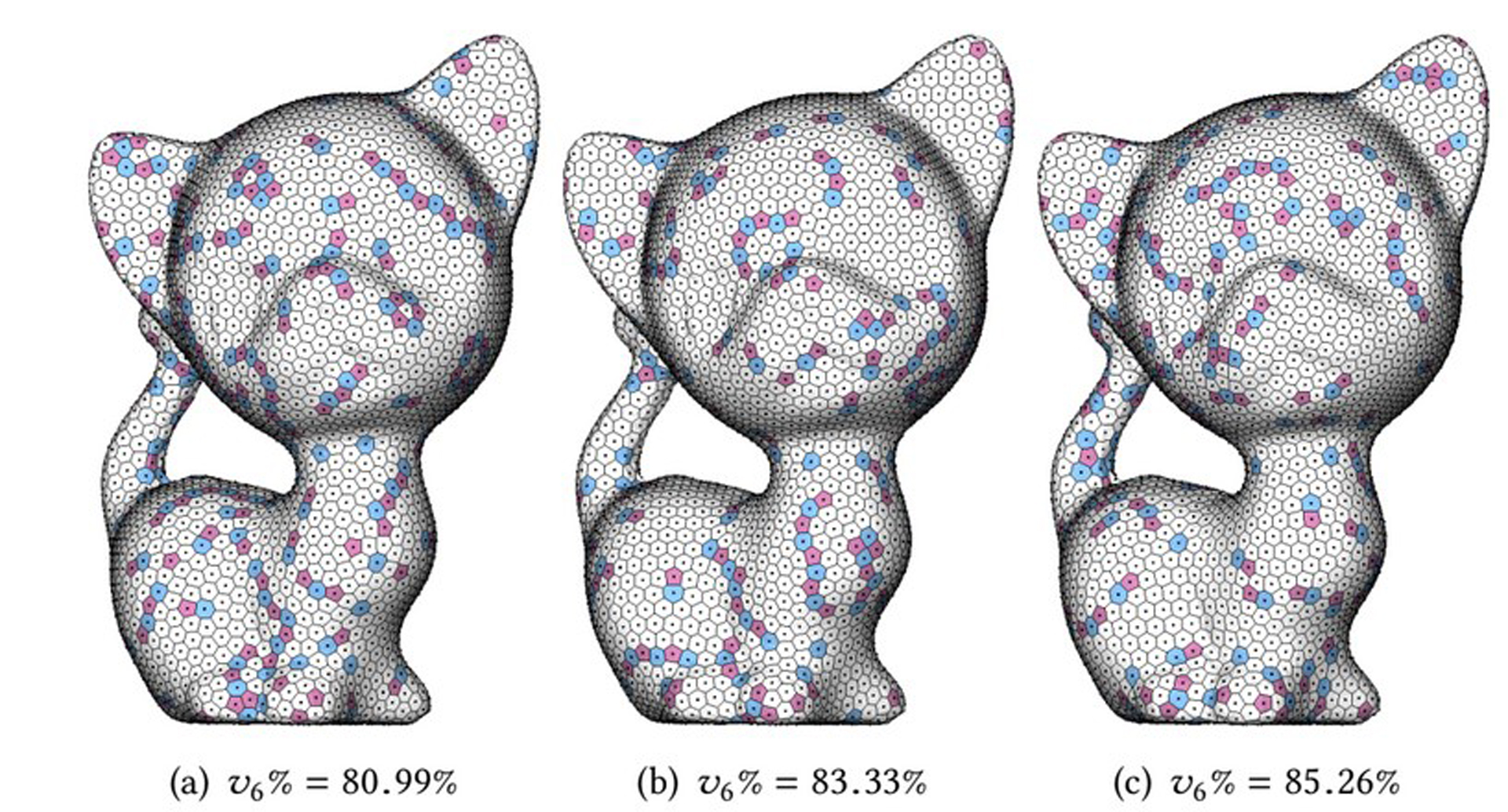
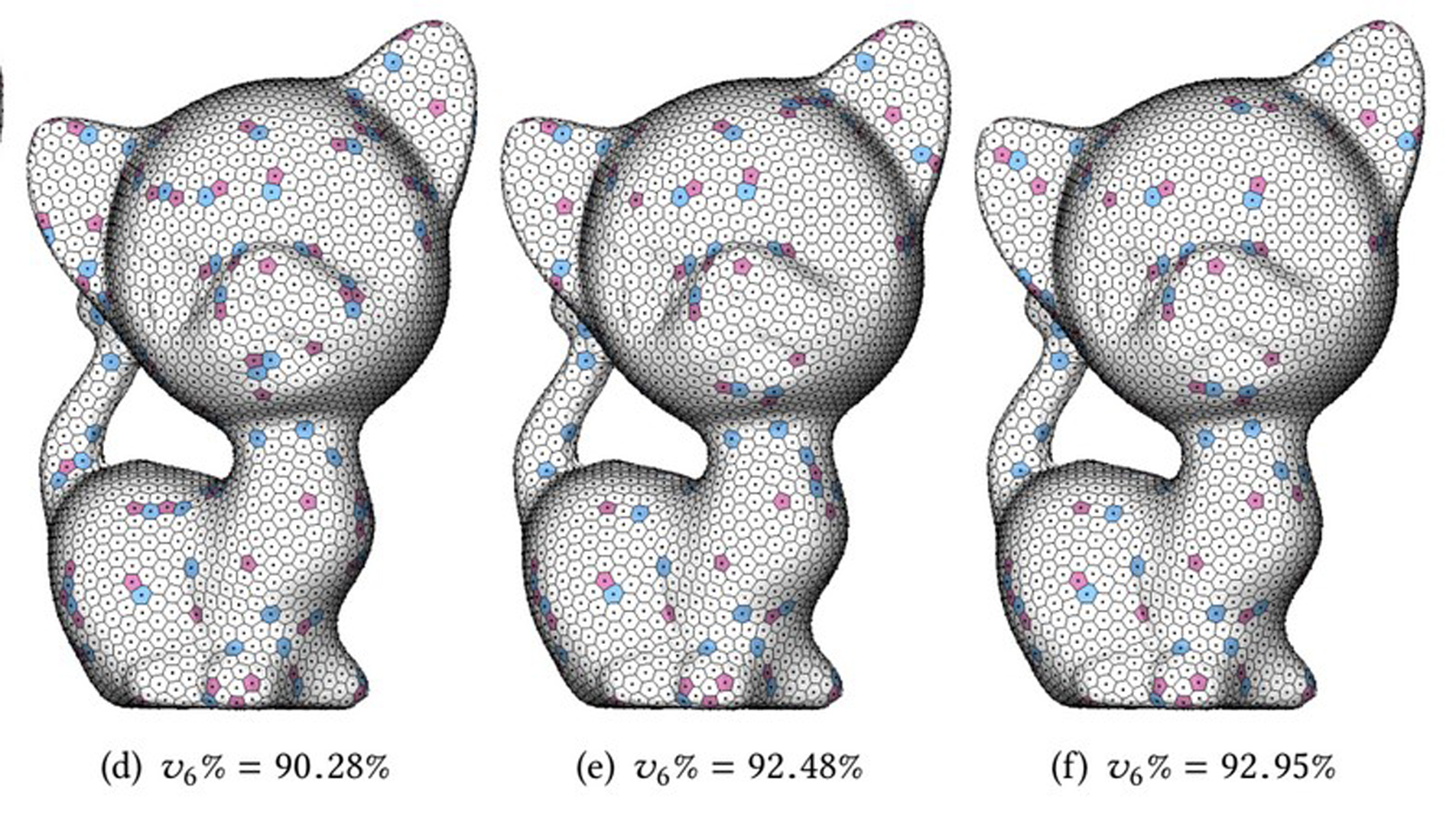
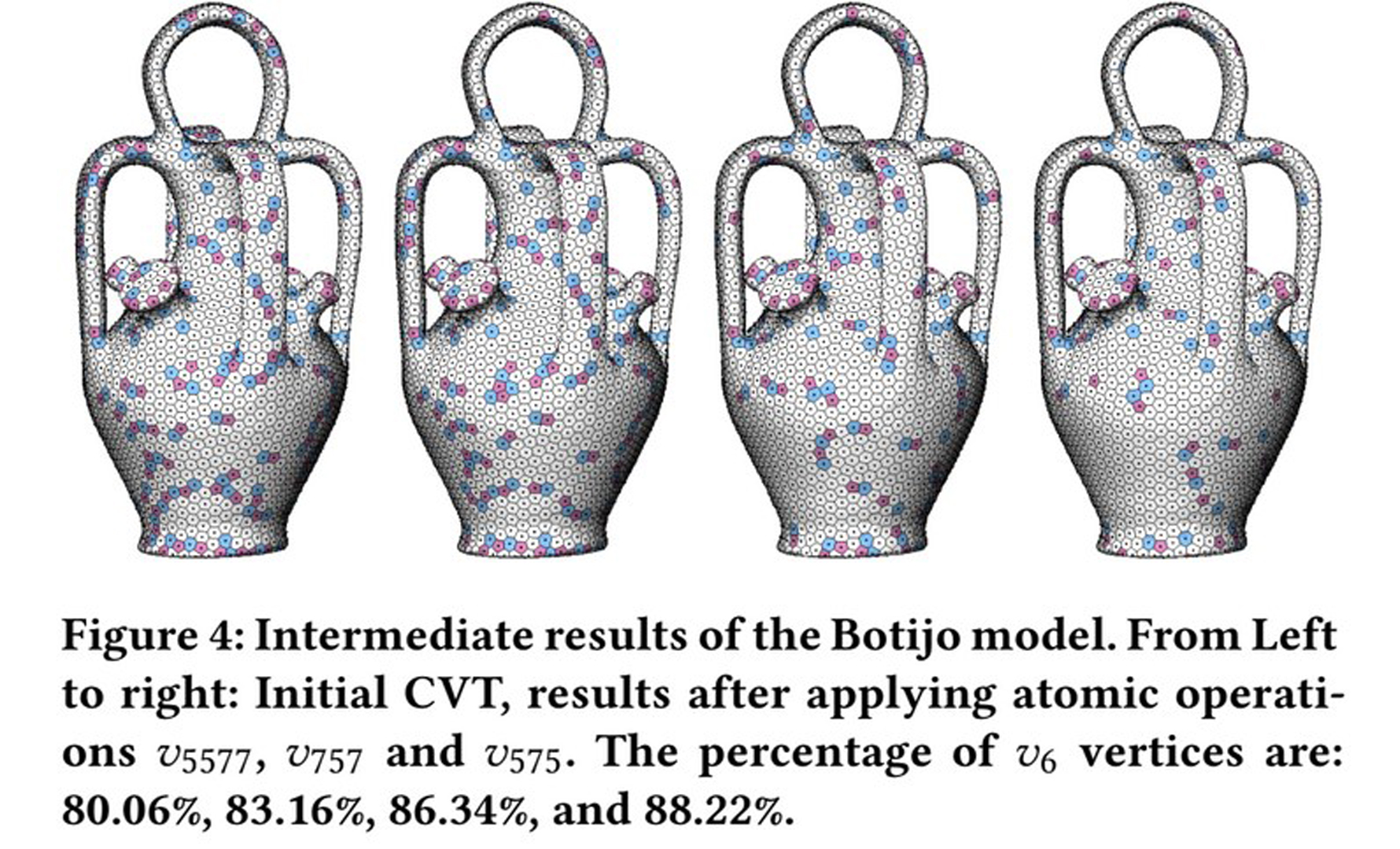
We present a novel method for valence optimization of the Centroidal Voronoi Tessellation (CVT). We first identify three commonly appeared atomic configurations of local irregular Voronoi cells, and then design specific atomic operations for each configuration to improve the regularity within the CVT framework.
References:
- Oliver Deussen, Marc Spicker, and Qian Zheng. 2017. Weighted Linde-buzo-gray Stippling. ACM Trans. Graph. 36, 6, Article 233 (2017), 233:1–233:12 pages.
- Qiang Du, Vance Faber, and Max Gunzburger. 1999. Centroidal Voronoi tessellations: applications and algorithms. SIAM Rev. 41 (1999), 637–676.
- Yuanyuan Li, Eugene Zhang, Yoshihiro Kobayashi, and Peter Wonka. 2010. Editing Operations for Irregular Vertices in Triangle Meshes. ACM Trans. on Graphics (Proc. SIGGRAPH Asia) 29, 6 (2010), 153:1–153:11.
- Yang Liu, Wenping Wang, Bruno Lévy, Feng Sun, Dong-Ming Yan, Lin Lu, and Chenglei Yang. 2009. On Centroidal Voronoi Tessellation – Energy Smoothness and Fast Computation. ACM Trans. on Graphics 28, 4 (2009), 101:1–101:11.
- S. A. Lloyd. 1982. Least squares quantization in PCM. IEEE Transactions on Information Theory 28, 2 (1982), 129–137.
- Lin Lu, Feng Sun, Hao Pan, and Wenping Wang. 2012. Global Optimization of Centroidal Voronoi Tessellation with Monte Carlo Approach. IEEE Trans. on Vis. and Comp. Graphics 18, 11 (2012), 1880–1890.
- L.Wang, Franck Hétroy-Wheeler, and E. Boyer. 2016. A Hierarchical Approach for Regular Centroidal Voronoi Tessellations. Comput. Graph. Forum 35, 1 (2016), 152–165. https://doi.org/10.1111/cgf.12716.
Keyword(s):
Acknowledgements:
This work is partially funded by the National Natural Science Foundation of China (61772523 and 61620106003).