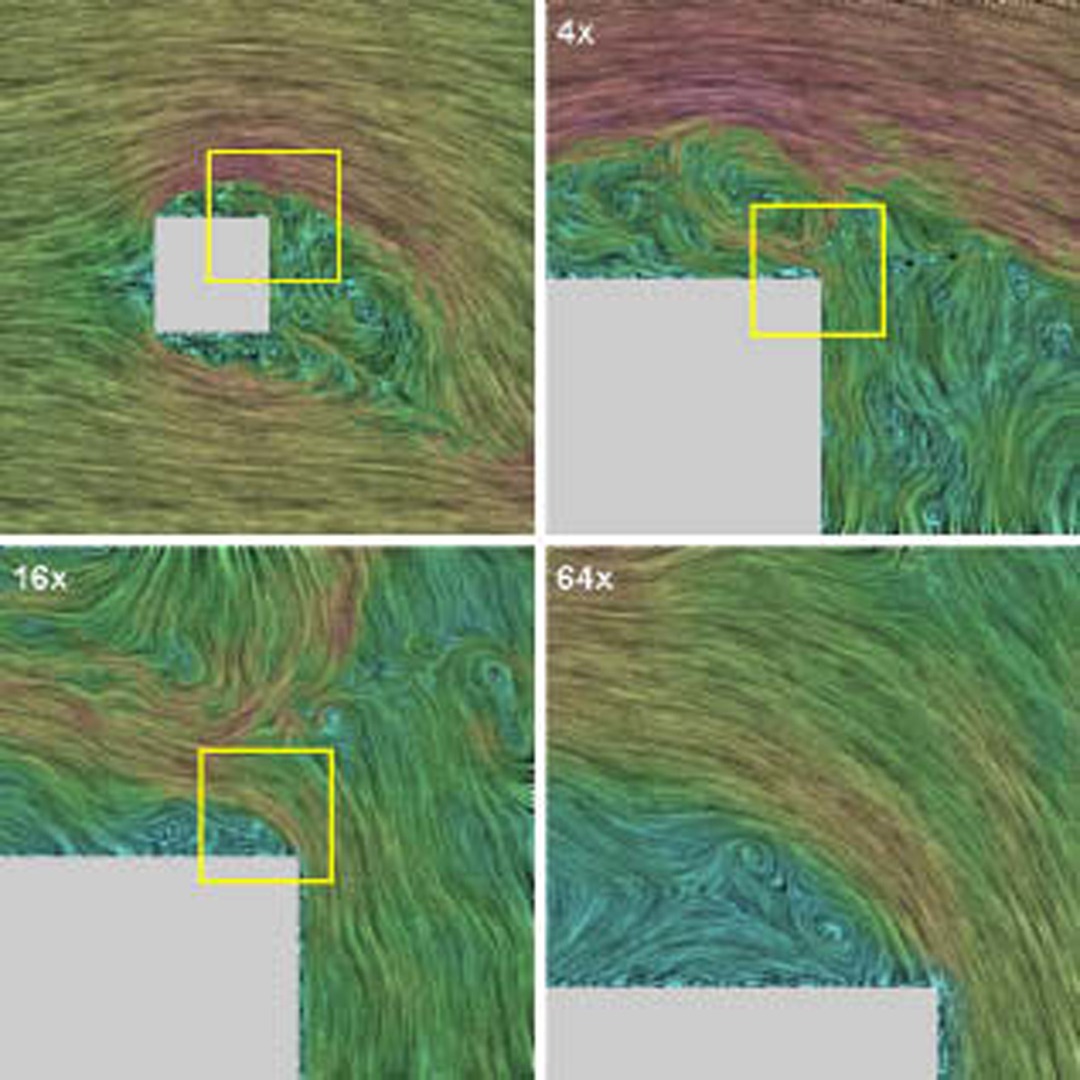
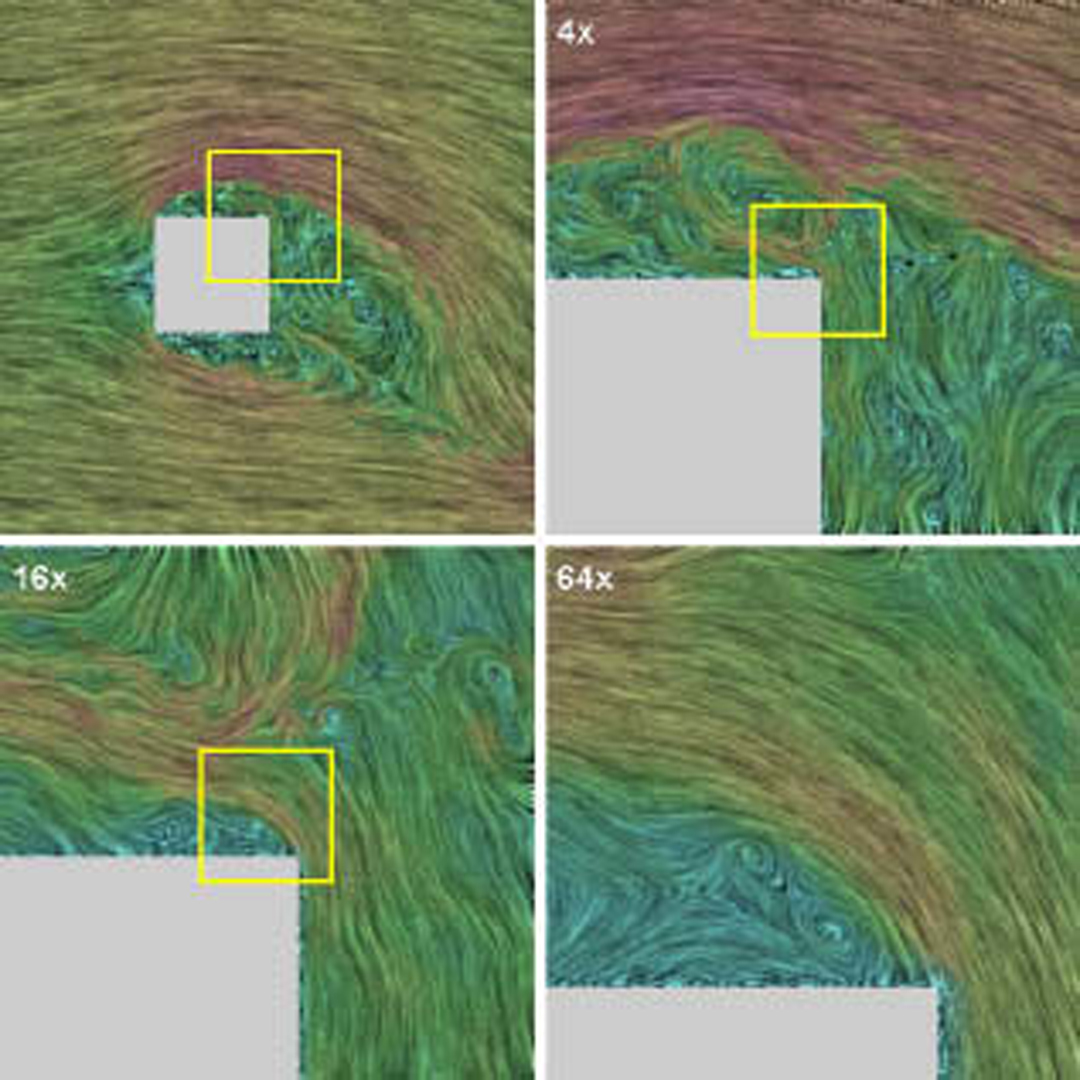
“Image based flow visualization”

A new method for the visualization of two-dimensional fluid flow is presented. The method is based on the advection and decay of dye. These processes are simulated by defining each frame of a flow animation as a blend between a warped version of the previous image and a number of background images. For the latter a sequence of filtered white noise images is used: filtered in time and space to remove high frequency components. Because all steps are done using images, the method is named Image Based Flow Visualization (IBFV). With IBFV a wide variety of visualization techniques can be emulated. Flow can be visualized as moving textures with line integral convolution and spot noise. Arrow plots, streamlines, particles, and topological images can be generated by adding extra dye to the image. Unsteady flows, defined on arbitrary meshes, can be handled. IBFV achieves a high performance by using standard features of graphics hardware. Typically fifty frames per second are generated using standard graphics cards on PCs. Finally, IBFV is easy to understand, analyse, and implement.

1. CABRAL, B., AND LEEDOM, L. C. 1993. Imaging vector fields using line integral convolution. In Proceedings of ACM SIGGRAPH 93, Computer Graphics Proceedings, Annual Conference Series, 263-272. Google Scholar
2. DE LEEUW, W., AND VAN LIERE, R. 1997. Divide and conquer spot noise. In Proceedings SuperComputing’97. Google Scholar
3. DE LEEUW, W., ANDVAN WIJK, J. 1995. Enhanced spot noise for vector field visualization. In Proceedings IEEE Visualization’95. Google Scholar
4. HANSEN, P. 1997. Introducing pixel texture. Developer News, 23-26. Silicon Graphics Inc.Google Scholar
5. HEIDRICH, W., WESTERMANN, R., SEIDEL, H.-P., AND ERTL, T. 1999. Applications of pixel textures in visualization and realistic image synthesis. In ACM Symposium on Interactive 3D Graphics, 127-134. Google Scholar
6. HELMAN, J., AND HESSELINK, L. 1989. Representation and display of vector field topology in fluid flow data sets. Computer 22, 8 (August), 27-36. Google Scholar
7. JOBARD, B., ERLEBACHER, G., AND HUSSAINI, M. 2000. Hardware-accelerated texture advection for unsteady flow visualization. In Proceedings IEEE Visualization 2000, 155-162. Google Scholar
8. JOBARD, B., ERLEBACHER, G., AND HUSSAINI, M. 2001. Lagrangian-eulerian advection for unsteady flow visualization. In Proceedings IEEE Visualization 2001, 53-60. Google Scholar
9. MAX, N., AND BECKER, B. 1995. Flow visualization using moving textures. In Proceedings of the ICASW/LaRC Symposium on Visualizing Time-Varying Data, 77-87.Google Scholar
10. PORTER, T., AND DUFF, T. 1984. Compositing digital images. Computer Graphics 18, 253-259. Proceedings SIGGRAPH’84. Google Scholar
11. SHEN, H.-W., AND KAO, D. L. 1998. A new line integral convolution algorithm for visualizing time-varying flow fields. IEEE Transactions on Visualization and Computer Graphics 4, 2, 98-108. Google Scholar
12. SHEN, H.-W., JOHNSON, C., AND MA, K.-L. 1996. Visualizing vector fields using line integral convolution and dye advection. In Symposium on Volume Visualization, 63-70. Google Scholar
13. STALLING, D., AND HEGE, H.-C. 1995. Fast and resolution independent line integral convolution. In Proceedings of ACM SIGGRAPH 95, Computer Graphics Proceedings, Annual Conference Series, 249-256. Google Scholar
14. VAN WIJK, J. 1991. Spot noise: Texture synthesis for data visualization. Computer Graphics 25, 309-318. Proceedings ACM SIGGRAPH 91. Google Scholar
15. VERSTAPPEN, R., AND VELDMAN, A. 1998. Spectro-consistent discretization of Navier-Stokes: a challenge to RANS and LES. Journal of Engineering Mathematics 34, 1, 163-179.Google Scholar
16. WEISKOPF, D., HOPF, M., AND ERTL, T. 2001. Hardware-accelerated visualization of time-varying 2D and 3D vector fields by texture advection via programmable per-pixel operations. In Vision, Modeling, and Visualization VMV ’01 Conference Proceedings, 439-446. Google Scholar
17. WEJCHERT, J., AND HAUMANN, D. 1991. Animation aerodynamics. Computer Graphics 25, 19-22. Proceedings ACM SIGGRAPH 91. Google Scholar
18. WITTING, P. 1999. Computational fluid dynamics in a traditional animation environment. In Proceedings of ACM SIGGRAPH 99, Computer Graphics Proceedings, Annual Conference Series, 129-136. Google Scholar
19. ZÖCKLER, M., STALLING, D., AND HEGE, H.-C. 1997. Parallel line integral convolution. Parallel Computing 23, 7, 975-989. Google Scholar