“Global non-rigid alignment of 3-D scans” by Brown and Rusinkiewicz

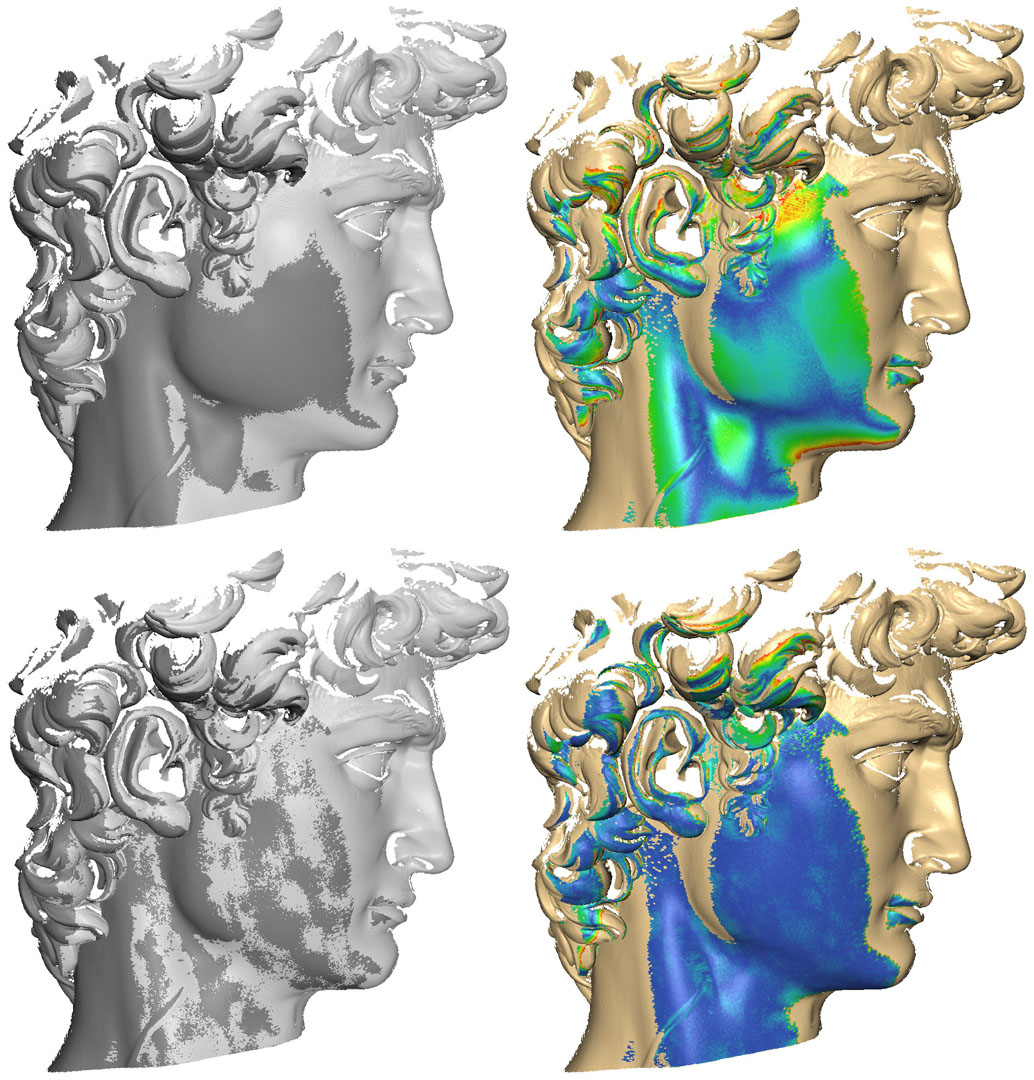
A key challenge in reconstructing high-quality 3D scans is registering data from different viewpoints. Existing global (multiview) alignment algorithms are restricted to rigid-body transformations, and cannot adequately handle non-rigid warps frequently present in real-world datasets. Moreover, algorithms that can compensate for such warps between pairs of scans do not easily generalize to the multiview case. We present an algorithm for obtaining a globally optimal alignment of multiple overlapping datasets in the presence of low-frequency non-rigid deformations, such as those caused by device nonlinearities or calibration error. The process first obtains sparse correspondences between views using a locally weighted, stability-guaranteeing variant of iterative closest points (ICP). Global positions for feature points are found using a relaxation method, and the scans are warped to their final positions using thin-plate splines. Our framework efficiently handles large datasets—thousands of scans comprising hundreds of millions of samples—for both rigid and non-rigid alignment, with the non-rigid case requiring little overhead beyond rigid-body alignment. We demonstrate that, relative to rigid-body registration, it improves the quality of alignment and better preserves detail in 3D datasets from a variety of scanners exhibiting non-rigid distortion.

1. Allen, B., Curless, B., and Popović, Z. 2003. The space of human body shapes: Reconstruction and parameterization from range scans. ACM Trans. Graphics (Proc. SIGGRAPH) 22, 3, 587–594. Google ScholarDigital Library
2. Benjemaa, R., and Schmitt, F. 1998. A solution for the registration of multiple 3d point sets using unit quaternions. In Proc. ECCV. Google ScholarDigital Library
3. Bergevin, R., Soucy, M., Gagnon, H., and Laurendeau, D. 1996. Towards a general multi-view registration technique. IEEE Trans. PAMI 18, 5, 540–547. Google ScholarDigital Library
4. Bernardini, F., Rushmeier, H., Martin, I. M., Mittle-Man, J., and Taubin, G. 2002. Building a digital model of Michelangelo’s Florentine Pietà. IEEE Computer Graphics and Applications 22, 1, 59–67. Google ScholarDigital Library
5. Besl, P. J., and McKay, N. D. 1992. A method for registration of 3-D shapes. IEEE Trans. PAMI 14, 2, 239–256. Google ScholarDigital Library
6. Bookstein, F. L. 1989. Principal warps: Thin-plate splines and the decomposition of deformations. IEEE Trans. PAMI 11, 6 (June), 567 — 585. Google ScholarDigital Library
7. Brown, B., and Rusinkiewicz, S. 2004. Non-rigid range-scan alignment using thin-plate splines. In Proc. 3DPVT. Google ScholarCross Ref
8. Chen, Y., and Medioni, G. 1992. Object modelling by registration of multiple range images. Image and Vision Computing 10, 3, 145–155. Google ScholarDigital Library
9. Chui, H., and Rangarajan, A. 2003. A new point matching algorithm for non-rigid registration. CVIU 89, 2–3 (February-March), 114–141. Google ScholarDigital Library
10. Curless, B., and Levoy, M. 1996. A volumetric method for building complex models from range images. In Proceedings of the 23rd Annual Conference on Computer Graphics and Interactive Techniques, ACM Press, 303–312. Google ScholarDigital Library
11. Duchon, J. 1977. Splines minimizing rotation-invariant seminorms in Sobolev spaces. In Constructive Theory of Functions of Several Variables, Springer-Verlag, Berlin, 85–100.Google Scholar
12. Gelfand, N., Ikemoto, L., Rusinkiewicz, S., and Levoy, M. 2003. Geometrically stable sampling for the ICP algorithm. In Proc. 3DIM.Google Scholar
13. Hähnel, D., Thrun, S., and Burgard, W. 2003. An extension of the ICP algorithm for modeling nonrigid objects with mobile robots. In Proc. IJCAI, IJCAI. Google ScholarDigital Library
14. Huang, Q.-X., Flöry, S., Gelfand, N., Hofer, M., and Pottmann, H. 2006. Reassembling fractured objects by geometric matching. In SIGGRAPH ’06: ACM SIGGRAPH 2006 Papers, ACM Press, New York, NY, USA, 569–578. Google ScholarDigital Library
15. Ikemoto, L., Gelfand, N., and Levoy, M. 2003. A hierarchical method for aligning warped meshes. In Proc. 3DIM.Google Scholar
16. Jian, B., and Vemuri, B. 2005. A robust algorithm for point set registration using mixture of gaussians. In Proc. ICCV. Google ScholarDigital Library
17. Krishnan, S., Lee, P., Moore, J., and Venkatasubramanian, S. 2005. Simultaneous registration of multiple 3d point sets via optimization on a manifold. In Proc. Symposium on Geometry Processing. Google ScholarDigital Library
18. Levoy, M., Pulli, K., Curless, B., Rusinkiewicz, S., Koller, D., Pereira, L., Ginzton, M., Anderson, S., Davis, J., Ginsberg, J., Shade, J., and Fulk, D. 2000. The Digital Michelangelo Project: 3-D scanning of large statues. In Proc. SIGGRAPH. Google ScholarDigital Library
19. Li, X., and Guskov, I. 2005. Multiscale features for approximate alignment of point-based surfaces. In Symposium on Geometry Processing, 217–226. Google ScholarDigital Library
20. Nehab, D., Rusinkiewicz, S., Davis, J., and Ramamoorthi, R. 2005. Efficiently combining positions and normals for precise 3D geometry. ACM Transactions on Graphics (Proc. SIGGRAPH) 24, 3 (Aug.). Google ScholarDigital Library
21. Neugebauer, P. J. 1997. Geometrical cloning of 3D objects via simultaneous registration of multiple range images. In Proc. SMA, IEEE Computer Society, 130. Google ScholarDigital Library
22. Pulli, K. 1999. Multiview registration for large data sets. In Proc. 3DIM. Google ScholarDigital Library
23. Rusinkiewicz, S. 2001. Efficient variants of the ICP algorithm. In Proc. 3DIM.Google ScholarCross Ref
24. Shum, H.-Y, and Szeliski, R. 2000. Construction of panoramic mosaics with global and local alignment. International Journal of Computer Vision 36, 2, 101–130. Google ScholarDigital Library
25. Sorkine, O., Lipman, Y., Cohen-Or, D., Alexa, M., Rössl, C., and Seidel, H.-P. 2004. Laplacian surface editing. In Proceedings of the Eurographics/ACM SIGGRAPH Symposium on Geometry Processing, ACM Press, 179–188. Google ScholarDigital Library
26. Wahba, G. 1990. Spline Models for Observational Data. Society for Industrial and Applied Mathematics, Philadelphia, PA, ch. 2.4.Google Scholar
27. Wen, G., Zhu, D., Xia, S., and Wang, Z. 2005. Total least squares fitting of point sets in m-d. In Computer Graphics International. Google ScholarDigital Library
28. Williams, J., and Bennamoun, M. 2000. A multiple view 3D registration algorithm with statistical error modeling. IEICE Transactions on Information and Systems E83-D(8) (August), 1662–1670.Google Scholar
29. Woodham, R. J. 1980. Photometric method for determining surface orientation from multiple images. Optical Engineering 19, 1, 139–144.Google ScholarCross Ref