“Geometric modeling of solid objects by using a face adjacency graph representation” by Falcidieno, De Floriani and Ansaldi
Conference:
Type(s):
Title:
- Geometric modeling of solid objects by using a face adjacency graph representation
Presenter(s)/Author(s):
Abstract:
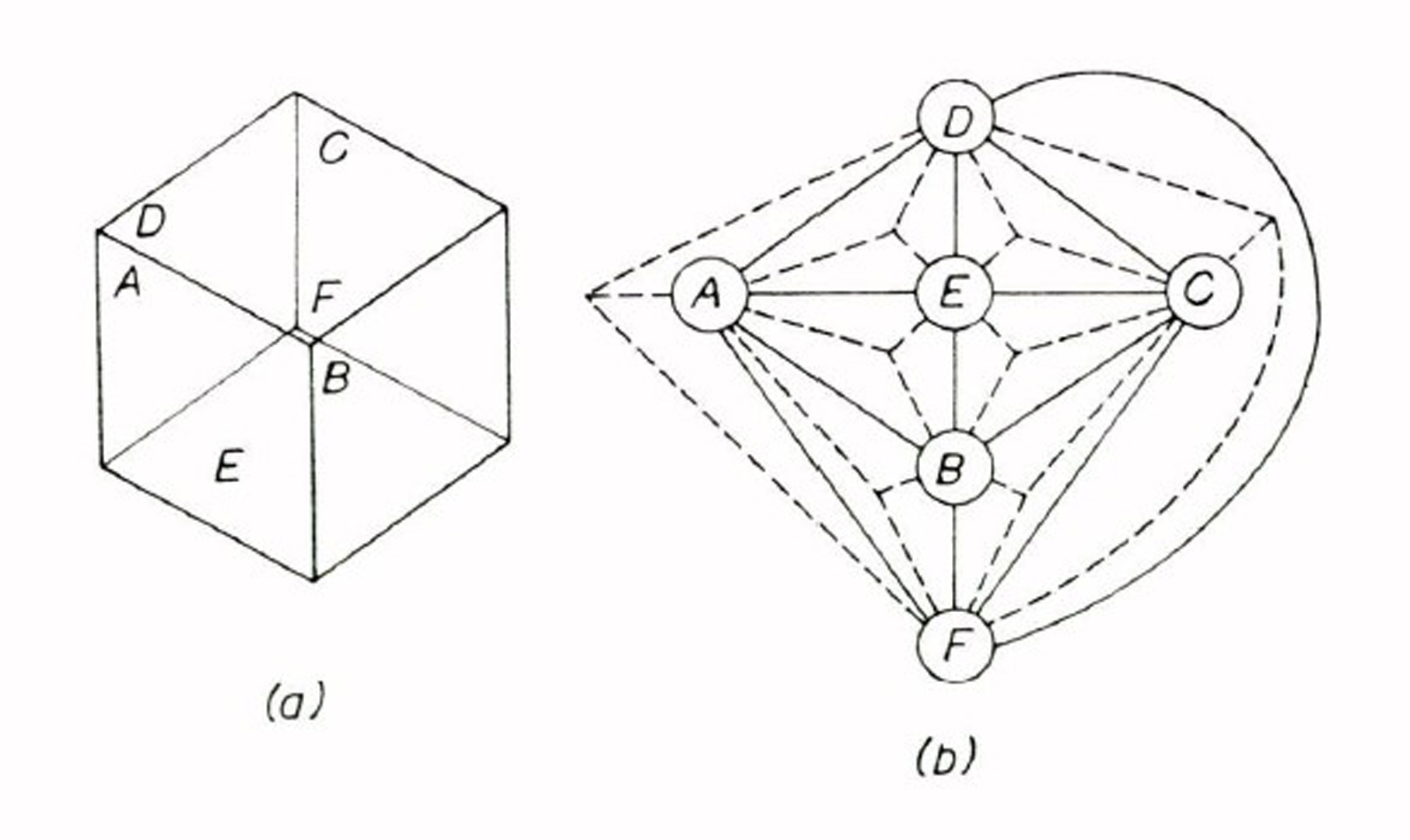
A relational graph structure based on a boundary representation of solid objects is described. In this structure, called face adjacency graph, nodes represent object faces, whereas edges and vertices are encoded into arcs and hyperarcs. Based on the face adjacency graph, we define a set of primitive face-oriented Euler operators, and a set of macrooperators for face manipulation, which allow a compact definition and an efficient updating of solid objects. We briefly describe a hierarchical graph structure based on the face adjacency graph, which provides a representation of an object at different levels of detail. Thus it is consistent with the stepwise refinement process through which the object description is produced.
References:
1. Ancona, M., De Floriani, L., Trebino, O., Zamana,A., “A System for Defining Structured Graphs”, Rivista di Informatica,1984, to appear.
2. Ansaldi, S., De Floriani, L., Falcidieno, B., “Edge-face Graph Representations of Solid Objects”, Proceedings Workshop on Computer Vision, Representation and Control, Annapolis, 1984, pp. 164-169.
3. Ansaldi, S., De Floriani, L., Falcidieno, B., “An Edge-face Relational Scheme for Boundary Representations”, Computer Graphics Forum, 1985, to appear.
4. Baumgardt, B., “Winged-edge Polyhedron Representation”, Stanford Artificial Intelligence Report No. CS-320, 1972.
5. Berge, C., Graphes et Hypergraphes, Dunod, Paris, 1977.
6. Braid, I.C., Hillyard, R.C., Stroud, I.A., Stepwise Construction of Polyhedra in Geometric Modeling”, in: Mathematical Methods in Computer Graphics and Design, edited by K.W. Brodlie, Academic Press, 1980.
7. Hanranan, P.M.,rrCreating Volume Models from Edge-vertex Graphs”, Computer Graphics, 16, 3, 1982, pp. 77-84.
8. Harary, F., Graph Theory, Addison Wesley, Mass., 1969.
9. Mantyla, M., Sulonen, R., “GWB: a Solid Modeler with Euler Operators”, IEEE Computer Graphics and Applications, 1982, pp. 17-31.
10. Requicha, A.A.G., “Representation of Rigid Solids – Theory, Methods and Systems”, A.C.M. Computing Surveys, 12, 4, 1981, pp. $37-464~.
11. Weiler, K., “Edge-based Data Structures for Solid Modeling in Curved-Surface Environment”, IEEE Computer Graphics and Applications, 5, I, 1985, pp. 21-40.
12. Wilson, P.R., “Features”, CAM-I Interim Report III, October 1983.