“Fitting smooth surfaces to dense polygon meshes” by Krishnamurthy and Levoy

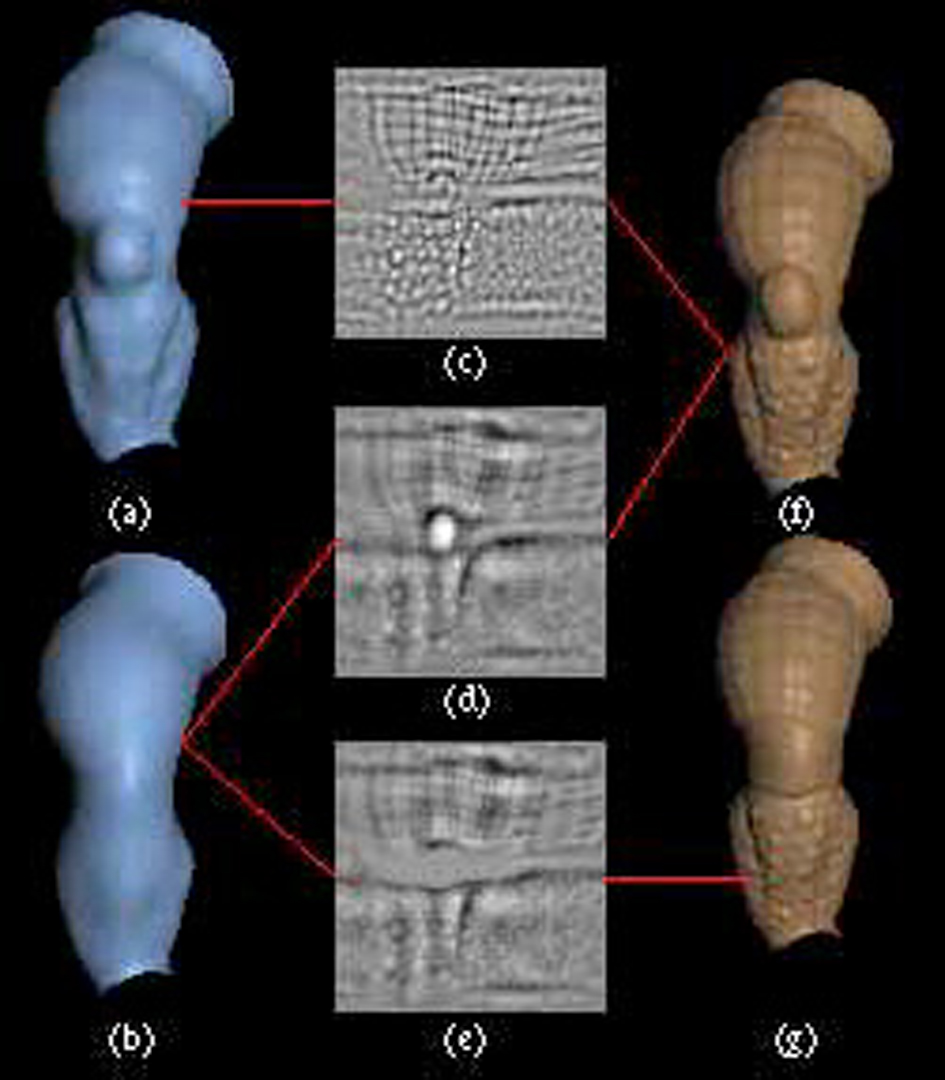
Recent progress in acquiring shape from range data permits the acquisition of seamless million-polygon meshes from physical models. In this paper, we present an algorithm and system for converting dense irregular polygon meshes of arbitrary topology into tensor product B-spline surface patches with accompanying displacement maps. This choice of representation yields a coarse but efficient model suitable for animation and a fine but more expensive model suitable for rendering. The first step in our process consists of interactively painting patch boundaries over a rendering of the mesh. In many applications, interactive placement of patch boundaries is considered part of the creative process and is not amenable to automation. The next step is gridded resampling of each bounded section of the mesh. Our resampling algorithm lays a grid of springs across the polygon mesh, then iterates between relaxing this grid and subdividing it. This grid provides a parameterization for the mesh section, which is initially unparameterized. Finally, we fit a tensor product B-spline surface to the grid. We also output a displacement map for each mesh section, which represents the error between our fitted surface and the spring grid. These displacement maps are images; hence this representation facilitates the use of image processing operators for manipulating the geometric detail of an object. They are also compatible with modern photo-realistic rendering systems. Our resampling and fitting steps are fast enough to surface a million polygon mesh in under 10 minutes – important for an interactive system.

1. A.V.Aho and J.D.Ullman. Data structures and algorithms. Addison-Wesley, 1979.
2. L Bardis and M Vafiadou. Ship-hull geometry representation with b-spline surface patches. Computer Aided Design, 24(4):217-222,1992.
3. Brian A. Barsky. End conditions and boundary conditions for uniform b-spline curve and surface representations. Computers In Industry, 3, 1982.
4. Richard Bartels, John Beatty, and Brian Barsky. An Int~vduction to Splinesfor Use in Computer Graphics and Geometric Modeling. Morgan Kaufmann Publishers, Palo Alto, CA, 1987.
5. James F. Blinn. Simulation of wrinkled surfaces. In Computer Graphics (SIG- GRAPH ’78 P1vceedings), volume 12, pages 286-292,1978.
6. J. Vezien Chakib Bennis and G. Iglesias. Piecewise surface flattening for nondistorted texture mapping. In Computer Graphics (SIGGRAPH’ 91 P~vceedings), volume 25, pages 237-246, July 1991.
7. Jindong Chen and Yijie Han. Shortest paths on a polyhedron. In P1vc. 6th Annual ACM Symposium on ComputationaI Geometry, pages 360-369, June 1990.
8. Robert L. Cook. Shade trees. In Computer Graphics (SIGGRAPH ’84 P1vceedings), volume 18, pages 223-231, July 1984.
9. Brian Curless and Marc Levoy. A volumetric method for building complex models from range images. In Computer Graphics (SIGGRAPH ’96 P1vceedings), August 1996.
10. Paul Dierckx. Curve and Sulface Fitting with Splines. Oxford Science Publications, New York, 1993.
11. Matthias Eck, Tony DeRose, Tom Duchamp, Hugues Hoppe, Michael Lounsbery, and Werner Stuetzle. Multiresolution analysis of arbitrary meshes. In Computer Graphics (P1vceedings of SIGGRAPH ’95), pages 173-182, August 1995.
12. Matthias Eck and Hugues Hoppe. Automatic reconstruction of b-spline surfaces of arbitrary topologicaltype. In Computer Graphics (P~vceedings of SIGGRAPH ‘ 96), August 1996.
13. Hugues Hoppe et al. Piecewise smooth surface reconstruction. In Computer Graphics (P1vceedings of SIGGRAPH ’94), pages 295-302, July 1994.
14. Gerald Farin. Curves and Sulfaces for Computer Aided Geometric Design. Academic Press, 1990.
15. David R. Forsey and Richard H. Bartels. Hierarchical B-spline refinement. In Computer Graphics (SIGGRAPH ’88 P1vceedings), volume 22, pages 205-212, August 1988.
16. Mark Halstead, Michael Kass, and Tony DeRose. Efficient, fair interpolation using Catmull-Clark surfaces. In Computer Graphics (SIGGRAPH ’93 P~vceedings), volume 27, pages 35-44, August 1993.
17. David Heeger and James R. Bergen. Pyramid-basedtexture analysis/synthesis. In Computer Graphics (SIGGRAPH ’95 P1vceedings), pages 229-237, July 1995.
18. J Hoschek and D Lasser. Fundamentals of Computer Aided Geometric Design. AK Peters, Wellesley, 1993.
19. Charles L. Lawson and Richard J. Hanson. Solving Least Square P1vblems. Prentice-Hall, Englewood Cliffs, New Jersey, 1974.
20. W. Ma and J P Kruth. Parameterization of randomly measured points for least squares fitting of b-spline curves and surfaces. Computer Aided Design, 27(9):663-675,1995.
21. Jerome Maillot. Interactive texture mapping. In Computer Graphics (SIGGRAPH ’93 P1vceedings), volume 27, pages 27-34, July 1993.
22. M.J. Milroy, C. Bradley, G. W. Vickers, and D. J. Weir. G1 continuity ofb-spline surface patches in reverse engineering. Computer-Aided Design, 27:471-478, 1995.
23. J.S.B. Mitchell, D. M. Mount, and C. H. Papadimitriou. The discrete geodesic problem. SIAM J. Comput., 16:647-668,1987.
24. Eben Ostby. Describing free-form 3d surfaces for animation. In Workshop on Interactive 3D Graphics, pages 251-258,1986.
25. Hans K. Pedersen. Decorating implicit surfaces. In Computer Graphics (P~vceedings of SIGGRAPH ’95), pages 291-300,August 1995.
26. Hans K. Pedersen. A framework for interactive texturing on curved surfaces. In Computer Graphics (P1vceedings of SIGGRAPH ’96), August 1996.
27. Jorg Peters. Fitting smooth parametric surfaces to 3D data. Ph.d. thesis, Univ. of Wisconsin-Madison, 1990.
28. William T. Reeves. Simple and complex facial animation: Case studies. In State Of The Art In FaciaI Animation, SIGGRAPH course 26, pages 90-106.1990.
29. David R.Forsey and Richard H. Bartels. Surface fitting with hierarchical splines. In Topics in the Construction, Manipulation, and Assessment of Spline Sulfaces, SIGGRAPH course 25, pages 7-0-7-14.1991.
30. D.F. Rogers and N. G. Fog. Constrained b-spline curve and surface fitting. Computer Aided Geometric Design, 21:641-648, December 1989.
31. Francis J. M. Schmitt, Brian A. Barsky, and Wen hui Du. An adaptive subdivision method for surface-fitting from sampled data. In Computer Graphics (SIG- GRAPH ’86 P1vceedings), volume 20, pages 179-188, August 1986.
32. Stan Sclaroff and Alex Pentland. Generalized implicit functions for computer graphics. In Computer Graphics (SIGGRAPH ’91 P1vceedings), volume 25, pages 247-250, July 1991.
33. Sarvajit S. Sinha and Pradeep Seneviratne. Single valuedness, parameterization and approximating 3d surfaces using b-splines. Geometric Methods in Computer Vision 2, pages 193-204,1993.
34. J.F. Thompson. The Eagle Papers. Mississippi State University, P.O. Drawer 6176, Mississippi State, MS 39762.
35. Greg Turk. Re-tiling polygonal surfaces. In Computer Graphics (SIGGRAPH ’92 P1vceedings), volume 26, pages 55-64, July 1992.
36. Greg Turk and Marc Levoy. Zippered polygon meshes from range images. In Computer Graphics (SIGGRAPH ‘ 94 P1vceedings), pages 311-318, July 1994.
37. William Welch and Andrew Witkin. Free-Form shape design using triangulated surfaces. In Computer Graphics (P1vceedings of SIGGRAPH ’94), pages 247- 256, July 1994.
38. William Welch and Andrew Witkin. Free-form shape design using triangulated surfaces. In Computer Graphics (SIGGRAPH ’94 P1vceedings), volume 28, pages 237-246, July 1994.