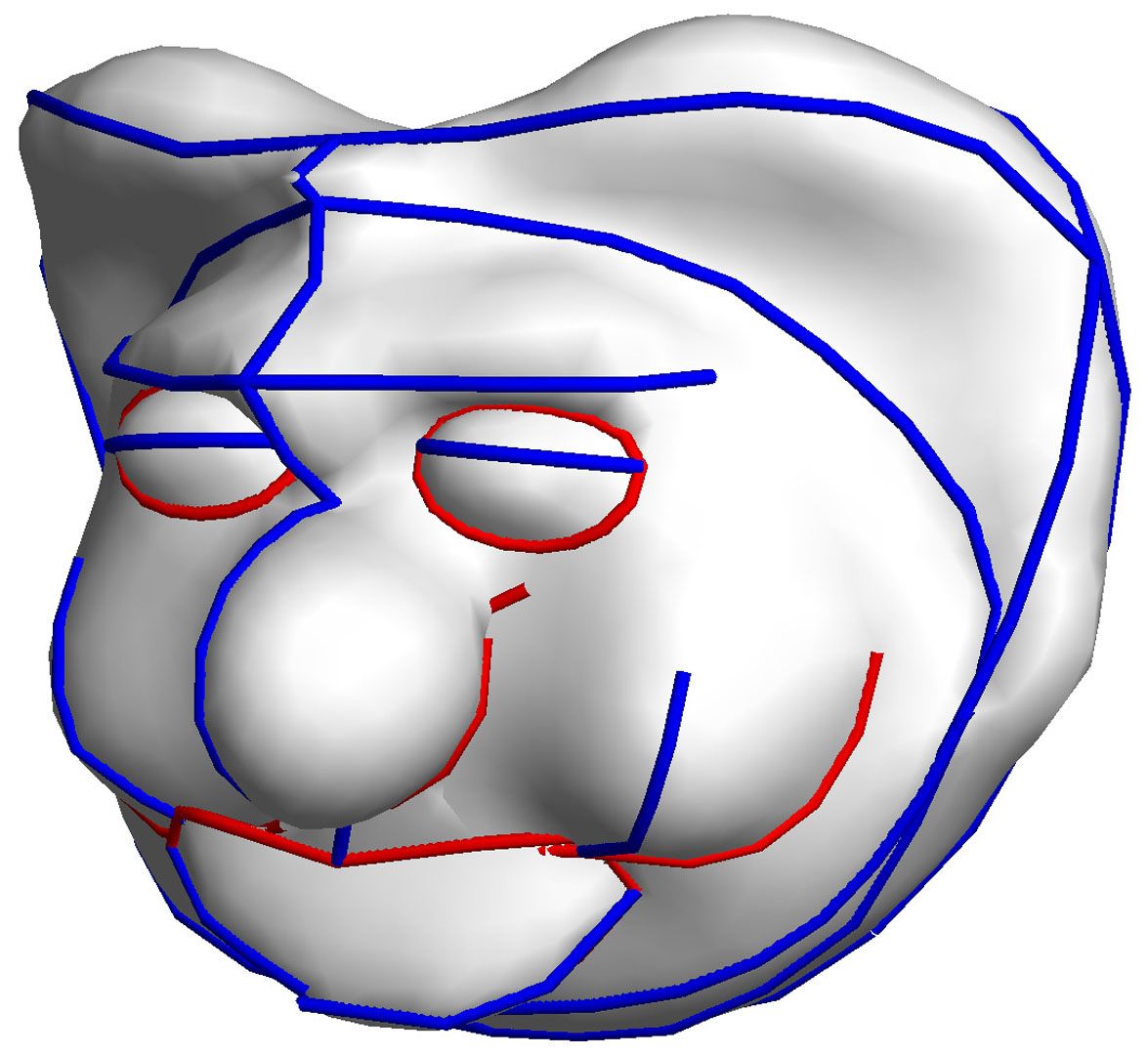
“FiberMesh: designing freeform surfaces with 3D curves” by Nealen, Igarashi, Sorkine-Hornung and Alexa

This paper presents a system for designing freeform surfaces with a collection of 3D curves. The user first creates a rough 3D model by using a sketching interface. Unlike previous sketching systems, the user-drawn strokes stay on the model surface and serve as handles for controlling the geometry. The user can add, remove, and deform these control curves easily, as if working with a 2D line drawing. The curves can have arbitrary topology; they need not be connected to each other. For a given set of curves, the system automatically constructs a smooth surface embedding by applying functional optimization. Our system provides real-time algorithms for both control curve deformation and the subsequent surface optimization. We show that one can create sophisticated models using this system, which have not yet been seen in previous sketching or functional optimization systems.

1. 3ds MAX, 2007. Autodesk, http://www.autodesk.com/3dsmax.Google Scholar
2. Allen, B., Curless, B., and Popović, Z. 2003. The space of human body shapes: reconstruction and parameterization from range scans. ACM Trans. Graph. 22, 3, 587–594. Google ScholarDigital Library
3. Angeldis, A., Cani, M.-P., Wyvill, G., and King, S. 2006. Swirling-sweepers: constant volume modeling. Grap. Models 68, 4, 324–332. Google ScholarDigital Library
4. Bobenko, A. I., and Schroeder, P. 2005. Discrete Willmore flow. In Eurographics Symposium on Geometry Processing, 101–110. Google ScholarDigital Library
5. Botsch, M., and Kobbelt, L. 2004. An intuitive framework for real-time freeform modeling. ACM Trans. Graph. 23, 3, 630–634. Google ScholarDigital Library
6. Botsch, M., and Sorkine, O. 2007. On linear variational surface deformation methods. IEEE Transactions on Visualization and Computer Graphics. To appear. Google ScholarDigital Library
7. Botsch, M., Pauly, M., and Gross, M. 2006. PriMo: coupled prisms for intuitive surface modeling. In Eurographics Symposium on Geometry Processing, 11–20. Google ScholarDigital Library
8. Davis, T. A. 2004. UMFPACK V4.3—an unsymmetric-pattern multifrontal method. ACM Trans. Math. Softw. 30, 2, 196–199. Google ScholarDigital Library
9. Felippa, C., 2007. Nonlinear finite element methods. www.colorado.edu/engineering/CAS/courses.d/NFEM.d/.Google Scholar
10. Fu, H., Au, O. K.-C., and Tai, C.-L. 2007. Effective derivation of similarity transformations for implicit Laplacian mesh editing. Computer Graphics Forum 21, 1, 34–45.Google ScholarCross Ref
11. Gingold, C., 2007. SPORE’s magic crayons. Game Developers Conference.Google Scholar
12. Huang, J., Shi, X., Liu, X., Zhou, K., Wei, L.-Y., Teng, S.-H., Bao, H., Guo, B., and Shum, H.-Y. 2006. Subspace gradient domain mesh deformation. ACM Trans. Graph. 25, 3, 1126–1134. Google ScholarDigital Library
13. Igarashi, T., and Hughes, J. F. 2003. Smooth meshes for sketch-based freeform modeling. In ACM Symposium on Interactive 3D Graphics, 139–142. Google ScholarDigital Library
14. Igarashi, T., Matsuoka, S., and Tanaka, H. 1999. Teddy: A sketching interface for 3D freeform design. In ACM SIGGRAPH, 409–416. Google ScholarDigital Library
15. Igarashi, T., Moscovich, T., and Hughes, J. F. 2005. Asrigid-as-possible shape manipulation. ACM Trans. Graph. 24, 3, 1134–1141. Google ScholarDigital Library
16. Kara, L. B., and Shimada, K. 2007. Sketch-based 3D shape creation for industrial styling design. IEEE Computer Graphics and Applications 27, 1, 60–71. Google ScholarDigital Library
17. Karpenko, O. A., and Hughes, J. F. 2006. SmoothSketch: 3D free-form shapes from complex sketches. ACM Trans. Graph. 25, 3, 589–598. Google ScholarDigital Library
18. Karpenko, O., Hughes, J. F., and Raskar, R. 2002. Free-form sketching with variational implicit surfaces. Computer Graphics Forum 21, 3, 585–594.Google ScholarCross Ref
19. Kobbelt, L., Campagna, S., Vorsatz, J., and Seidel, H.-P. 1998. Interactive multi-resolution modeling on arbitrary meshes. In ACM SIGGRAPH, 105–114. Google ScholarDigital Library
20. Lipman, Y., Sorkine, O., Levin, D., and Cohen-Or, D. 2005. Linear rotation-invariant coordinates for meshes. ACM Trans. Graph. 24, 3, 479–487. Google ScholarDigital Library
21. Markosian, L., Cohen, J. M., Crulli, T., and Hughes, J. 1999. Skin: a constructive approach to modeling free-form shapes. In ACM SIGGRAPH, 393–400. Google ScholarDigital Library
22. Maxis, 2007. SPORE#8482;. Electronic Arts, www.spore.com.Google Scholar
23. Maya, 2007. Autodesk, http://www.autodesk.com/maya.Google Scholar
24. Moreton, H. P., and Séquin, C. H. 1992. Functional optimization for fair surface design. In ACM SIGGRAPH, 167–176. Google ScholarDigital Library
25. Nealen, A., and Sorkine, O., 2007. A note on boundary constraints for linear variational surface design. Technical Report, TU Berlin.Google Scholar
26. Nealen, A., Sorkine, O., Alexa, M., and Cohen-Or, D. 2005. A sketch-based interface for detail-preserving mesh editing. ACM Trans. Graph. 24, 3, 1142–1147. Google ScholarDigital Library
27. Nealen, A., Igarashi, T., Sorkine, O., and Alexa, M. 2006. Laplacian mesh optimization. In ACM GRAPHITE, 381–389. Google ScholarDigital Library
28. Perry, R. N., and Frisken, S. F. 2001. Kizamu: a system for sculpting digital characters. In ACM SIGGRAPH, 47–56. Google ScholarDigital Library
29. Schaefer, S., Warren, J., and Zorin, D. 2005. Lofting curve networks with subdivision surfaces. In Symposium on Geometry Processing, 105–116. Google ScholarDigital Library
30. Schmidt, R., Wyvill, B., Sousa, M., and Jorge, J. 2005. ShapeShop: Sketch-based solid modeling with blobtrees. In Eurographics Workshop on Sketch-Based Interfaces and Modeling, 53–62.Google Scholar
31. Schneider, R., and Kobbelt, L. 2001. Geometric fairing of irregular meshes for free-form surface design. Computer Aided Geometric Design 18, 4, 359–379. Google ScholarDigital Library
32. Sederberg, T. W., Zheng, J., Bakenov, A., and Nasri, A. 2003. T-Splines and T-NURCCs. ACM Trans. Graph. 22, 3, 477–484. Google ScholarDigital Library
33. Singh, K., and Fiume, E. L. 1998. Wires: A geometric deformation technique. In ACM SIGGRAPH, 405–414. Google ScholarDigital Library
34. Sorkine, O., and Cohen-Or, D. 2004. Least-squares meshes. In Shape Modeling International, 191–199. Google ScholarCross Ref
35. Sorkine, O., Lipman, Y., Cohen-Or, D., Alexa, M., Rössl, C., and Seidel, H.-P. 2004. Laplacian surface editing. In Eurographics Symposium on Geometry Processing, 179–188. Google ScholarDigital Library
36. Sorkine, O. 2006. Differential representations for mesh processing. Computer Graphics Forum 25, 4, 789–807.Google ScholarCross Ref
37. Sumner, R., and Popović, J. 2004. Deformation transfer for triangle meshes. ACM Trans. Graph. 23, 3, 399–405. Google ScholarDigital Library
38. Surazhsky, V., and Gotsman, C. 2003. Explicit surface remeshing. In Eurographics Symposium on Geometry Processing, 20–30. Google ScholarDigital Library
39. Toledo, S. 2003. Taucs: A Library of Sparse Linear Solvers. Tel Aviv University.Google Scholar
40. Turk, G., and O’Brien, J. F. 2002. Modelling with implicit surfaces that interpolate. ACM Trans. Graph. 21, 4, 855–873. Google ScholarDigital Library
41. von Funck, W., Theisel, H., and Seidel, H.-P. 2006. Vector field based shape deformations. ACM Trans. Graph. 25, 3, 1118–1125. Google ScholarDigital Library
42. Wardetzky, M., Bergou, M., Harmon, D., Zorin, D., and Grinspun, E. 2007. Discrete quadratic curvature energies. CAGD (to appear). Google ScholarDigital Library
43. Welch, W., and Witkin, A. 1994. Free-form shape design using triangulated surfaces. In ACM SIGGRAPH, 247–256. Google ScholarDigital Library
44. Yu, Y., Zhou, K., Xu, D., Shi, X., Bao, H., Guo, B., and Shum, H.-Y. 2004. Mesh editing with Poisson-based gradient field manipulation. ACM Trans. Graph. 23, 3, 644–651. Google ScholarDigital Library
45. Zayer, R., Rössl, C., Karni, Z., and Seidel, H.-P. 2005. Harmonic guidance for surface deformation. Computer Graphics Forum 24, 3, 601–609.Google ScholarCross Ref
46. Zhou, K., Huang, J., Snyder, J., Liu, X., Bao, H., Guo, B., and Shum, H.-Y. 2005. Large mesh deformation using the volumetric graph Laplacian. ACM Trans. Graph, 24, 3, 496–503. Google ScholarDigital Library
47. Zorin, D., Schröder, P., and Sweldens, W. 1997. Interactive multiresolution mesh editing. In ACM SIGGRAPH, 259–268. Google ScholarDigital Library