“Feature-adaptive GPU rendering of Catmull-Clark subdivision surfaces” by Nießner, Loop, Meyer and DeRose

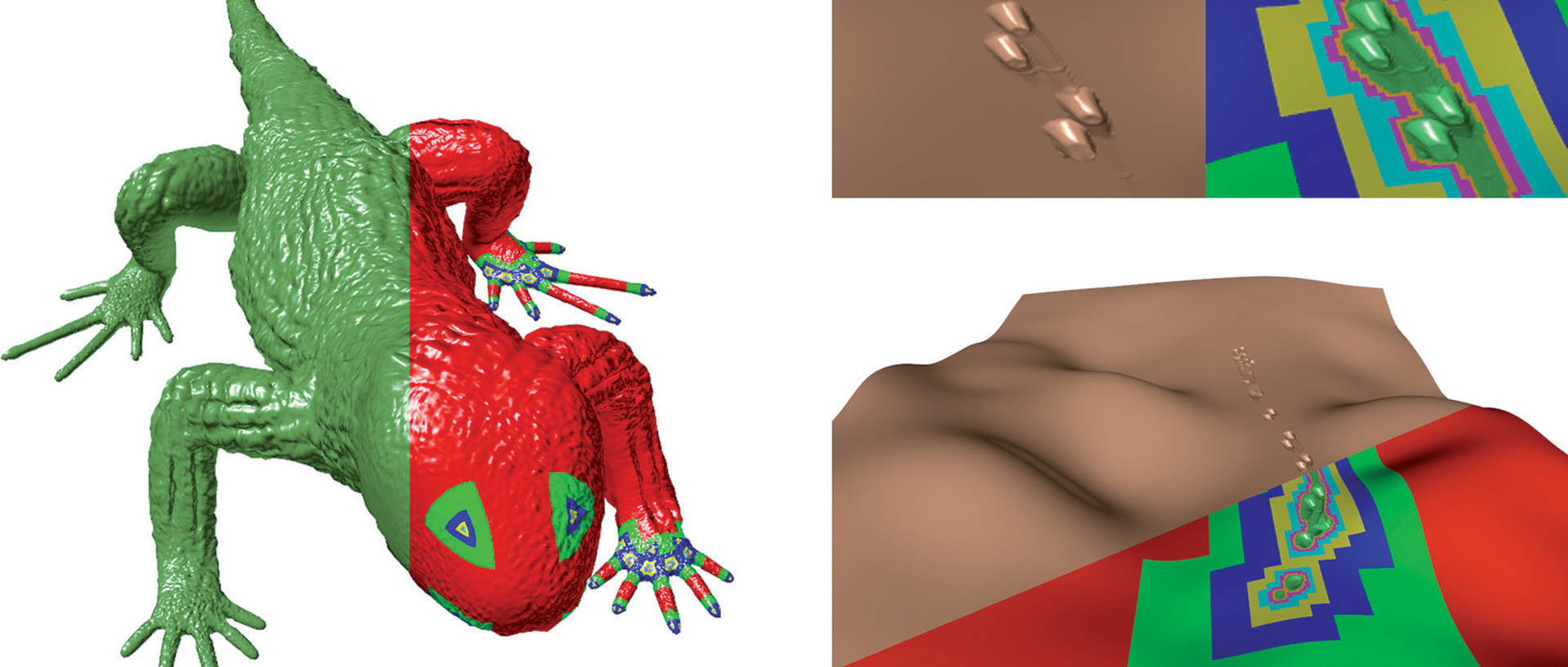
We present a novel method for high-performance GPU-based rendering of Catmull-Clark subdivision surfaces. Unlike previous methods, our algorithm computes the true limit surface up to machine precision, and is capable of rendering surfaces that conform to the full RenderMan specification for Catmull-Clark surfaces. Specifically, our algorithm can accommodate base meshes consisting of arbitrary valence vertices and faces, and the surface can contain any number and arrangement of semisharp creases and hierarchically defined detail. We also present a variant of the algorithm which guarantees watertight positions and normals, meaning that even displaced surfaces can be rendered in a crack-free manner. Finally, we describe a view-dependent level-of-detail scheme which adapts to both the depth of subdivision and the patch tessellation density. Though considerably more general, the performance of our algorithm is comparable to the best approximating method, and is considerably faster than Stam’s exact method.

Bolz, J. and Schröder, P. 2002. Rapid evaluation of catmull-clark subdivision surfaces. In Proceeding of the International Conference on 3D Web Technology. 11–17. Google ScholarDigital Library
Bunnell, M. 2005. Adaptive tessellation of subdivision surfaces with displacement mapping. In GPU Gems, 2. 109–122.Google Scholar
Castaño, I. 2008. Tessellation of subdivision surfaces in DirectX 11. Gamefest 2008. http://developer.nvidia.com/object/gamefest-2008-subdiv. html.Google Scholar
Catmull, E. 1974. Subdivision algorithms for the display of curved surfaces. Ph.D. thesis, The University of Utah. Google ScholarDigital Library
Catmull, E. and Clark, J. 1978. Recursively generated B-spline surfaces on arbitrary topological meshes. Comput.-Aid. Des. 10, 6, 350–355.Google ScholarCross Ref
Cook, R. L., Carpenter, L., and Catmull, E. 1987. The Reyes image rendering architecture. SIGGRAPH Comput. Graph. 21, 4, 95–102. Google ScholarDigital Library
DeRose, T., Kass, M., and Truong, T. 1998. Subdivision surfaces in character animation. In Proceedings of the Conference SIGGRAPH’98 85–94. Google ScholarDigital Library
Doo, D. and Sabin, M. 1978. Behaviour of recursive division surfaces near extraordinary points. Comput. Aid. Des. 10, 6, 356–360.Google ScholarCross Ref
Fisher, M., Fatahalian, K., Boulos, S., Akeley, K., Mark, W. R., and Hanrahan, P. 2009. Diagsplit: Parallel, crack-free, adaptive tessellation for micropolygon rendering. ACM Trans. Graph. 28, 5, 150:1–150:10. Google ScholarDigital Library
Forsey, D. R. and Bartels, R. H. 1988. Hierarchical b-spline refinement. SIGGRAPH Comput. Graph. 22, 4, 205–212. Google ScholarDigital Library
Halstead, M., Kass, M., and DeRose, T. 1993. Efficient, fair interpolation using catmull-clark surfaces. In Proceedings of the Conference SIGGRAPH’93. ACM, New York, 35–44. Google ScholarDigital Library
Hoppe, H., Derose, T., Duchamp, T., Halstead, M., Jin, H., Mcdonald, J., Schweitzer, J., and Stuetzle, W. 1994. Piecewise smooth surface reconstruction. In Proceedings of the Conference SIGGRAPH’94. 295–302. Google ScholarDigital Library
Kovacs, D., Mitchell, J., Drone, S., and Zorin, D. 2009. Real-Time creased approximate subdivision surfaces. In Proceedings of the Symposium on Interactive 3D Graphics. 155–160. Google ScholarDigital Library
Loop, C. and Schaefer, S. 2008. Approximating catmull-clark subdivision surfaces with bicubic patches. ACM Trans. Graph. 27, 1, 8:1–8:11. Google ScholarDigital Library
Loop, C., Schaefer, S., Ni, T., and no, I. C. 2009. Approximating subdivision surfaces with gregory patches for tessellation hardware. ACM Trans. Graph. 28, 5, 151:1–151:9. Google ScholarDigital Library
Microsoft Corporation. 2009. Direct3D 11 features. http://msdn. microsoft.com/en-us/library/ff476342(VS.85).aspx.Google Scholar
Moreton, H. 2001. Watertight tessellation using forward differencing. In Proceedings of the ACM SIGGRAPH/EUROGRAPHICS Workshop on Graphics Hardware (HWWS’01). ACM, New York, 25–32. Google ScholarDigital Library
Myles, A., Ni, T., and Peters, J. 2008a. Fast parallel construction of smooth surfaces from meshes with tri/quad/pent facets. Comput. Graph. Forum 27, 5, 1365–1372. Google ScholarDigital Library
Myles, A., Yeo, Y. I., and Peters, J. 2008b. Gpu conversion of quad meshes to smooth surfaces. In Proceedings of the ACM Symposium on Solid and Physical Modeling (SPM’08). 321–326. Google ScholarDigital Library
Nasri, A. H. 1987. Polyhedral subdivision methods for free-form surfaces. ACM Trans. Graph. 6, 1, 29–73. Google ScholarDigital Library
Ni, T., Yeo, Y. I., Myles, A., Goel, V., and Peters, J. 2008. Gpu smoothing of quad meshes. In Proceedings of the IEEE International Conference on Shape Modeling and Applications (SMI’08). 3–9.Google Scholar
Patney, A., Ebeida, M. S., and Owens, J. D. 2009. Parallel view-dependent tessellation of catmull-clark subdivision surfaces. In Proceedings of the Conference on High Performance Graphics (HPG’09). ACM, New York, 99–108. Google ScholarDigital Library
Pixar Animation Studios. 2005. The RenderMan interface version 3.2.1. https://renderman.pixar.com/products/rispec/index.htm.Google Scholar
Sederberg, T., Cardon, D., Finnigan, G., North, N., Zheng, J., and Lyche, T. 2004. T-Spline simplification and local refinement. SIGGRAPH Comput. Graph. 23, 4, 276–283. Google ScholarDigital Library
Shiue, L.-J., Jones, I., and Peters, J. 2005. A realtime gpu subdivision kernel. ACM Trans. Graph. 24, 3, 1010–1015. Google ScholarDigital Library
Stam, J. 1998. Exact evaluation of Catmull-Clark subdivision surfaces at arbitrary parameter values. Comput. Graph. 32, 395–404. Google ScholarDigital Library
Von Herzen, B. and Barr, A. H. 1987. Accurate triangulations of deformed, intersecting surfaces. In Proceedings of the Conference SIGGRAPH’87. ACM, New York, 103–110. Google ScholarDigital Library