“Fast computation of shadow boundaries using spatial coherence and backprojections” by Stewart and Ghali

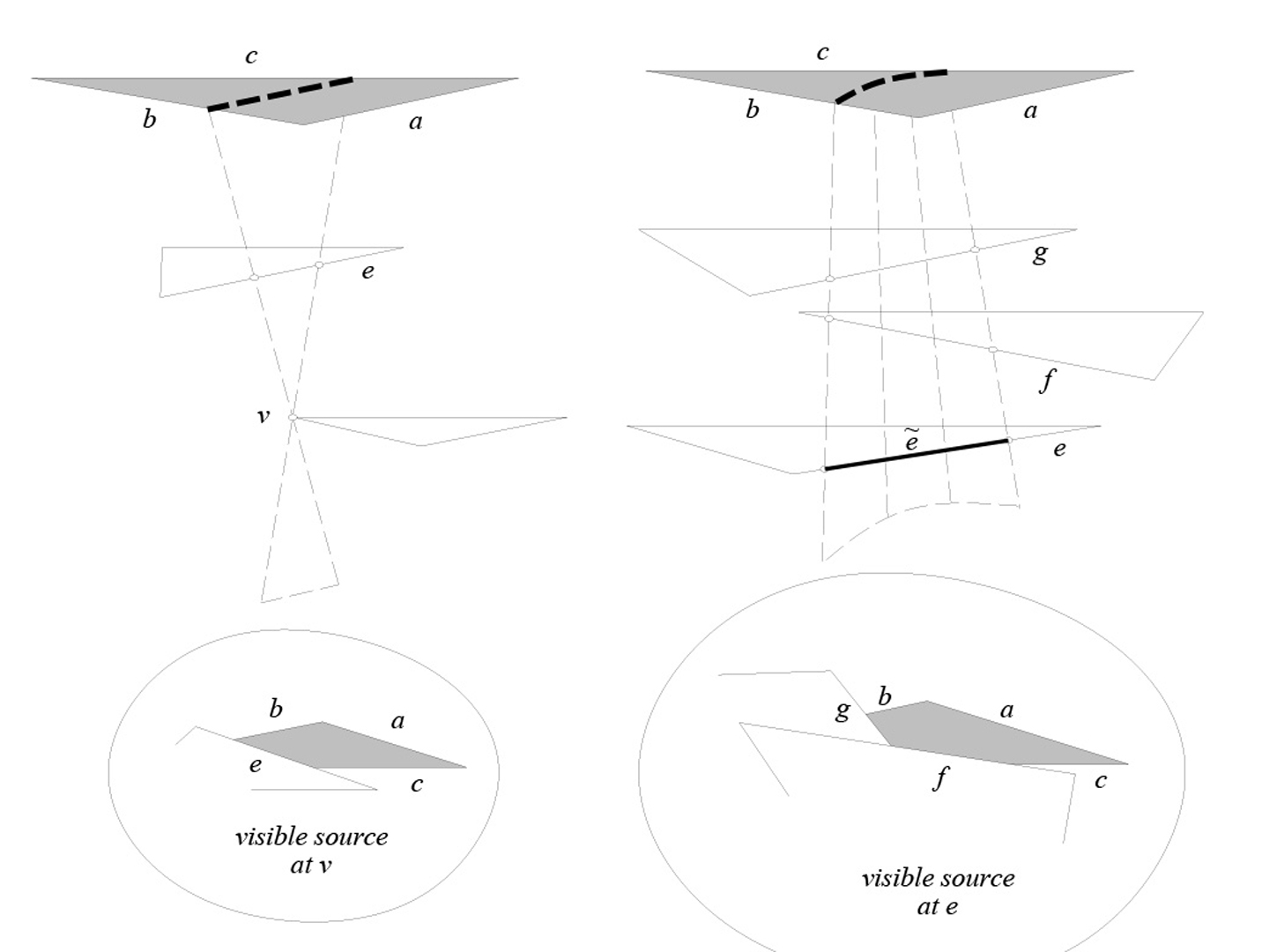
This paper describes a fast, practical algorithm to compute the shadow boundaries in a polyhedral scene illuminated by a polygonal light source. The shadow boundaries divide the faces of the scene into regions such that the structure or “aspect” of the visible area of the light source is constant within each region. The paper also describes a fast, practical algorithm to compute the structure of the visible light source in each region. Both algorithms exploit spatial coherence and are the most efficient yet developed.Given the structure of the visible light source in a region, queries of the form “What specific areas of the light source are visible?” can be answered almost instantly from any point in the region. This speeds up by several orders of magnitude the accurate computation of first level diffuse reflections due to an area light source. Furthermore, the shadow boundaries form a good initial decomposition of the scene for global illumination computations.

1. A. T. Campbell III and Donald Fussell. Adaptivemesh generationfor globaldiffuse illumination. Computer Graphics (SIGGRAPH ’90 Proceedings), 24(4):155-164, August 1990.
2. A. T. Campbell III and Donald Fussell. An analytic approach to illumination with area light sources. Department of Computer Sciences, University of Texas at Austin, technical report TR-91-25, August 1991.
3. Bernard Chazelle, Herbert Edelsbrunner, Leonidas Guibas, Micha Sharir, and Jorge Stolfi. Lines in space: Combinatorics and algorithms. New York University, Courant Inst. of Math. Sc. Technical Report No. 491, (also in STOC 1989, pp. 382-393), February 1990.
4. Norman Chin and Steven Feiner. Near real-time shadow generationusing bsp trees. Computer Graphics (SIGGRAPH ’89 Proceedings), 23(3):99-106, July 1989.
5. Michael Cohen, ShenchangEric Chen, John R. Wallace, and Donald P. Greenberg. A progressive refinement approach to fast radiosity image generation. Computer Graphics (SIGGRAPH ’88 Proceedings), 22(4):75-84, August 1988.
6. Michael Cohen and Donald P. Greenberg. The hemi-cube: A radiosity solution for complex environments. Computer Graphics (SIGGRAPH ’85 Proceedings), 19(3):31-40, August 1985.
7. Franklin C. Crow. Shadow algorithms for computer graphics. Computer Graphics (SIGGRAPH ’77 Proceedings), 11(2):242-248, July 1977.
8. George Drettakis. Structured Sampling and Reconstruction of Illumination for Image Synthesis. PhD thesis, University of Toronto, January 1994.
9. George Drettakis and Eugene Fiume. A fast shadow algorithm for area light sources using backprojections. COMPUTER GRAPHICS Proceedings, Annual Conference Series 1994, August 1994.
10. Herbert Edelsbrunner. Algorithms in Computational Geometry. Springer-Verlag, 1987.
11. Ziv Gigus, John Canny, and Raimund Seidel. Efficiently computingand represent-ing aspect graphs for polyhedral objects. IEEE Transactions on Pattern Analysis and Machine Intelligence, 13(6):542-551, June 1991.
12. Ziv Gigus and Jitendra Malik. Computing the aspect graphs for line drawings of polyhedral objects. IEEE Transactions on Pattern Analysis and Machine Intelli-gence, 12(2):113-122, February 1990.
13. Pat Hanrahan, David Salzman, and Larry Auperle. A rapid hierarchical radiosity algorithm. Computer Graphics (SIGGRAPH ’91 Proceedings), 25(4):197-206, July 1991.
14. Paul Heckbert. Discontinuitymeshing for radiosity. Third EurographicsWorkshop on Rendering, pages 203-215, May 1992.
15. Dani Lischinski, Filippo Tampieri, and Donald Greenberg. Discontinuity meshing for accurate radiosity. IEEE Computer Graphics & Applications, pages 25-39, November 1992.
16. Dani Lischinski, Filippo Tampieri, and Donald Greenberg. Combining hierarchi-cal radiosity and discontinuity meshing. COMPUTER GRAPHICS Proceedings, Annual Conference Series 1993, pages 199-208, August 1993.
17. M. McKenna. Worst-case optimal hidden-surface removal. ACM Trans. Graph., 6:19-28, 1987.
18. Ketan Mulmuley. An efficient algorithm for hidden surface removal. Computer Graphics (SIGGRAPH ’89 Proceedings), 23(3):379-388, July 1989.
19. TomoyukiNishita and Eihachiro Nakamae. Half-tone representation of 3-d objects illuminated by area sources or polyhedron sources. COMPSAC’83, Proc. IEEE 7th Intl. Conf. Soft. and Appl. Conf., pages 237-242, November 1983.
20. George Salmon. A treatise on the Analytical Geometry of Three Dimensions. Longmans, Green and Co., 1912.
21. Arthur Scherk. personal communications.
22. Duncan M. Y. Sommerville. Analytical Geometry in three dimensions. Cambridge University Press, 1934.
23. A. James Stewart and Sherif Ghali. An output sensitive algorithm for the computa-tion of shadow boundaries. In Canadian Conference on ComputationalGeometry, pages 291-296, August 1993.
24. Jorge Stolfi. Oriented Projective Geometry. PhD thesis, StanfordUniversity, 1988.
25. Seth Teller. Computingthe antipenumbraof polyhedralholes. Computer Graphics (SIGGRAPH Procedings), August 1992.
26. Seth Jared Teller. Visibility Computations in Densely Occluded Polyhedral Envi-ronments. PhD thesis, University of California at Berkeley, 1993.
27. Oswald Veblen and Wesley Young. Projective Geometry. Blaisdell Publishing Co., 1938.