“Expansion Cones: A Progressive Volumetric Mapping Framework” by Zenon Nigolian, Campen and Bommes
Conference:
Type(s):
Title:
- Expansion Cones: A Progressive Volumetric Mapping Framework
Session/Category Title: Marvelous Mappings
Presenter(s)/Author(s):
Moderator(s):
Abstract:
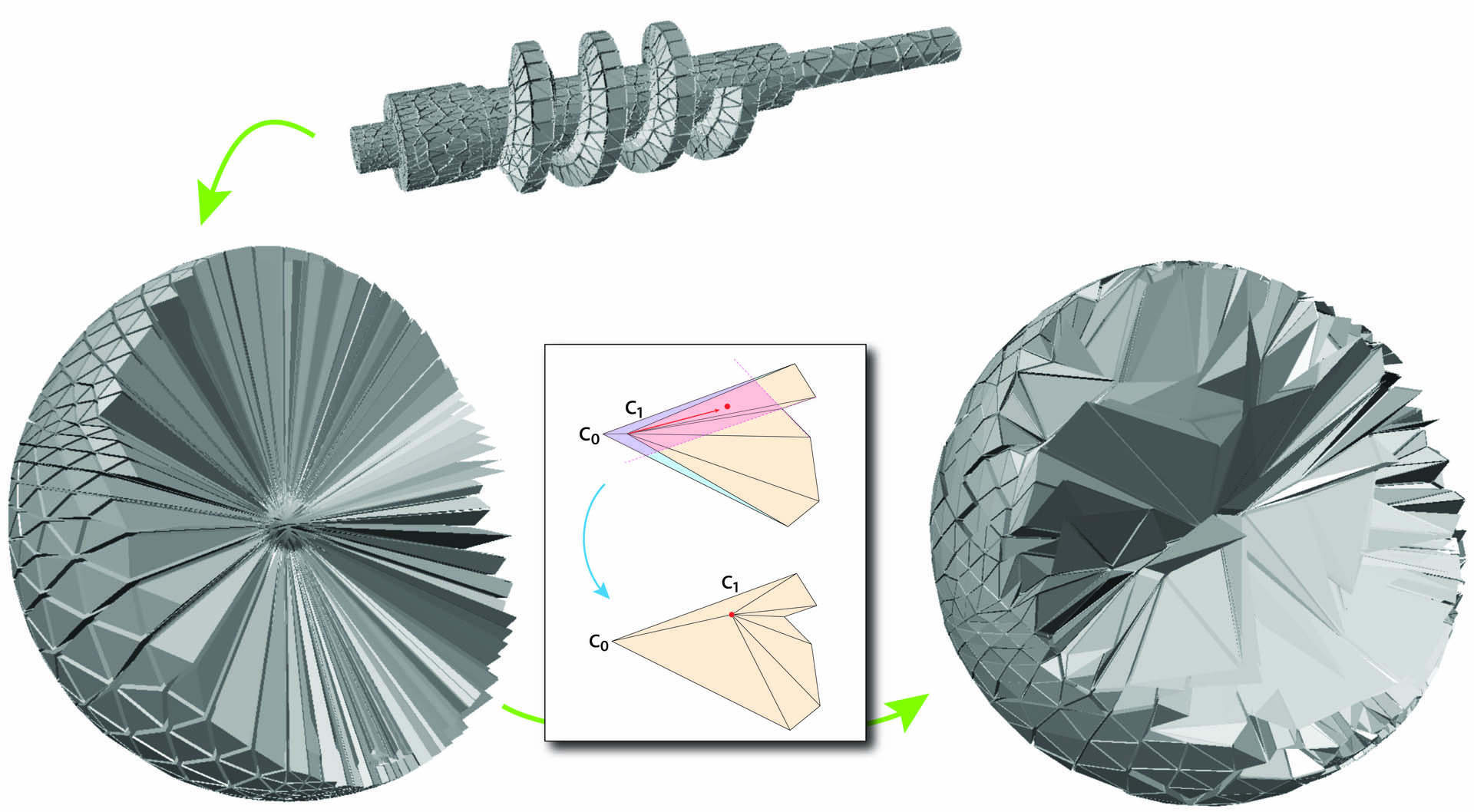
Volumetric mapping is a ubiquitous and difficult problem in Geometry Processing and has been the subject of research in numerous and various directions. While several methods show encouraging results, the field still lacks a general approach with guarantees regarding map bijectivity. Through this work, we aim at opening the door to a new family of methods by providing a novel framework based on the concept of progressive expansion. Starting from an initial map of a tetrahedral mesh whose image may contain degeneracies but no inversions, we incrementally adjust vertex images to expand degenerate elements. By restricting movement to so-called expansion cones, it is done in such a way that the number of degenerate elements decreases in a strictly monotonic manner, without ever introducing any inversion. Adaptive local refinement of the mesh is performed to facilitate this process. We describe a prototype algorithm in the realm of this framework for the computation of maps from ball-topology tetrahedral meshes to convex or star-shaped domains. This algorithm is evaluated and compared to state-of-the-art methods, demonstrating its benefits in terms of bijectivity. We also discuss the associated cost in terms of sometimes significant mesh refinement to obtain the necessary degrees of freedom required for establishing a valid mapping. Our conclusions include that while this algorithm is only of limited immediate practical utility due to efficiency concerns, the general framework has the potential to inspire a range of novel methods improving on the efficiency aspect.
References:
1. Karim Adiprasito and Bruno Benedetti. 2020. Barycentric Subdivisions of Convex Complexes Are Collapsible. Discrete Comput. Geom. 64, 3 (2020), 608–626.
2. Noam Aigerman and Yaron Lipman. 2013. Injective and Bounded Distortion Mappings in 3D. ACM Trans. Graph. 32, 4 (2013).
3. Noam Aigerman and Yaron Lipman. 2015. Orbifold Tutte Embeddings. ACM Trans. Graph. 34, 6 (2015).
4. Marc Alexa. 2023. Tutte Embeddings of Tetrahedral Meshes. Discrete & Computational Geometry (2023).
5. Anthony Anderson, Xiaoming Zheng, and Vittorio Cristini. 2005. Adaptive unstructured volume remeshing – I: The method. J. Comput. Phys. 208, 2 (2005), 616–625.
6. David Bommes, Marcel Campen, Hans-Christian Ebke, Pierre Alliez, and Leif Kobbelt. 2013. Integer-grid maps for reliable quad meshing. ACM Trans. Graph. 32, 4 (2013), 1–12.
7. Marcel Campen, Ryan Capouellez, Hanxiao Shen, Leyi Zhu, Daniele Panozzo, and Denis Zorin. 2021. Efficient and robust discrete conformal equivalence with boundary. ACM Trans. Graph. 40, 6 (2021), 1–16.
8. Marcel Campen, Cláudio T. Silva, and Denis Zorin. 2016. Bijective Maps from Simplicial Foliations. ACM Trans. Graph. 35, 4 (2016).
9. Tamal Dey, Herbert Edelsbrunner, Sumanta Guha, and Dmitry Nekhayev. 1999. Topology Preserving Edge Contraction. Publications de l’Institut Mathématique 66 (1999), 23–45.
10. Xingyi Du, Noam Aigerman, Qingnan Zhou, Shahar Z. Kovalsky, Yajie Yan, Danny M. Kaufman, and Tao Ju. 2020. Lifting Simplices to Find Injectivity. ACM Trans. Graph. 39, 4 (2020).
11. Andreas Fabri and Sylvain Pion. 2009. CGAL: The Computational Geometry Algorithms Library. In Proceedings of the 17th ACM SIGSPATIAL International Conference on Advances in Geographic Information Systems (GIS ’09).
12. Michael Floater and Valérie Pham-Trong. 2006. Convex combination maps over triangulations, tilings, and tetrahedral meshes. Adv. Comput. Math. 25 (2006), 347–356.
13. Michael S. Floater. 1997. Parametrization and smooth approximation of surface triangulations. Computer Aided Geometric Design 14, 3 (1997), 231–250.
14. Michael S. Floater. 2003. One-to-One Piecewise Linear Mappings over Triangulations. Math. Comput. 72, 242 (2003), 685–696.
15. Xiao-Ming Fu, Yang Liu, and Baining Guo. 2015. Computing Locally Injective Mappings by Advanced MIPS. ACM Trans. Graph. 34, 4 (2015).
16. Vladimir Garanzha, Igor Kaporin, Liudmila Kudryavtseva, François Protais, Nicolas Ray, and Dmitry Sokolov. 2021. Foldover-Free Maps in 50 Lines of Code. ACM Trans. Graph. 40, 4 (2021).
17. Mark Gillespie, Boris Springborn, and Keenan Crane. 2021. Discrete conformal equivalence of polyhedral surfaces. ACM Trans. Graph. 40, 4 (2021).
18. G. Hansen, Irmina Herburt, H. Martini, and M. Moszyńska. 2020. Starshaped sets. Aequationes mathematicae 94 (2020).
19. Steffen Hinderink and Marcel Campen. 2023. Galaxy Maps: Localized Foliations for Bijective Volumetric Mapping. ACM Trans. Graph. 42, 4 (2023).
20. K. Hormann and G. Greiner. 2000. MIPS: An Efficient Global Parametrization Method. In Curve and Surface Design 1999. 153–162.
21. Yixin Hu, Qingnan Zhou, Xifeng Gao, Alec Jacobson, Denis Zorin, and Daniele Panozzo. 2018. Tetrahedral Meshing in the Wild. ACM Trans. Graph. 37, 4 (2018).
22. Y. Jin, J. Huang, and R. Tong. 2014. Remeshing-Assisted Optimization for Locally Injective Mappings. Computer Graphics Forum 33, 5 (2014).
23. Vladislav Kraevoy and Alla Sheffer. 2004. Cross-parameterization and compatible remeshing of 3D models. ACM Trans. Graph. 23, 3 (2004), 861–869.
24. Vladislav Kraevoy, Alla Sheffer, and Craig Gotsman. 2003. Matchmaker: constructing constrained texture maps. ACM Trans. Graph. 22, 3 (2003).
25. Tong-Yee Lee, Shao-Wei Yen, and I-Cheng Yeh. 2008. Texture mapping with hard constraints using warping scheme. IEEE Transactions on Visualization and Computer Graphics 14, 2 (2008), 382–395.
26. Wentao Liao, Renjie Chen, Yuchen Hua, Ligang Liu, and Ofir Weber. 2021. Real-Time Locally Injective Volumetric Deformation. ACM Trans. Graph. 40, 4 (2021).
27. Yaron Lipman. 2012. Bounded distortion mapping spaces for triangular meshes. ACM Trans. Graph. 31, 4 (2012), 1–13.
28. Marco Livesu. 2020. A Mesh Generation Perspective on Robust Mappings. In Smart Tools and Apps for Graphics – Eurographics Italian Chapter Conference, Silvia Biasotti, Ruggero Pintus, and Stefano Berretti (Eds.).
29. Rahul Narain, Armin Samii, and James F. O’Brien. 2012. Adaptive Anisotropic Remeshing for Cloth Simulation. ACM Trans. Graph. 31, 6 (2012).
30. Michael Rabinovich, Roi Poranne, Daniele Panozzo, and Olga Sorkine-Hornung. 2017. Scalable locally injective mappings. ACM Trans. Graph. 36, 4 (2017).
31. Patrick Schmidt, Janis Born, Marcel Campen, and Leif Kobbelt. 2019. Distortion-Minimizing Injective Maps between Surfaces. ACM Trans. Graph. 38, 6 (2019).
32. Patrick Schmidt, Marcel Campen, Janis Born, and Leif Kobbelt. 2020. Inter-surface maps via constant-curvature metrics. ACM Trans. Graph. 39, 4 (2020), 119–1.
33. John Schreiner, Arul Asirvatham, Emil Praun, and Hugues Hoppe. 2004. Inter-surface mapping. In ACM SIGGRAPH 2004 Papers. 870–877.
34. Christian Schüller, Ladislav Kavan, Daniele Panozzo, and Olga Sorkine-Hornung. 2013. Locally Injective Mappings. In Proc. SGP ’13. 125–135.
35. Alla Sheffer, Emil Praun, and Kenneth Rose. 2006. Mesh parameterization methods and their applications. Foundations and Trends in Computer Graphics and Vision 2, 2 (2006), 105–171.
36. Hanxiao Shen, Zhongshi Jiang, Denis Zorin, and Daniele Panozzo. 2019. Progressive Embedding. ACM Trans. Graph. 38, 4 (2019).
37. Jason Smith and Scott Schaefer. 2015. Bijective Parameterization with Free Boundaries. ACM Trans. Graph. 34, 4 (2015), 70:1–70:9.
38. Jian-Ping Su, Xiao-Ming Fu, and Ligang Liu. 2019. Practical foldover-free volumetric mapping construction. Computer Graphics Forum 38, 7 (2019), 287–297.
39. William T. Tutte. 1963. How to Draw a Graph. Proceedings of The London Mathematical Society 13 (1963), 743–767.
40. Ofir Weber and Denis Zorin. 2014. Locally Injective Parametrization with Arbitrary Fixed Boundaries. ACM Trans. Graph. 33, 4 (2014).
41. Martin Wicke, Daniel Ritchie, Bryan M Klingner, Sebastian Burke, Jonathan R Shewchuk, and James F O’Brien. 2010. Dynamic local remeshing for elastoplastic simulation. ACM Trans. Graph. 29, 4 (2010), 1–11.
42. Jiazhi Xia, Ying He, Shuchu Han, Chi-Wing Fu, Feng Luo, and Xianfeng Gu. 2010. Parameterization of Star-Shaped Volumes Using Green’s Functions. In Advances in Geometric Modeling and Processing. Springer, Berlin, Heidelberg, 219–235.