“Exact evaluation of Catmull-Clark subdivision surfaces at arbitrary parameter values” by Stam

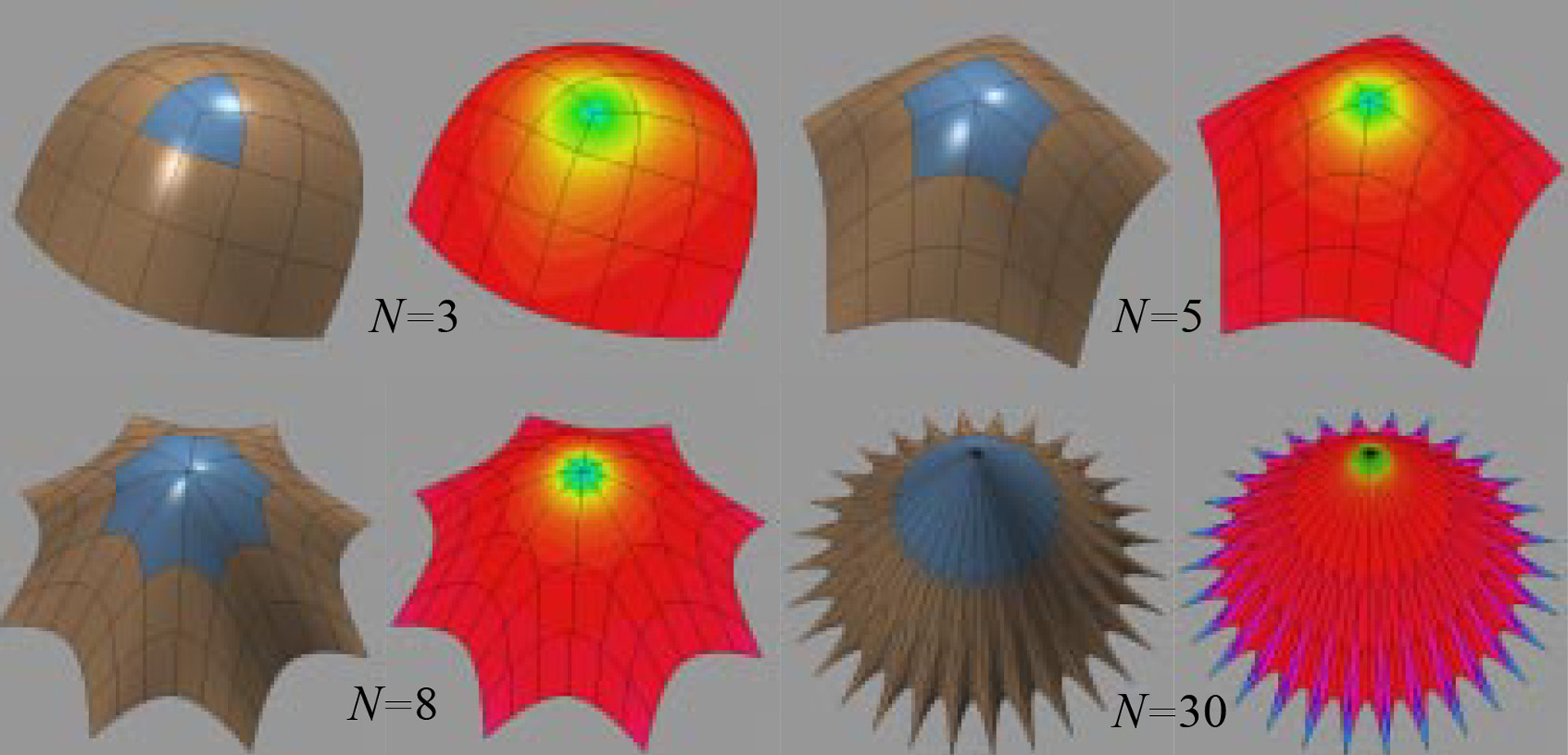
In this paper we disprove the belief widespread within the computer graphics community that Catmull-Clark subdivision surfaces cannot be evaluated directly without explicitly subdividing. We show that the surface and all its derivatives can be evaluated in terms of a set of eigenbasis functions which depend only on the subdivision scheme and we derive analytical expressions for these basis functions. In particular, on the regular part of the control mesh where Catmull-Clark surfaces are bi-cubic B-splines, the eigenbasis is equal to the power basis. Also, our technique is both easy to implement and efficient. We have used our implementation to compute high quality curvature plots of subdivision surfaces. The cost of our evaluation scheme is comparable to that of a bi-cubic spline. Therefore, our method allows many algorithms developed for parametric surfaces to be applied to Catmull-Clark subdivision surfaces. This makes subdivision surfaces an even more attractive tool for free-form surface modeling.

1. A. A. Ball and J. Y. Storry. Conditions For Tangent Plane Continuity Over Recursively Defined B-spline Surfaces. ACM Transactions on Graphics, 7(2):83-102, April 1988.
2. E. Catmull and J. Clark. Recursively Generated B-Spline Surfaces On Arbitrary Topological Meshes. Computer Aided Design, 10(6):350-355, 1978.
3. D. Doo and M. A. Sabin. Behaviour Of Recursive Subdivision Surfaces Near Extraordinary Points. Computer Aided Design, 10(6):356-360, 1978.
4. M. Halstead, M. Kass, and T. DeRose. Efficient, Fair Interpolation Using Catmull-Clark Surfaces. In Proceedings of SIG- GRAPH ’93, pages 35-44. Addison-Wesley Publishing Company, August 1993.
5. C.T. Loop. Smooth Subdivision Smfaces Based on Triangles. M.S. Thesis, Department of Mathematics, University of Utah, August 1987.
6. J. Peters and U. Reif. Analysis Of Generalized B-Splines Subdivision Algorithms. To appear in SIAM Journal of Numerical Analysis.
7. U. Reif. A Unified Approach To Subdivision Algorithms Near Extraordinary Vertices. Computer Aided Geometric Design, 12:153-174, 1995.
8. J. Stare. Evaluation Of Loop Subdivision Surfaces. SIG- GRAPH’98 CDROM Proceedings, 1998.
9. J. Warren. Subdivision Methods For Geometric Design. Unpublished manuscript. Preprint available on the web at http://www, cs. rice. edu/- jwarren/papers/book, ps. gz.
10. D. N. Zorin. Subdivision and Multiresolution Smface Representations. PhD thesis, Caltech, Pasadena, California, 1997.