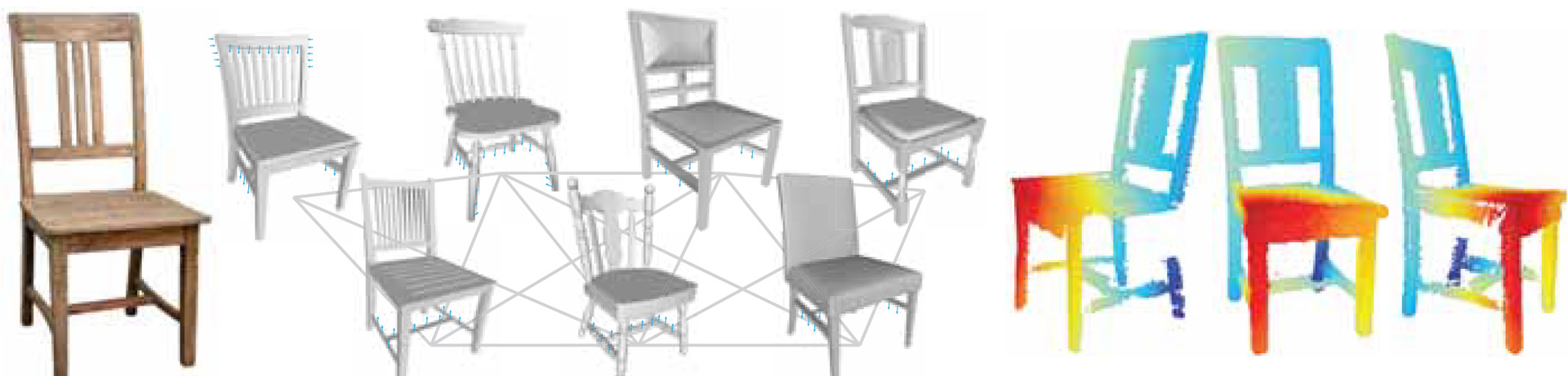
“Estimating image depth using shape collections” by Su, Huang, Mitra, Li and Guibas
Conference:
Type(s):
Title:
- Estimating image depth using shape collections
Session/Category Title:
- Shape Collection
Presenter(s)/Author(s):
Moderator(s):
Abstract:
Images, while easy to acquire, view, publish, and share, they lack critical depth information. This poses a serious bottleneck for many image manipulation, editing, and retrieval tasks. In this paper we consider the problem of adding depth to an image of an object, effectively ‘lifting’ it back to 3D, by exploiting a collection of aligned 3D models of related objects. Our key insight is that, even when the imaged object is not contained in the shape collection, the network of shapes implicitly characterizes a shape-specific deformation subspace that regularizes the problem and enables robust diffusion of depth information from the shape collection to the input image. We evaluate our fully automatic approach on diverse and challenging input images, validate the results against Kinect depth readings, and demonstrate several imaging applications including depth-enhanced image editing and image relighting.
References:
1. Averkiou, M., Kim, V., Zheng, Y., and Mitra, N. J. 2014. Shapesynth: Parameterizing model collections for coupled shape exploration and synthesis. CGF.Google Scholar
2. Chaudhuri, S., Kalogerakis, E., Guibas, L., and Koltun, V. 2011. Probabilistic reasoning for assembly-based 3d modeling. ACM ToG 30, 4 (Aug.), 35:1–35:10. Google ScholarDigital Library
3. Chen, D.-Y., Tian, X.-P., Shen, Y.-T., and Ouhyoung, M. 2003. On visual similarity based 3d model retrieval. CGF 22, 3, 223–232.Google ScholarCross Ref
4. Coifman, R. R., Lafon, S., Lee, A. B., Maggioni, M., Nadler, B., Warner, F., and Zucker, S. W. 2005. Geometric diffusions as a tool for harmonic analysis and structure definition of data: Diffusion maps. PNAS 102, 21, 7426–7431.Google ScholarCross Ref
5. Cyr, C. M., and Kimia, B. B. 2004. A similarity-based aspect-graph approach to 3d object recognition. IJCV 57, 1 (Apr.), 5–22. Google ScholarDigital Library
6. Dalal, N., and Triggs, B. 2005. Histograms of oriented gradients for human detection. In Proc. CVPR, 886–893. Google ScholarDigital Library
7. Funkhouser, T., Kazhdan, M., Shilane, P., Min, P., Kiefer, W., Tal, A., Rusinkiewicz, S., and Dobkin, D. 2004. Modeling by example. ACM ToG 23, 3 (Aug.), 652–663. Google ScholarDigital Library
8. Goldman, D. B., Curless, B., Hertzmann, A., and Seitz, S. M. 2005. Shape and spatially-varying brdfs from photometric stereo. In Proc. ICCV, 341–348. Google ScholarDigital Library
9. Hoiem, D., Efros, A. A., and Hebert, M. 2005. Automatic photo pop-up. ACM ToG 24, 3 (July), 577–584. Google ScholarDigital Library
10. Huang, Q., and Guibas, L. 2013. Consistent shape maps via semidefinite programming. CGF 32, 5, 177–186. Google ScholarDigital Library
11. Huang, Q., Koltun, V., and Guibas, L. 2011. Joint shape segmentation using linear programming. ACM ToG 30, 6. Google ScholarDigital Library
12. Huang, Q.-X., Su, H., and Guibas, L. 2013. Fine-grained semi-supervised labeling of large shape collections. ACM ToG 32, 6 (Nov.), 190:1–190:10. Google ScholarDigital Library
13. Kalogerakis, E., Chaudhuri, S., Koller, D., and Koltun, V. 2012. A probabilistic model for component-based shape synthesis. ACM ToG 31, 4 (July), 55:1–55:11. Google ScholarDigital Library
14. Kazhdan, M., Bolitho, M., and Hoppe, H. 2006. Poisson surface reconstruction. CGF, 61–70. Google ScholarDigital Library
15. Kim, V. G., Li, W., Mitra, N. J., DiVerdi, S., and Funkhouser, T. 2012. Exploring collections of 3d models using fuzzy correspondences. ACM ToG 31, 4 (July), 54:1–54:11. Google ScholarDigital Library
16. Kim, Y. M., Mitra, N. J., Yan, D.-M., and Guibas, L. 2012. Acquiring 3d indoor environments with variability and repetition. ACM ToG 31, 6 (Nov.), 138:1–138:11. Google ScholarDigital Library
17. Kim, V. G., Li, W., Mitra, N. J., Chaudhuri, S., DiVerdi, S., and Funkhouser, T. 2013. Learning part-based templates from large collections of 3d shapes. ACM ToG 32, 4, 70:1–70:12. Google ScholarDigital Library
18. Lensch, H. P. A., Kautz, J., Goesele, M., Heidrich, W., and Seidel, H.-P. 2003. Image-based reconstruction of spatial appearance and geometric detail. ACM ToG 22, 2. Google ScholarDigital Library
19. Marcato Jr, R. W. 1998. Optimizing an inverse warper. PhD thesis, Massachusetts Institute of Technology.Google Scholar
20. Mitra, N. J., Guibas, L. J., and Pauly, M. 2006. Partial and approximate symmetry detection for 3d geometry. ACM ToG, 560–568. Google ScholarDigital Library
21. Mitra, N. J., Guibas, L., and Pauly, M. 2007. Symmetrization. ACM ToG 26, 3, #63, 1–8. Google ScholarDigital Library
22. Munich, M. E., and Perona, P. 1999. Continuous dynamic time warping for translation-invariant curve alignment with applications to signature verification. In ICCV, vol. 1.Google Scholar
23. Nan, L., Xie, K., and Sharf, A. 2012. A search-classify approach for cluttered indoor scene understanding. ACM ToG 31, 6 (Nov.), 137:1–137:10. Google ScholarDigital Library
24. Oliva, A., and Torralba, A. 2001. Modeling the shape of the scene: A holistic representation of the spatial envelope. IJCV 42, 3 (May), 145–175. Google ScholarDigital Library
25. Oliva, A., and Torralba, A. 2006. Building the gist of a scene: The role of global image features in recognition. Progress in Brain Research 155, 23–36.Google ScholarCross Ref
26. Osada, R., Funkhouser, T., Chazelle, B., and Dobkin, D. 2002. Shape distributions. ACM ToG 21 (October), 807–832. Google ScholarDigital Library
27. Ovsjanikov, M., Li, W., Guibas, L., and Mitra, N. J. 2011. Exploration of continuous variability in collections of 3d shapes. ACM ToG 30, 4, 33:1–33:10. Google ScholarDigital Library
28. Rusinkiewicz, S., and Levoy, M. 2001. Efficient variants of the ICP algorithm. In 3DIM, 145–152.Google Scholar
29. Saxena, A., Sun, M., and Ng, A. Y. 2009. Make3d: Learning 3d scene structure from a single still image. IEEE TPAMI 31, 5 (May), 824–840. Google ScholarDigital Library
30. Shen, C.-H., Fu, H., Chen, K., and Hu, S.-M. 2012. Structure recovery by part assembly. ACM ToG 31, 6, 180:1–180:11. Google ScholarDigital Library
31. Sorkine, O., Cohen-Or, D., Lipman, Y., Alexa, M., Rössl, C., and Seidel, H.-P. 2004. Laplacian surface editing. CGF, 175–184. Google ScholarDigital Library
32. Sumner, R. W., Schmid, J., and Pauly, M. 2007. Embedded deformation for shape manipulation. ACM ToG 26, 3 (July). Google ScholarDigital Library
33. Sun, M., Kumar, S. S., Bradski, G., and Savarese, S. 2011. Toward automatic 3d generic object modeling from one single image. In 3DIMPVT, IEEE. Google ScholarDigital Library
34. Szeliski, R., Zabih, R., Scharstein, D., Veksler, O., Kolmogorov, V., Agarwala, A., Tappen, M., and Rother, C. 2008. A comparative study of energy minimization methods for markov random fields with smoothness-based priors. IEEE TPAMI 30, 6 (June), 1068–1080. Google ScholarDigital Library
35. Wang, Y., Gong, M., Wang, T., Cohen-Or, D., Zhang, H., and Chen, B. 2013. Projective analysis for 3d shape segmentation. ACM ToG 32, 6 (Nov.), 192:1–192:12. Google ScholarDigital Library
36. Wu, T.-P., Sun, J., Tang, C.-K., and Shum, H.-Y. 2008. Interactive normal reconstruction from a single image. ACM ToG, 119:1–119:9. Google ScholarDigital Library
37. Xu, K., Zheng, H., Zhang, H., Cohen-Or, D., Liu, L., and Xiong, Y. 2011. Photo-inspired model-driven 3d object modeling. ACM ToG 30, 4 (July), 80:1–80:10. Google ScholarDigital Library
38. Zheng, Y., Chen, X., Cheng, M.-M., Zhou, K., Hu, S.-M., and Mitra, N. J. 2012. Interactive images: Cuboid proxies for smart image manipulation. ACM ToG 31, 4, 99:1–99:11. Google ScholarDigital Library
39. Zia, Z., Stark, M., Schiele, B., and Schindler, K. 2013. Detailed 3d representations for object recognition and modeling. IEEE TPAMI 35, 11, 2608–2623. Google ScholarDigital Library