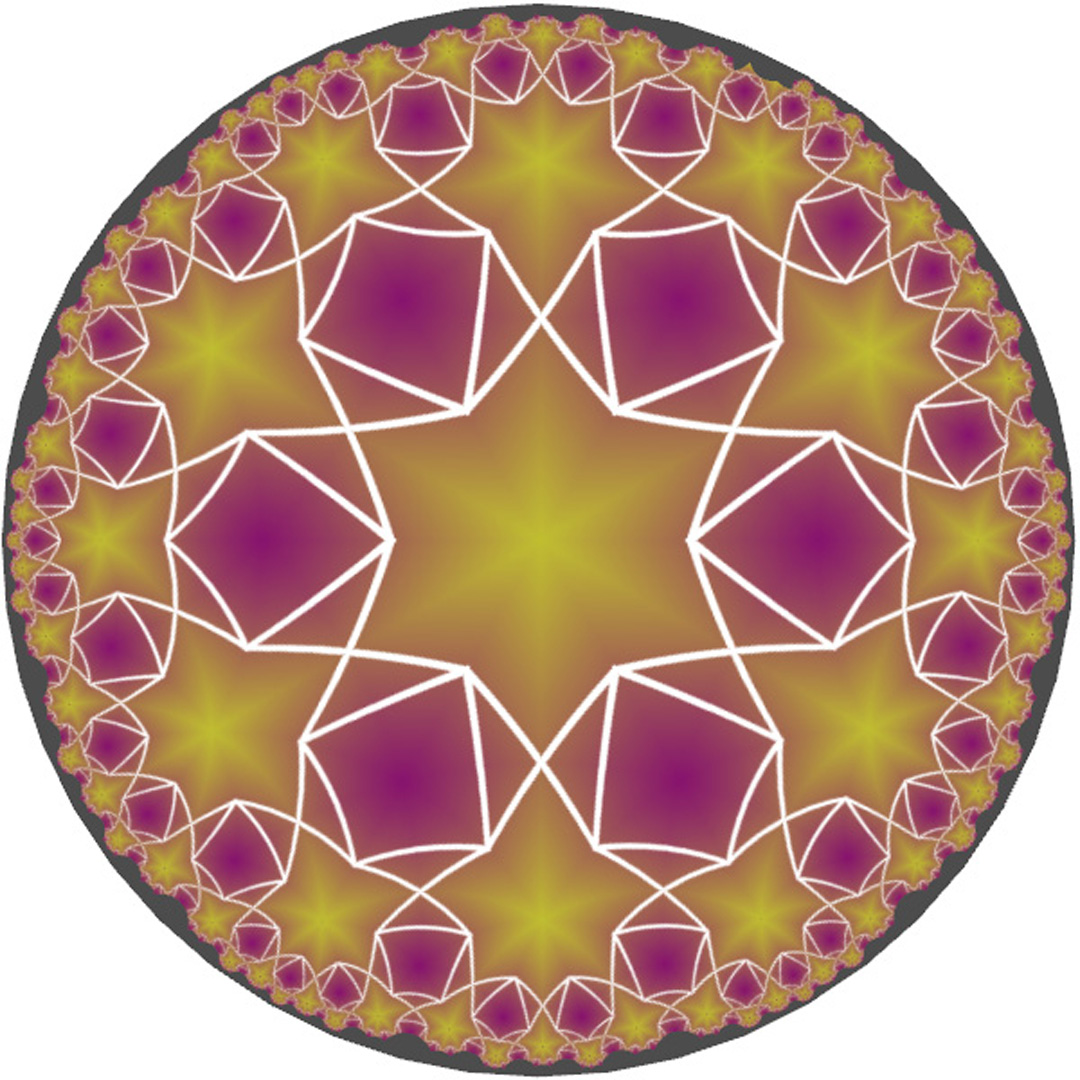
“EPINET: euclidean patterns in non-euclidean tilings” by Robins, Ramsden and Hyde
Conference:
Type(s):
Title:
- EPINET: euclidean patterns in non-euclidean tilings
Presenter(s)/Author(s):
Abstract:
We present a method for generating 3D euclidean periodic networks from 2D hyperbolic tilings. We utilize triply-periodic minimal surfaces (TPMS) as a mathematical scaffold to guide this process. These surfaces have an intrinsic hyperbolic geometry as well as an underlying set of discrete hyperbolic symmetries, allowing decoration with tilings of matching symmetry. Hyperbolic tilings of a given symmetry can be enumerated (up to finite complexity), projected onto the surface, and used to derive a labeled quotient graph of nodes and edges, representing a 3D periodic net. Although we have visualized intermediate geometries for this process, it is performed entirely as a topological computation using only neighborhood relationships and labels. The final net geometry is derived from the labeled graph, using Systre [Delgado-Friedrichs 2006], enabling uniqueness and 3D space-group identification. We have published the results of these computations at the EPINET website [Ramsden et al. 2005] for an initial sample of tilings, resulting in an online database of many thousands of 3D nets, each with their own webpage, which can be data mined via geometric and topological properties. Tiling combinatorics can provide a rich palette of both geometric and image data, only a fraction of which has been currently explored.
References:
1. Delgado-Friedrichs, O. 2006. Gavrog generation, analysis, and visualization of reticular ornaments using gavrog. http://www.gavrog.org.
2. Ramsden, S., Robins, V., Hyde, S., and Hungerford, S. 2005. Epinet: Euclidean patterns in non-euclidean tilings. http://epinet.anu.edu.au.
Additional Images: