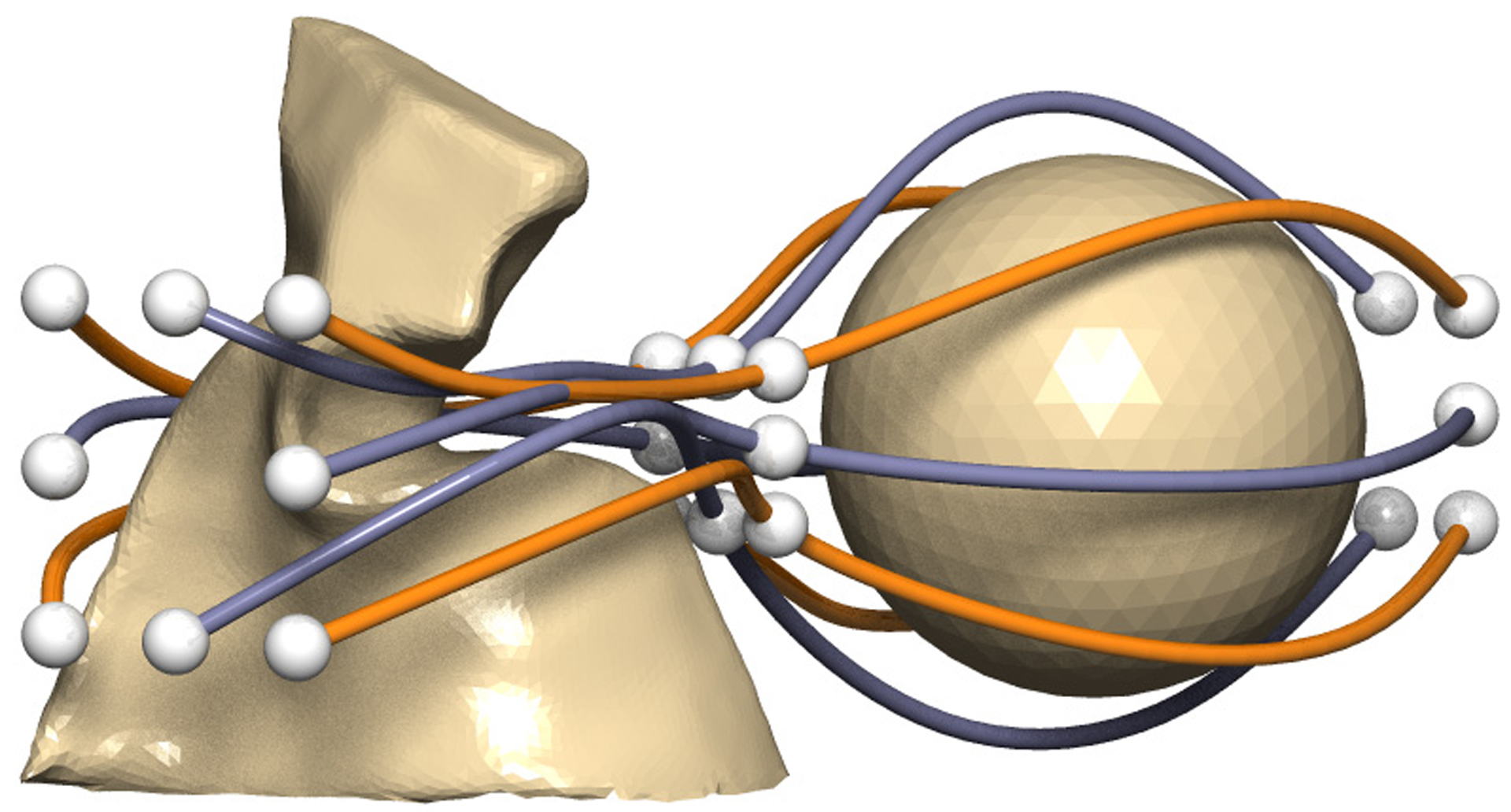
“Energy-minimizing splines in manifolds” by Hofer and Pottmann

Variational interpolation in curved geometries has many applications, so there has always been demand for geometrically meaningful and efficiently computable splines in manifolds. We extend the definition of the familiar cubic spline curves and splines in tension, and we show how to compute these on parametric surfaces, level sets, triangle meshes, and point samples of surfaces. This list is more comprehensive than it looks, because it includes variational motion design for animation, and allows the treatment of obstacles via barrier surfaces. All these instances of the general concept are handled by the same geometric optimization algorithm, which minimizes an energy of curves on surfaces of arbitrary dimension and codimension.

1. ADAMSON, A., AND ALEXA, M. 2003. Approximating and intersecting surfaces from points. In Geometry Processing 2003, Eurographics, 245–254. Google ScholarDigital Library
2. ALEXA, M., BEHR, J., COHEN, D., FLEISHMAN, S., LEVIN, D., AND SILVA, C. T. 2003. Computing and rendering point set surfaces. IEEE Trans. Visualization Comp. Graph. 9, 1, 3–15. Google ScholarDigital Library
3. ARNOL’D, V. I. 1989. Mathematical Methods of Classical Mechanics. Springer.Google Scholar
4. BARR, A. H., CURRIN, B., GABRIEL, S., AND HUGHES, J. F. 1992. Smooth interpolation of orientations with angular velocity constraints using quaternions. Computer Graphics (Proceedings of ACM SIGGRAPH 92), 26, 2, 313–320. Google ScholarDigital Library
5. BELTA, C., AND KUMAR, V. 2002. An SVD-projection method for interpolation on SE(3). IEEE Trans. Robotics Automation 18, 3, 334–345.Google ScholarCross Ref
6. BLAKE, A., AND ISARD, M. 1998. Active Contours. Springer.Google Scholar
7. BOHL, H. 1999. Kurven minimaler Energie auf getrimmten Flächen. PhD thesis, Univ. Stuttgart.Google Scholar
8. BRUNNETT, G., AND CROUCH, P. E. 1994. Elastic curves on the sphere. Adv. Comput. Math. 2, 23–40.Google ScholarCross Ref
9. BRUNNETT, G., HAGEN, H., AND SANTARELLI, P. 1993. Variational design of curves and surfaces. Surveys Math. Ind. 3, 1–27.Google Scholar
10. CAMARINHA, M., LEITE, F. S., AND CROUCH, P. E. 2001. On the geometry of Riemannian cubic polynomials. Diff. Geom. Applic. 15, 107–135.Google ScholarCross Ref
11. CASELLES, V., KIMMEL, R., AND SAPIRO, G. 1997. Geodesic active contours. Int. J. Comp. Vision 22, 61–79. Google ScholarDigital Library
12. CHENG, B. T., BURCHARD, P., MERRIMAN, B., AND OSHER, S. 2002. Motion of curves constrained on surfaces using a level set approach. Journal of Computational Physics 175, 2, 604–644. Google ScholarDigital Library
13. DO CARMO, M. P. 1976. Differential Geometry of Curves and Surfaces. Prentice-Hall.Google Scholar
14. FLETCHER, R. 1987. Practical Methods of Optimization. Wiley. Google ScholarDigital Library
15. GABRIEL, S., AND KAJIYA, J. 1985. Spline interpolation in curved space. In ACM SIGGRAPH 85 course notes for State of the Art Image Synthesis, ACM Press / ACM SIGGRAPH.Google Scholar
16. HARTMANN, E. 1999. On the curvature of curves and surfaces defined by normalforms. Comp. Aided Geom. Des. 16, 355–376. Google ScholarDigital Library
17. HOFER, M., POTTMANN, H., AND RAVANI, B. 2003. Geometric design of motions constrained by a contacting surface pair. Comp. Aided Geom. Des. 20, 8–9, 523–547. Google ScholarDigital Library
18. HORN, B. K. P. 1987. Closed form solution of absolute orientation using unit quaternions. J. Optical Soc. A 4, 629–642.Google ScholarCross Ref
19. HOSCHEK, J., AND LASSER, D. 1993. Fundamentals of Computer Aided Geometric Design. A. K. Peters. Google ScholarDigital Library
20. JÜTTLER, B., AND WAGNER, M. 2002. Kinematics and animation. In Handbook of Computer Aided Geometric Design, G. Farin, M. S. Kim, and J. Hoschek, Eds. Elsevier, 723–748.Google Scholar
21. KASS, M., WITKIN, A., AND TERZOPOULOS, D. 1987. Snakes: Active contour models. Intl. J. of Comp. Vision 1, 321–331.Google ScholarCross Ref
22. KELLEY, C. T. 1999. Iterative Methods for Optimization. SIAM.Google Scholar
23. KHANEJA, N., MILLER, M. I., AND GRENANDER, U. 1998. Dynamic programming generation of curves on brain surfaces. IEEE PAMI 20, 11, 1260–1265. Google ScholarDigital Library
24. KIMMEL, R., MALLADI, R., AND SOCHEN, N. 2000. Images as embedded maps and minimal surfaces: movies, color, texture, and volumetric medical images. Int. J. of Comp. Vision 39, 111–129. Google ScholarDigital Library
25. KOBBELT, L., AND SCHRÖDER, P. 1998. A multiresolution framework for variational subdivision. ACM Transactions on Graphics 17, 4, 209–237. Google ScholarDigital Library
26. LEE, Y., AND LEE, S. 2002. Geometric snakes for triangular meshes. Computer Graphics Forum 21, 3, 229–238.Google ScholarCross Ref
27. LEVIN, D. 2004. Mesh-independent surface interpolation. In Geometric Modeling for Scientific Visualization, G. Brunnett, B. Hamann, H. Müller, and L. Linsen, Eds. Springer, 37–50.Google Scholar
28. MALLADI, R. 2002. Geometric Methods in Bio-Medical Image Processing. Springer.Google Scholar
29. MEEK, D. S., ONG, B. H., AND WALTON, D. J. 2003. Constrained interpolation with rational cubics. Comp. Aided Geom. Design 20, 5, 253–275. Google ScholarDigital Library
30. MEMOLI, F., AND SAPIRO, G. 2001. Fast computation of weighted distance functions and geodesics on implicit hyper-surfaces. J. Comput. Phys. 173, 2, 730–764. Google ScholarDigital Library
31. MORETON, H., AND SEQUIN, C. 1993. Scale invariant minimum cost curves: fair and robust design implements. Computer Graphics Forum 12, 473–484.Google ScholarCross Ref
32. NEUBERGER, J. W. 1997. Sobolev Gradients and Differential Equations. Springer.Google Scholar
33. NOAKES, L., HEINZINGER, G., AND PADEN, B. 1989. Cubic splines on curved spaces. IMA J. Math. Cont. & Inf. 6, 465–473.Google ScholarCross Ref
34. NOAKES, L. 2003. Null cubics and Lie quadratics. J. Math. Physics 44, 3, 1436–1448.Google ScholarCross Ref
35. OPFER, G., AND OBERLE, H. J. 1988. The derivation of cubic splines with obstacles by methods of optimization and optimal control. Numer. Math. 52, 17–31. Google ScholarDigital Library
36. OSHER, S., AND FEDKIW, R. 2002. The Level Set Method and Dynamic Implicit Surfaces. Springer.Google Scholar
37. PARK, F., AND RAVANI, B. 1997. Smooth invariant interpolation of rotations. ACM Transactions on Graphics 16, 3, 277–295. Google ScholarDigital Library
38. PAULY, M., KEISER, R., KOBBELT, L., AND GROSS, M. 2003. Shape modeling with point-sampled geometry. ACM Transactions on Graphics 22, 3, 641–650. Google ScholarDigital Library
39. POTTMANN, H., AND HOFER, M. 2003. A variational approach to spline curves on surfaces. Tech. Rep. 115, TU Wien, Inst. Geometry, http://www.geometrie.tuwien.ac.at/ig/papers/vscs.pdf.Google Scholar
40. POTTMANN, H., AND HOFER, M. 2004. Algorithms for constrained minimization of quadratic functions — geometry and convergence analysis. Tech. Rep. 121, TU Wien, Geometry Preprint. http://www.geometrie.tuwien.ac.at/ig/papers/foot.pdf.Google Scholar
41. POTTMANN, H., STEINER, T., HOFER, M., HAIDER, C., AND HANBURY, A. 2004. The isophotic metric and its application to feature sensitive morphology on surfaces. In Proceedings of ECCV 2004. Springer.Google ScholarCross Ref
42. RAMAMOORTHI, R., AND BARR, A. 1997. Fast construction of accurate quaternion splines. In Proceedings of ACM SIGGRAPH 1997, ACM Press / ACM SIGGRAPH, New York, ACM, 287–292. Google ScholarDigital Library
43. SAPIRO, G. 2001. Geometric Partial Differential Equations and Image Analysis. Cambridge Univ. Press. Google ScholarDigital Library
44. SCHWEIKERT, D. 1966. An interpolating curve using a spline in tension. J. Math. Phys. 45, 312–317.Google ScholarCross Ref
45. SPIVAK, M. 1975. A Comprehensive Introduction to Differential Geometry. Publish or Perish.Google Scholar
46. TSAI, R. 2002. Rapid and accurate computation of the distance function using grids. J. Comput. Phys. 178, 1, 175–195. Google ScholarDigital Library
47. ZHAO, H.-K. 2004. A fast sweeping method for Eikonal equations. Mathematics of Computation. to appear.Google Scholar