“Eliminating topological errors in neural network rotation estimation using self-selecting ensembles” by Xiang

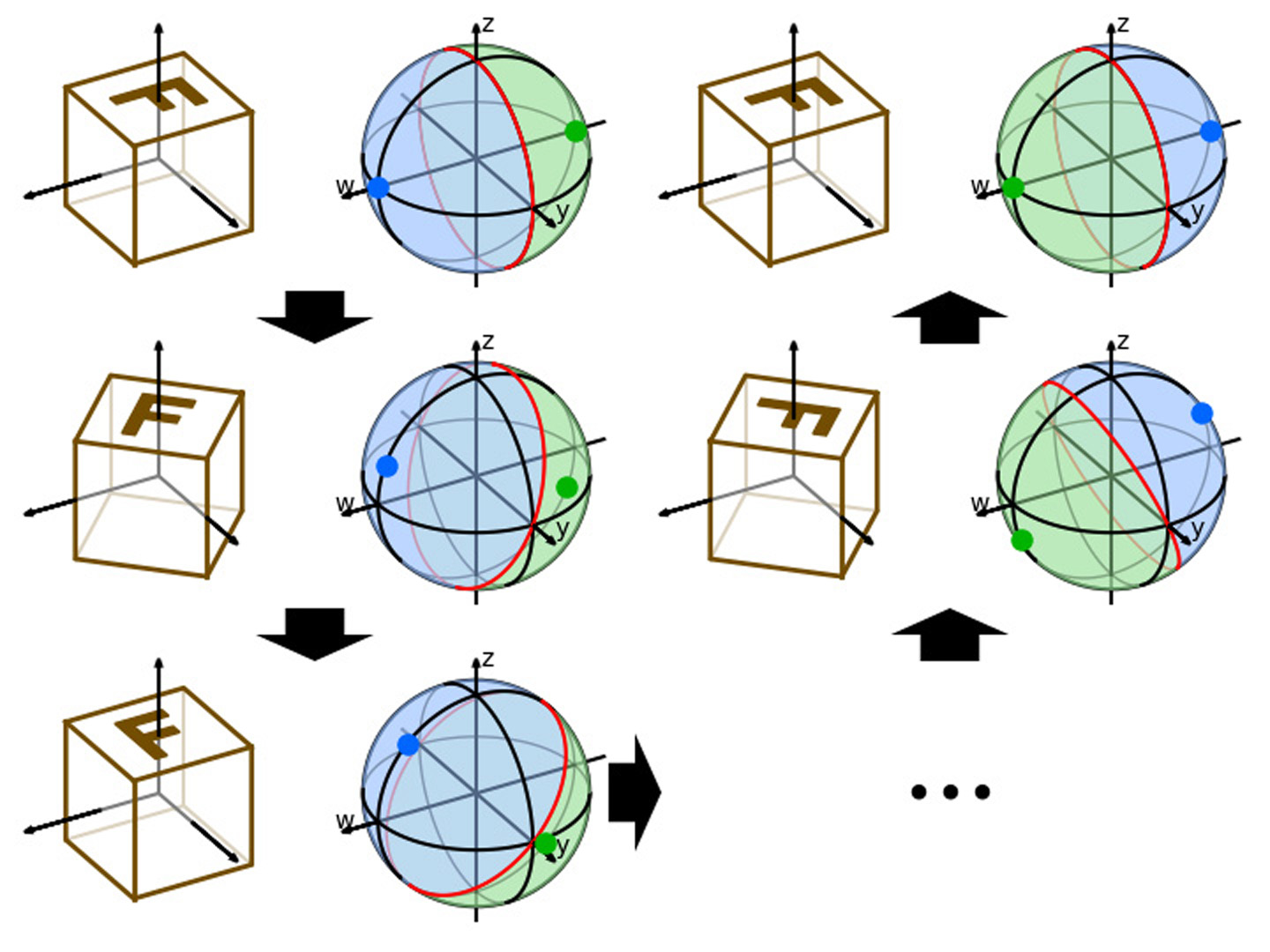
Many problems in computer graphics and computer vision applications involves inferring a rotation from a variety of different forms of inputs. With the increasing use of deep learning, neural networks have been employed to solve such problems. However, the traditional representations for 3D rotations, the quaternions and Euler angles, are found to be problematic for neural networks in practice, producing seemingly unavoidable large estimation errors. Previous researches has identified the discontinuity of the mapping from SO(3) to the quaternions or Euler angles as the source of such errors, and to solve it, embeddings of SO(3) have been proposed as the output representation of rotation estimation networks instead. In this paper, we argue that the argument against quaternions and Euler angles from local discontinuities of the mappings from SO(3) is flawed, and instead provide a different argument from the global topological properties of SO(3) that also establishes the lower bound of maximum error when using quaternions and Euler angles for rotation estimation networks. Extending from this view, we discover that rotation symmetries in the input object causes additional topological problems that even using embeddings of SO(3) as the output representation would not correctly handle. We propose the self-selecting ensemble, a topologically motivated approach, where the network makes multiple predictions and assigns weights to them. We show theoretically and with experiments that our methods can be combined with a wide range of different rotation representations and can handle all kinds of finite symmetries in 3D rotation estimation problems.

1. Paolo Cignoni, Marco Callieri, Massimiliano Corsini, Matteo Dellepiane, Fabio Ganovelli, and Guido Ranzuglia. 2008. MeshLab: an Open-Source Mesh Processing Tool. In Eurographics Italian Chapter Conference, Vittorio Scarano, Rosario De Chiara, and Ugo Erra (Eds.). The Eurographics Association. Google ScholarCross Ref
2. Massimiliano Corsini, Paolo Cignoni, and Roberto Scopigno. 2012. Efficient and Flexible Sampling with Blue Noise Properties of Triangular Meshes. IEEE Transaction on Visualization and Computer Graphics 18, 6 (2012), 914–924. http://vcg.isti.cnr.it/Publications/2012/CCS12 Google ScholarDigital Library
3. Erik W Grafarend and Wolfgang Kühnel. 2011. A minimal atlas for the rotation group SO (3). GEM-International Journal on Geomathematics 2, 1 (2011), 113–122.Google ScholarCross Ref
4. Allen Hatcher. 2002. Algebraic Topology. Cambridge University Press. Electronic version available at https://pi.math.cornell.edu/~hatcher/AT/ATpage.html.Google Scholar
5. Jake Levinson, Carlos Esteves, Kefan Chen, Noah Snavely, Angjoo Kanazawa, Afshin Rostamizadeh, and Ameesh Makadia. 2020. An analysis of svd for deep rotation estimation. arXiv preprint arXiv:2006.14616 (2020).Google Scholar
6. Siddharth Mahendran, Haider Ali, and René Vidal. 2017. 3d pose regression using convolutional neural networks. In Proceedings of the IEEE International Conference on Computer Vision Workshops. 2174–2182.Google Scholar
7. Siddharth Mahendran, Haider Ali, and Rene Vidal. 2018. A mixed classification-regression framework for 3d pose estimation from 2d images. arXiv preprint arXiv:1805.03225 (2018).Google Scholar
8. G Dias Pais, Srikumar Ramalingam, Venu Madhav Govindu, Jacinto C Nascimento, Rama Chellappa, and Pedro Miraldo. 2020. 3dregnet: A deep neural network for 3d point registration. In Proceedings of the IEEE/CVF conference on computer vision and pattern recognition. 7193–7203.Google ScholarCross Ref
9. Valentin Peretroukhin, Matthew Giamou, David M Rosen, W Nicholas Greene, Nicholas Roy, and Jonathan Kelly. 2020. A smooth representation of belief over so (3) for deep rotation learning with uncertainty. arXiv preprint arXiv:2006.01031 (2020).Google Scholar
10. Omid Poursaeed, Guandao Yang, Aditya Prakash, Qiuren Fang, Hanqing Jiang, Bharath Hariharan, and Serge Belongie. 2018. Deep fundamental matrix estimation without correspondences. In Proceedings of the European Conference on Computer Vision (ECCV) Workshops. 0–0.Google Scholar
11. Charles R. Qi, Hao Su, Kaichun Mo, and Leonidas J. Guibas. 2017. Pointnet: Deep learning on point sets for 3d classification and segmentation. In Proceedings of the IEEE conference on computer vision and pattern recognition. 652–660.Google Scholar
12. Ashutosh Saxena, Justin Driemeyer, and Andrew Y. Ng. 2009. Learning 3-d object orientation from images. In 2009 IEEE International Conference on Robotics and Automation. IEEE, 794–800.Google Scholar
13. Hao Su, Charles R Qi, Yangyan Li, and Leonidas J Guibas. 2015. Render for cnn: Viewpoint estimation in images using cnns trained with rendered 3d model views. In Proceedings of the IEEE International Conference on Computer Vision. 2686–2694.Google ScholarDigital Library
14. Floris Takens. 1968. The minimal number of critical points of a function on a compact manifold and the Lusternik-Schnirelman category. Inventiones mathematicae 6, 3 (1968), 197–244.Google Scholar
15. Shubham Tulsiani and Jitendra Malik. 2015. Viewpoints and keypoints. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 1510–1519.Google ScholarCross Ref
16. Yu Xiang, Tanner Schmidt, Venkatraman Narayanan, and Dieter Fox. 2018. Posecnn: A convolutional neural network for 6d object pose estimation in cluttered scenes. In Robotics: Science and Systems (RSS).Google Scholar
17. Xingyi Zhou, Xiao Sun, Wei Zhang, Shuang Liang, and Yichen Wei. 2016. Deep kinematic pose regression. In European Conference on Computer Vision. Springer, 186–201.Google ScholarCross Ref
18. Yi Zhou, Connelly Barnes, Jingwan Lu, Jimei Yang, and Hao Li. 2019. On the continuity of rotation representations in neural networks. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition. 5745–5753.Google ScholarCross Ref