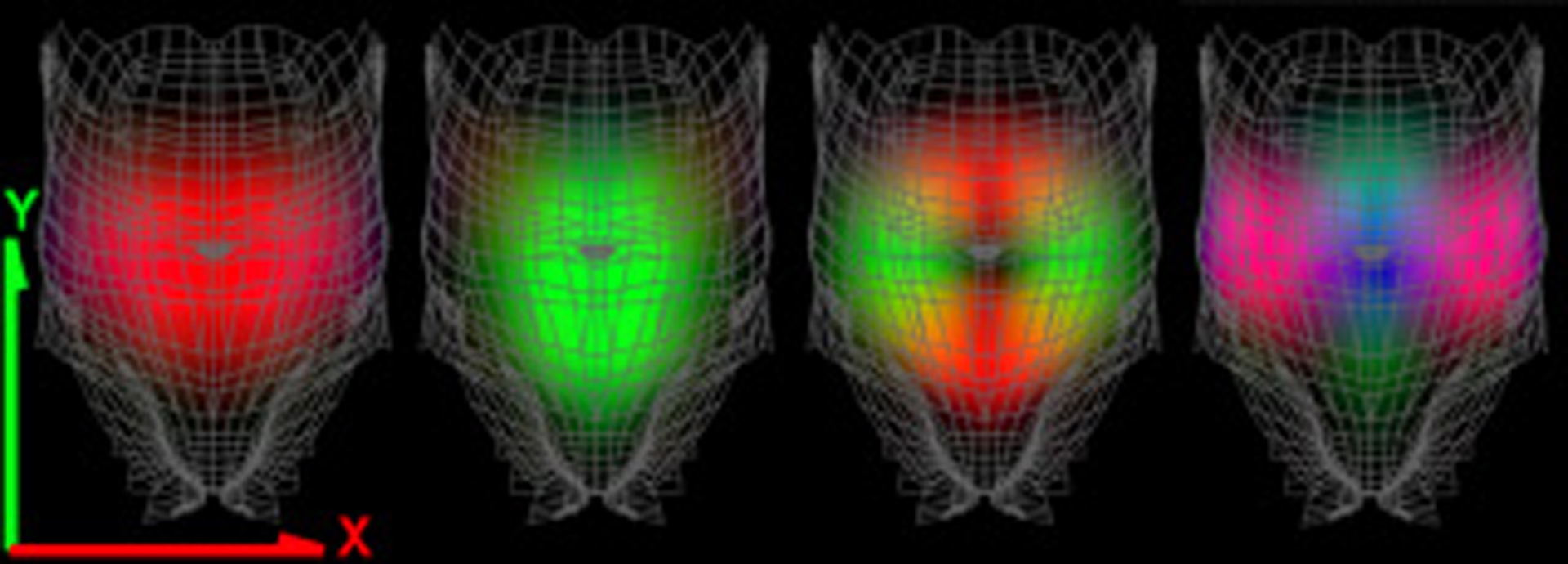
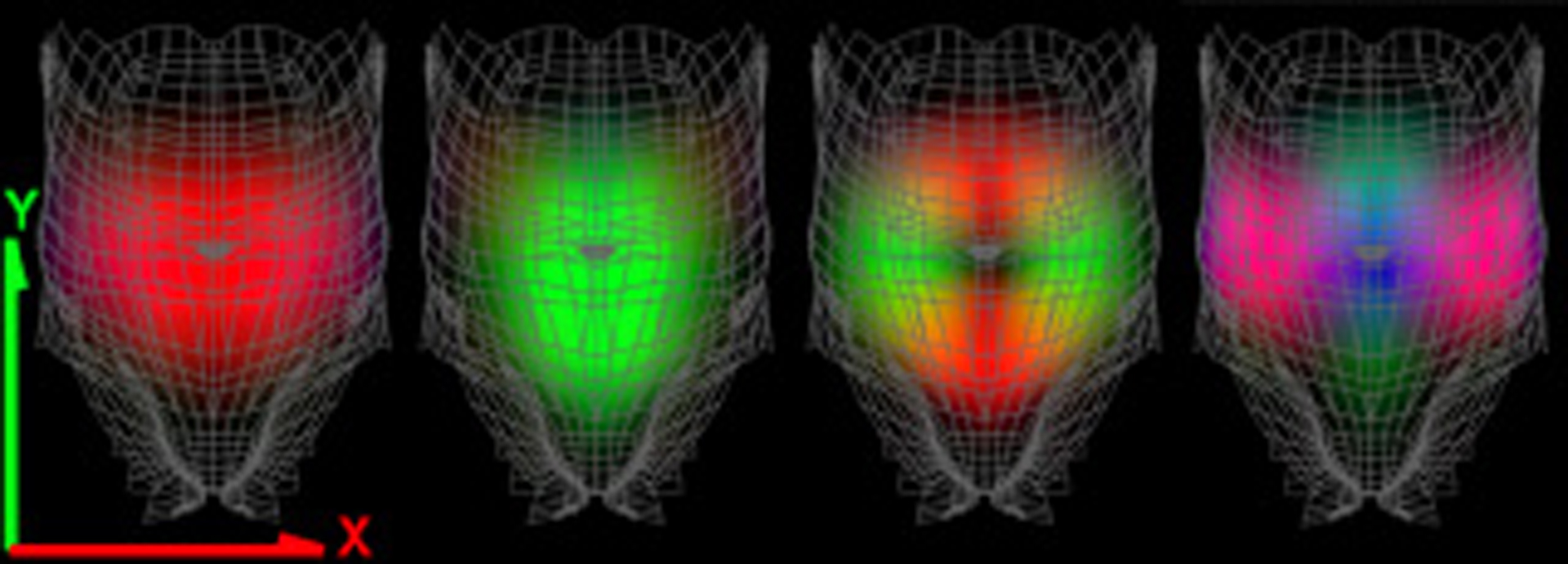
“DyRT: dynamic response textures for real time deformation simulation with graphics hardware”

In this paper we describe how to simulate geometrically complex, interactive, physically-based, volumetric, dynamic deformation models with negligible main CPU costs. This is achieved using a Dynamic Response Texture, or DyRT, that can be mapped onto any conventional animation as an optional rendering stage using commodity graphics hardware. The DyRT simulation process employs precomputed modal vibration models excited by rigid body motions. We present several examples, with an emphasis on bone-based character animation for interactive applications.

1. D. Baraff and A. Witkin. Dynamic Simulation of Non-penetrating Flexible Bodies. In Computer Graphics (SIGGRAPH 92 Conference Proceedings), pages 303-308, 1992. Google Scholar
2. D. Baraff and A. Witkin. Large Steps in Cloth Simulation. In SIGGRAPH 98 Conference Proceedings, pages 43-54, 1998. Google Scholar
3. A. Barr. Global and Local Deformations of Solid Primitives. In Computer Graphics (SIGGRAPH 84 Conference Proceedings), volume 18, pages 21-30, 1984. Google Scholar
4. C. Basdogan. Real-time Simulation of Dynamically Deformable Finite Element Models Using Modal Analysis and Spectral Lanczos Decomposition Methods. In Medicine Meets Virtual Reality (MMVR’2001), pages 46-52, 2001.Google Scholar
5. J. E. Chadwick, D. R. Haumann, and R. E. Parent. Layered Construction of Deformable Animated Characters. In Computer Graphics (SIGGRAPH 89 Conference Proceedings), volume 23, pages 243-252, 1989. Google Scholar
6. G. Debunne, M. Desbrun, A. Barr, and M.-P. Cani. Dynamic real-time deformations using space and time adaptive sampling. In SIGGRAPH O1 Conference Proceedings, pages 31-36, 2001. Google Scholar
7. G. Dhondt and K. Wittig. CalculiX: A Free Software Three-Dimensional Structural Finite Element Program.Google Scholar
8. M. Friedmann and A. Pentland. Distributed physical simulation. In Third Eurographics Workshop on Animation and Simulation, pages 1-17, 1992.Google Scholar
9. J. Gourret, N. Magnenat-Thalmann, and D. Thalmann. Simulation of Object and Human Skin Deformations in a Grasping Task. In Computer Graphics (SIGGRAPH 89 Conference Proceedings), volume 23, pages 21-29, 1989. Google Scholar
10. D. L. James. Multiresolution Green’s Function Methods for Interactive Simulation of Large-scale Elastostatic Objects and Other Physical Systems in Equilibrium. PhD thesis, Institute of Applied Mathematics, University of British Columbia, Vancouver, British Columbia, Canada, 2001. Google Scholar
11. D. L. James and D. K. Pai. ARTDEFO: Accurate Real Time Deformable Objects. In SIGGRAPH 99 Conference Proceedings, pages 65-72, 1999. Google Scholar
12. Y. Lee, D. Terzopoulos, and K. Walters. Realistic Modeling for Facial Animation. In SIGGRAPH 95 Conference Proceedings, pages 55-62, 1995. Google Scholar
13. R. Lehoucq, D. Sorensen, and C. Yang. ARPACK Users’ Guide: Solution of large scale eigenvalue problems with implicitly restarted Arnoldi methods. Technical report, Comp. and Applied Mathematics, Rice Univ., 1997.Google Scholar
14. E. Lindholm, M. J. Kilgard, and H. Moreton. A User-Programmable Vertex Engine. In SIGGRAPH 2001 Conference Proceedings, pages 149-158, 2001. Google Scholar
15. D. Metaxas and D. Terzopoulos. Dynamic Deformation of Solid Primitives with Constraints. In Computer Graphics (SIGGRAPH 98 Conference Proceedings), volume 26, pages 309-312, 1992. Google Scholar
16. R. M. Murray, Z. Li, and S. S. Sastry. A Mathematical Introduction to Robotic Manipulation. CRC Press, Inc., 1994. Google Scholar
17. J. O’Brien, P. Cook, and G. Essl. Synthesizing Sounds from Physically Based Motion. In SIGGRAPH 01 Conference Proceedings, pages 529-536, 2001. Google Scholar
18. J. F. O’Brien and J. K. Hodgins. Graphical modeling and animation of brittle fracture. In SIGGRAPH 99 Conference Proceedings, pages 111-120, 1999. Google Scholar
19. A. Pentland and J. Williams. Good Vibrations: Modal Dynamics for Graphics and Animation. In Computer Graphics (SIGGRAPH 89 Conference Proceedings), volume 23, pages 215-222, 1989. Google Scholar
20. G. Picinbono, H. Delingette, and N. Ayache. Non-linear and anisotropic elastic soft tissue models for medical simulation. In ICRA2OO1: IEEE International Conference on Robotics and Automation, Seoul Korea, May 2001.Google Scholar
21. J. Schoberl. NETGEN – An advancing front 2D/3D-mesh generator based on abstract rules. Comput. Visual. Sci, 1:41-52, 1997.Google Scholar
22. A. A. Shebana. Theory of Vibration, Volume II: Discrete and Continuous Systems. Springer-Verlag, New York, NY, first edition, 1990.Google Scholar
23. J. Stam. Stochastic Dynamics: Simulating the Effects of Turbulence on Flexible Structures. Computer Graphics Forum, 10(3), 1997.Google Scholar
24. K. Steiglitz. A Digital Signal Processing Primer with Applications to Digital Audio and Computer Music. Addison-Wesley, New York, 1996. Google Scholar
25. D. Terzopoulos and K. Fleischer. Deformable models. The Visual Computer, 4:306-331, 1988.Google Scholar
26. K. van den Doel, P. G. Kry, and D. K. Pai. Foley Automatic: Physically-based Sound Effects for Interactive Simulations and Animations. In SIGGRAPH 01 Conference Proceedings, 2001. Google Scholar
27. J. Wilhelms and A. V. Gelder. Anatomically Based Modeling. In SIGGRAPH 97 Conference Proceedings, pages 173-180, 1997. Google Scholar
28. A. Witkin and W. Welch. Fast Animation and Control of Nonrigid Structures. In Computer Graphics (SIGGRAPH 90 Conference Proceedings), pages 243-252, 1990. Google Scholar
29. O. C. Zienkiewicz. The Finite Element Method. McGraw-Hill Book Company (UK) Limited, Maidenhead, Berkshire, England, 1977.Google Scholar