“Displaced subdivision surfaces” by Moreton, Hoppe and Lee

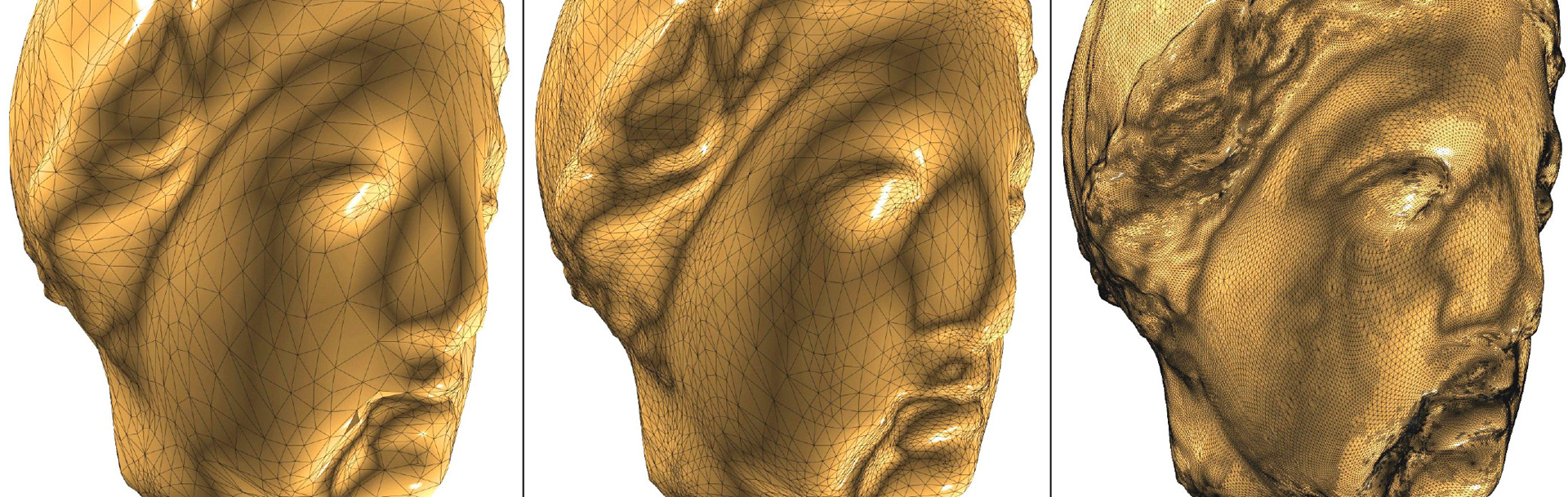
In this paper we introduce a new surface representing, the displaced subdivision surface. It represents a detailed surface model as a scalar-valued displacement over a smooth domain surface. Our representation defines both the domain surface and the displacement function using a unified subdivision framework, allowing for simple and efficient evaluation of analytic surface properties. We present a simple, automatic scheme for converting detailed geometric models into such a representation. The challenge in this conversion process is to find a simple subdivision surface that still faithfully expresses the detailed model as its offset. We demonstrate that displaced subdivision surfaces offer a number of benefits, including geometry compression, editing, animation, scalability, and adaptive rendering. In particular, the encoding of fine detail as a scalar function makes the representation extremely compact.

1. Apodaca, A. and Gritz, L. Advanced RenderMan – Creating CGI for Motion Pictures, Morgan Kaufmann, San Francisco, CA, 1999.
2. Becker, B. and Max, N. Smooth transitions between bump rendering algorithms. Proceedings of SIGGRAPH 93, Computer Graphics, Annual Conference Series, pp. 183-190.
3. Blinn, J. F. Simulation of wrinkled surfaces. Proceedings of SIGGRAPH 78, Computer Graphics, pp. 286-292.
4. Cabral, B., Max, N. and Springmeyer, R. Bidirectional reflection functions from surface bump maps. Proceedings of SIGGRAPH 87, Computer Graphics, Annual Conference Series, pp.273-281.
5. Catmull, E., and Clark, J. Recursively generated B-spline surfaces on arbitrary topological meshes. Computer Aided Design 10, pp. 350-355 (1978).
6. Certain,A.,Popovic,J.,DeRose,T.,Duchamp,T.,Salesin,D.and Stuetzle, W. Interactive multiresolution surface viewing. Proceedings of SIGGRAPH 96, Computer Graphics, Annual Conference Series, pp. 91-98.
7. Chan, K., Mann, S., and Bartels, R. World space surface pasting. Graphics Interface ’97, pp. 146-154.
8. Cohen, J., Olano, M. and Manocha, D. Appearance preserving Simplification. Proceedings of SIGGRAPH 98, Computer Graphics, Annual Conference Series, pp. 115-122.
9. Cook, R. Shade trees. Computer Graphics (Proceedings of SIGGRAPH 84), 18(3), pp. 223-231.
10. Deering, M. Geometry compression. Proceedings of SIGGRAPH 95, Computer Graphics, Annual Conference Series, pp. 13-20.
11. DeRose, T., Kass, M., and Truong, T. Subdivision surfaces in character animation. Proceedings of SIGGRAPH 98, Computer Graphics, Annual Conference Series, pp. 85-94.
12. Do Carmo, M. P. Differential Geometry of Curves and Surfaces. Prentice-Hall, Inc., Englewood Cliffs, New Jersey, 1976.
13. Doo, D., and Sabin, M. Behavior of recursive division surfaces near extraordinary points. Computer Aided Design 10, pp. 356-360 (1978).
14. Eck, M., DeRose, T., Duchamp, T., Hoppe, H., Lounsbery, M., and Stuetzle, W. Multiresolution analysis of arbitrary meshes. Proceedings of SIGGRAPH 95, Computer Graphics, Annual Conference Series, pp. 173-182.
15. Forsey, D., and Bartels, R. Surface fitting with hierarchical splines. ACM Transactions on Graphics, 14(2), pp. 134-161 (April 1995).
16. Garland, M., and Heckbert, P. Surface simplification using quadric error metrics. Proceedings of SIGGRAPH 97, Computer Graphics, Annual Conference Series, pp. 209-216.
17. Gottschalk, S., Lin, M., and Manocha, D. OBB-tree: a hierarchical structure for rapid interference detection. Proceedings of SIGGRAPH 96, Computer Graphics, Annual Conference Series, pp. 171-180.
18. Gumhold, S., and Stra~er, W. Real time compression of triangle mesh connectivity. Proceedings of SIGGRAPH 98, Computer Graphics, Annual Conference Series, pp. 133-140.
19. Gumhold, S., and H~ttner, T. Multiresolution rendering with displacement mapping. SIGGRAPH workshop on Graphics hardware, Aug 8-9, 1999.
20. Guskov, I., Vidimce, K., Sweldens, W., and Schr~der, P. Normal meshes. Proceedings of SIGGRAPH 2000, Computer Graphics, Annual Conference Series.
21. Hoppe, H., DeRose, T., Duchamp, T., Halstead, M., Jin, H., McDonald, J., Schweitzer, J., and Stuetzle, W. Piecewise smooth surface reconstruction. Proceedings of SIGGRAPH 94, Computer Graphics, Annual Conference Series, pp. 295-302.
22. Hoppe, H. Progressive meshes. Proceedings of SIGGRAPH 96, Computer Graphics, Annual Conference Series, pp. 99-108.
23. Kobbelt, L., Bareuther, T., and Seidel, H. P. Multi-resolution shape deformations for meshes with dynamic vertex connectivity. Proceedings of EUROGRAPHICS 2000, to appear.
24. Kolarov, K. and Lynch, W. Compression of functions defined on surfaces of 3D objects. In J. Storer and M. Cohn, editors, Proc. of Data Compression Conference, IEEE, pp. 281-291, 1997.
25. Krishnamurthy, V., and Levoy, M. Fitting smooth surfaces to dense polygon meshes. Proceedings of SIGGRAPH 96, Computer Graphics, Annual Conference Series, pp. 313-324.
26. Lee, A., Sweldens, W., Schr~der, P., Cowsar, L., and Dobkin, D. MAPS: Multiresolution adaptive parameterization of surfaces. Proceedings of SIGGRAPH 98, Computer Graphics, Annual Conference Series, pp. 95-104.
27. Loop, C. Smooth subdivision surfaces based on triangles. Master’s thesis, University of Utah, Department of Mathematics, 1987.
28. Lounsbery, M., DeRose, T., and Warren, J. Multiresolution analysis for surfaces of arbitrary topological type. ACM Transactions on Graphics, 16(1), pp. 34-73 (January 1997).
29. Mann, S. and Yeung, T. Cylindrical surface pasting. Technical Report, Computer Science Dept., University of Waterloo (June 1999).
30. Marschner, S., Guenter, B., and Raghupathy, S. Modeling and rendering for realistic facial animation. Submitted for publication.
31. Peercy, M., Airey, J. and Cabral, B. Efficient bump mapping hardware. Proceedings of SIGGRAPH 97, Computer Graphics, Annual Conference Series, pp. 303-306.
32. Peters, J. Local smooth surface interpolation: a classification. Computer Aided Geometric Design, 7(1990), pp. 191-195.
33. Schr~der, P., and Sweldens, W. Spherical wavelets: efficiently representing functions on the sphere. Proceedings of SIGGRAPH 95, Computer Graphics, Annual Conference Series, pp. 161-172.
34. Shoham, Y. and Gersho, A. Efficient bit allocation for an arbitrary set of quantizers. IEEE Transactions on Acoustics, Speech, and Signal Processing, Vol. 36, No. 9, pp. 1445-1453, Sept 1988.
35. Taubin, G. A signal processing approach to fair surface design. Proceedings of SIGGRAPH 95, Computer Graphics, Annual Conference Series, pp. 351-358.
36. Taubin, G. and Rossignac, J. Geometric compression through topological surgery. ACM Transactions on Graphics, 17(2), pp. 84- 115 (April 1998).
37. Taubman, D. and Zakhor, A. Multirate 3-D subband coding of video. IEEE Transactions on Image Processing, Vol. 3, No. 5, Sept, 1994.
38. Zhang, H., and Hoff, K. Fast backface culling using normal masks. Symposium on Interactive 3D Graphics, pp. 103-106, 1997.
39. Zorin, D., Schr~der, P., and Sweldens, W. Interactive multiresolution mesh editing. Proceedings of SIGGRAPH 97, Computer Graphics, Annual Conference Series, pp. 259-268.