“Depth Boost: Extended Depth Reconstruction Capability on Volumetric Display”
Conference:
Type(s):
Entry Number: 35
Title:
- Depth Boost: Extended Depth Reconstruction Capability on Volumetric Display
Presenter(s)/Author(s):
Abstract:
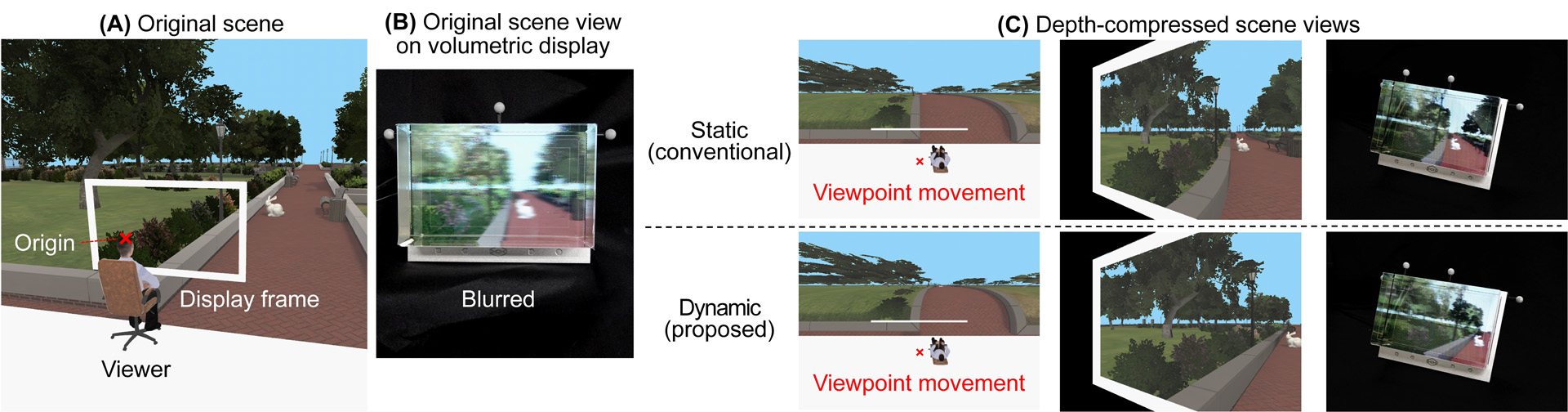
A key challenge of volumetric displays is presenting a 3D scene as if naturally existed in the physical space. However, the displayable scenes are limited because current volumetric displays do not have a substantial depth reconstruction capability to show scenes with significant depth. In this talk, we propose a dynamic depth compression method that modifies the 3D geometries of presented scenes while considering changes to the spectator’s view point such that entire scenes are fitted within a smaller depth range while maintaining the perceptual quality. Extensive depth compression induces a feeling of unnaturalness in viewers, but the results of an evaluation experiment using a volumetric display simulator indicated that a depth of just 10 cm was needed to show scenes that originally had about 50 m without an unacceptable feeling of unnaturalness. We applied our method to a real volumetric display and validated our findings through an additional user study. The results suggest that our method works well as a virtual extender of a volumetric display’s depth reconstruction capability, enabling hundreds of times larger depth reconstruction than that of current volumetric displays.
References:
H. Hoshino, F. Okano, H. Isono, and I. Yuyama. 1998. Analysis of resolution limitation of integral photography. J. Opt. Soc. Am. A 15, 8 (Aug 1998), 2059–2065. A. Isaksen, L. McMillan, and S. J. Gortler. 2000. Dynamically Reparameterized Light Fields (SIGGRAPH ’00). 297–306.
M. Lang, A. Hornung, O. Wang, S. Poulakos, A. Smolic, and M. Gross. 2010. Nonlinear Disparity Mapping for Stereoscopic 3D. ACM Trans. Graph. 29, 4, Article 75 (July 2010), 75:1–75:10 pages.
Y. Sawahata and T. Morita. 2018. Estimating Depth Range Required for 3-D Displays to Show Depth-Compressed Scenes Without Inducing Sense of Unnaturalness. IEEE Trans. Broadcast. 64, 2 (June 2018), 488–497.