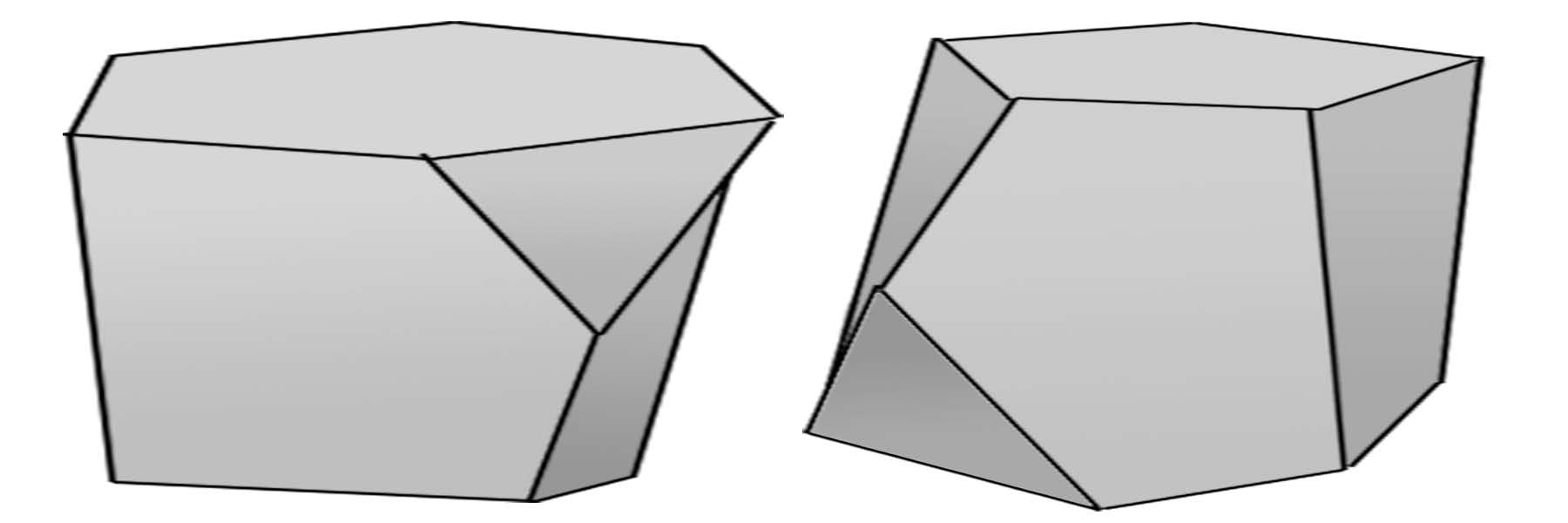
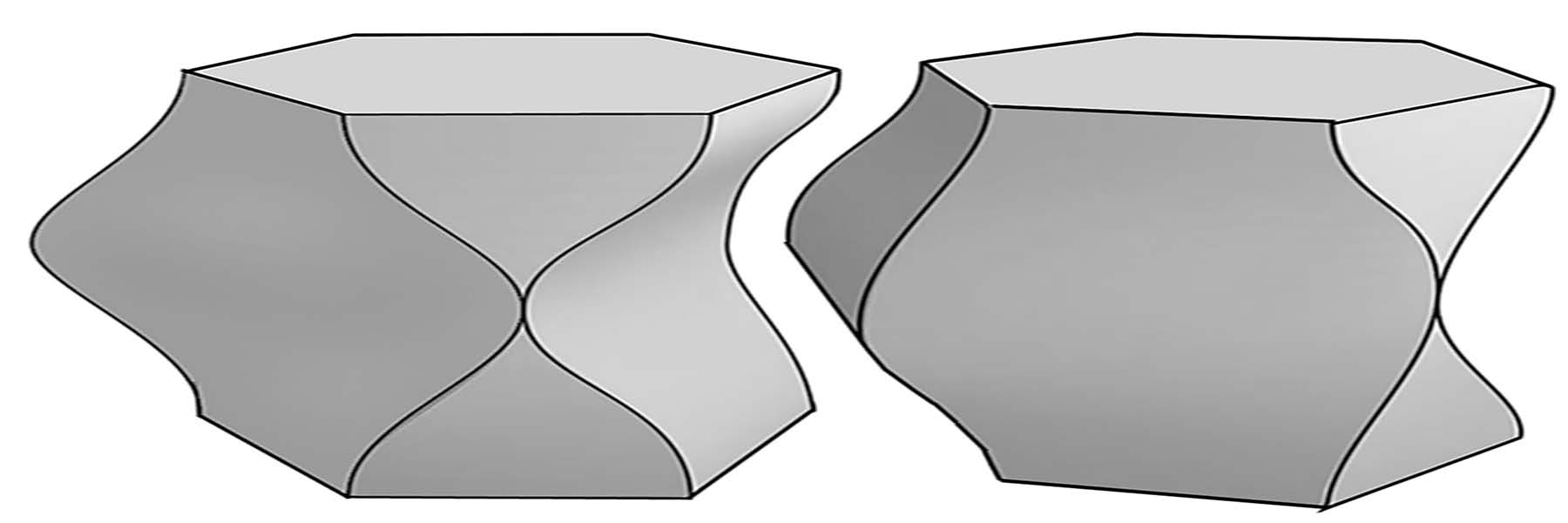
“Delaunay Lofts: A New Class of Space-Filling Shapes” by Subramanian, Krishnamurthy, Eng and Akleman
Conference:
Type(s):
Entry Number: 81
Title:
- Delaunay Lofts: A New Class of Space-Filling Shapes
Presenter(s)/Author(s):
Abstract:
We have developed an approach to construct and design a new class of space-filling shapes, which we call Delaunay Lofts. Our approach is based on interpolation of a stack of planar tiles whose dual tilings are Delaunay diagrams. We construct control curves that interpolate Delaunay vertices. Voronoi decomposition of the volume using these control curves as Voronoi sites gives us lofted interpolation of original polygons in planar tiles. This, combined with the use of wallpaper symmetries allows for the design of space filling shapes in 3-space. In the poster exhibition, we will also demonstrate 3D printed examples of the new class of shapes (See Figures 1 and 3).
References:
- Pedro Gómez-Gálvez, Pablo Vicente-Munuera, Antonio Tagua, Cristina Forja, Ana M Castro, Marta Letrán, Andrea Valencia-Expósito, Clara Grima, Marina Bermúdez-Gallardo, Óscar Serrano-Pérez-Higueras, and others. 2018. Scutoids are a geometrical solution to three-dimensional packing of epithelia. Nature communications 9, 1
(2018), 2960. - Vinod Srinivasan, Ergun Akleman, and Jianer Chen. 2002. Interactive construction of multi-segment curved handles. In Proceedings of 10th Pacific Conference on Computer Graphics and Applications, 2002. IEEE, New Jersey, 429–430.
Keyword(s):
Additional Images: