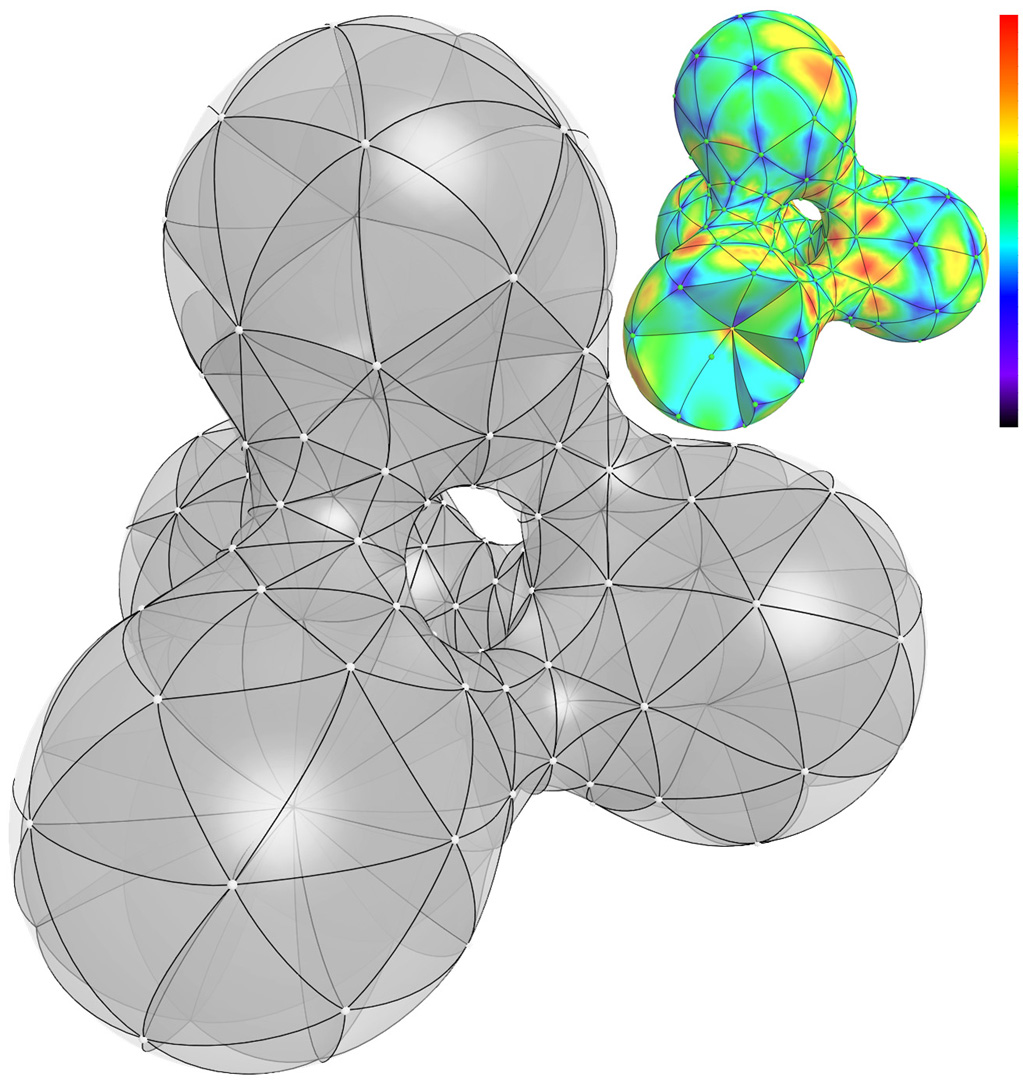
“Curved optimal delaunay triangulation” by Feng, Alliez, Busé, Delingette and Desbrun
Conference:
Type(s):
Entry Number: 61
Title:
- Curved optimal delaunay triangulation
Session/Category Title: Cleaning Up the Mesh We Made
Presenter(s)/Author(s):
Moderator(s):
Abstract:
Meshes with curvilinear elements hold the appealing promise of enhanced geometric flexibility and higher-order numerical accuracy compared to their commonly-used straight-edge counterparts. However, the generation of curved meshes remains a computationally expensive endeavor with current meshing approaches: high-order parametric elements are notoriously difficult to conform to a given boundary geometry, and enforcing a smooth and non-degenerate Jacobian everywhere brings additional numerical difficulties to the meshing of complex domains. In this paper, we propose an extension of Optimal Delaunay Triangulations (ODT) to curved and graded isotropic meshes. By exploiting a continuum mechanics interpretation of ODT instead of the usual approximation theoretical foundations, we formulate a very robust geometry and topology optimization of Bézier meshes based on a new simple functional promoting isotropic and uniform Jacobians throughout the domain. We demonstrate that our resulting curved meshes can adapt to complex domains with high precision even for a small count of elements thanks to the added flexibility afforded by more control points and higher order basis functions.
References:
1. Remi Abgrall, Cécile Dobrzynski, and Algiane Froehly. 2012. A method for computing curved 2D and 3D meshes via the linear elasticity analogy: preliminary results. Technical Report RR-8061. INRIA. https://hal.inria.fr/hal-00728850Google Scholar
2. Pierre Alliez, David Cohen-Steiner, Mariette Yvinec, and Mathieu Desbrun. 2005. Variational tetrahedral meshing. In ACM Trans. Graph., Vol. 24. ACM, 617–625. Google ScholarDigital Library
3. Pierre Alliez, Nathalie Laurent, Henry Sanson, and Francis Schmitt. 1999. Mesh approximation using a volume-based metric. In Pacific Conf. on Computer Graphics and Applications. 292–301. Google ScholarDigital Library
4. Nina Amenta, Marshall Bern, and David Eppstein. 1999. Optimal Point Placement for Mesh Smoothing. J. Algorithms 30, 2 (1999), 302–322. Google ScholarDigital Library
5. Ivo Babuska, Barna Szabo, and Norman Katz. 1981. The p-version of the Finite Element Method. SIAM J. Num. Anal. 18, 3 (1981), 515–545.Google ScholarCross Ref
6. Adam W. Bargteil and Elaine Cohen. 2014. Animation of Deformable Bodies with Quadratic Bézier Finite Elements. ACM Trans. Graph. 33, 3 (June 2014), Art. 27. Google ScholarDigital Library
7. Jean-Daniel Boissonnat, David Cohen-Steiner, and Mariette Yvinec. 2006. Comparison of algorithms for anisotropic meshing and adaptive refinement. Tech. Rep. ACS-TR-362603, INRIA (2006).Google Scholar
8. Max Budninskiy, Beibei Liu, Fernando de Goes, Yiying Tong, Pierre Alliez, and Mathieu Desbrun. 2016. Optimal Voronoi Tessellations with Hessian-based Anisotropy. ACM Trans. Graph. 35, 6, Article 242 (2016). Google ScholarDigital Library
9. David Cardoze, Alexandre Cunha, Gary L. Miller, Todd Phillips, and Noel Walkington. 2004. A Bézier-based Approach to Unstructured Moving Meshes. In Symp. Computat. Geom. 310–319. Google ScholarDigital Library
10. Isaac Chao, Ulrich Pinkall, Patrick Sanan, and Peter Schröder. 2010. A Simple Geometric Model for Elastic Deformations. ACM Trans. Graph. 29, 4, Article 38 (2010). Google ScholarDigital Library
11. Long Chen. 2004. Mesh Smoothing Schemes based on Optimal Delaunay Triangulations. In Int. Meshing Roundtable. 109–120.Google Scholar
12. Long Chen and Michael Holst. 2011. Efficient mesh optimization schemes based on optimal Delaunay triangulations. Computer Methods in Applied Mechanics and Engineering 200, 9 (2011), 967–984.Google ScholarCross Ref
13. Long Chen and Jin-chao Xu. 2004. Optimal delaunay triangulations. J. Computational Mathematics (2004), 299–308.Google Scholar
14. Zhonggui Chen, Wenping Wang, Bruno Lévy, Ligang Liu, and Feng Sun. 2014. Revisiting Optimal Delaunay Triangulation for 3D Graded Mesh Generation. SIAM J. Sci. Comput. 36, 3 (2014), 930–954.Google ScholarCross Ref
15. Siu-Wing Cheng, Tamal K. Dey, Herbert Edelsbrunner, Michael A. Facello, and Shang-Hua Teng. 2000. Sliver Exudation. J. ACM 47, 5 (2000), 883–904. Google ScholarDigital Library
16. Siu-Wing Cheng, Tamal K. Dey, and Jonathan R. Shewchuk. 2012. Delaunay Mesh Generation. CRC Press. Google ScholarDigital Library
17. Tony D. DeRose. 1988. Composing Bézier Simplexes. ACM Trans. Graph. 7, 3 (July 1988), 198–221. Google ScholarDigital Library
18. Qiang Du, Vance Faber, and Max Gunzburger. 1999. Centroidal Voronoi tesselations. SIAM Rev. 41, 4 (1999), 637–676. Google ScholarDigital Library
19. Lori A. Freitag and Carl Ollivier-Gooch. 1997. Tetrahedral Mesh Improvement using Swapping and Smoothing. Int. J. Numer. Meth. Engng. 40, 21 (1997), 3979–4002.Google ScholarCross Ref
20. Xiao-Ming Fu, Yang Liu, John Snyder, and Baining Guo. 2014. Anisotropic Simplicial Meshing Using Local Convex Functions. ACM Trans. Graph. 33, 6 (2014), Art. 182. Google ScholarDigital Library
21. Zhanheng Gao, Zeyun Yu, and Michael Holst. 2012. Quality Tetrahedral Mesh Smoothing via Boundary-optimized Delaunay Triangulation. Comput. Aided Geom. Design 29, 9 (2012), 707–721. Google ScholarDigital Library
22. Abel Gargallo-Peiró, Xevi Roca, Jaimie Peraire, and Josep Sarrate. 2013. High-order mesh generation on CAD geometries. In Int. Conf. on Adaptive Modeling & Simulation. 301–312.Google Scholar
23. Christophe Geuzaine, Amaury Johnen, Jonathan Lambrechts, Jean-Fraçois Remacle, and Thomas Toulorge. 2015. The Generation of Valid Curvilinear Meshes. In Notes on Numerical Fluid Mechanics and Multidisciplinary Design, Vol. 128. 15–39.Google ScholarCross Ref
24. Gaël Guennebaud, Benoît Jacob, and others. 2018. Eigen v3. http://eigen.tuxfamily.org. (2018).Google Scholar
25. Amaury Johnen, Jean-François Remacle, and Christophe Geuzaine. 2013. Geometrical validity of curvilinear finite elements. J. Comp. Phys. 233, Supplement C (2013), 359–372. Google ScholarDigital Library
26. Steve L. Karman, J. T. Erwin, Ryan S. Glasby, and Douglas Stefanski. 2016. High-Order Mesh Curving Using WCN Mesh Optimization. In 46th AIAA Fluid Dynamics Conference.Google Scholar
27. Patrick M. Knupp. 2001. Algebraic Mesh Quality Metrics. SIAM J. Sci. Comput. 23, 1 (2001), 193–218. Google ScholarDigital Library
28. Yang Liu, Wenping Wang, Bruno Lévy, Feng Sun, Dong-Ming Yan, Lin Lu, and Chenglei Yang. 2009. On Centroidal Voronoi Tessellation – Energy Smoothness and Fast Computation. ACM Trans. Graph. 28, 4 (2009), Art. 101. Google ScholarDigital Library
29. Adrien Loseille and Frédéric Alauzet. 2009. Optimal 3D Highly Anisotropic Mesh Adaptation Based on the Continuous Mesh Framework. In Int. Meshing Roundtable. 575–594.Google Scholar
30. Xiao-Juan Luo, Mark S. Shephard, Jean-Francois Remacle, Robert M. OBara, Mark W. Beall, Barna Szabo, and Ricardo Actis. 2002. p-Version Mesh Generation Issues. In Int. Mesh Roundtable. 343–354.Google Scholar
31. Mark Meyer, Mathieu Desbrun, Peter Schröder, and Alan H. Barr. 2003. Discrete Differential-Geometry Operators for Triangulated 2-Manifolds. 35–57.Google Scholar
32. Johannes Mezger, Bernhard Thomaszewski, Simon Pabst, and Wolfgang Straßer. 2008. Interactive Physically-based Shape Editing. In Symp. Solid Phys. Modeling. 79–89. Google ScholarDigital Library
33. Edmond Nadler. 1986. Piecewise linear best L2 approximation on triangulations. In Approx. Theory V, C. K. Chui et al. (Ed.). Academic Press, 499–502.Google Scholar
34. Ray W. Ogden. 1997. Non-linear Elastic Deformations. Dover Publications.Google Scholar
35. Per-Olof Persson and Jaime Peraire. 2009. Curved Mesh Generation and Mesh Refinement using Lagrangian Solid Mechanics.Google Scholar
36. Elisabeth Pilgerstorfer and Bert Jüttler. 2014. Bounding the influence of domain parameterization and knot spacing on numerical stability in Isogeometric Analysis. Comput. Methods in Appl. Mech. Eng. 268, Supplement C (2014), 589–613.Google ScholarCross Ref
37. Ulrich Pinkall and Konrad Polthier. 1993. Computing Discrete Minimal Surfaces and Their Conjugates. Experimental Mathematics 2, 1 (1993), 15–36.Google ScholarCross Ref
38. Helmut Pottmann and Michael Hofer. 2003. Geometry of the squared distance function to curves and surfaces. In Visualization and mathematics III. Springer, 221–242.Google Scholar
39. Laurent Rineau and Mariette Yvinec. 2008. Meshing 3D Domains Bounded by Piecewise Smooth Surfaces. 443–460.Google Scholar
40. Samuel Roth, Markus Gross, Silvio Turello, and Friedrich Carls. 1998. A Bernstein-Bézier Based Approach to Soft Tissue Simulation. Computer Graphics Forum 17, 3 (1998), 285–294.Google ScholarCross Ref
41. Eloi Ruiz-Girones, Abel Gargallo-Peiró, Josep Sarrate, and Xevi Roca. 2017. An augmented Lagrangian formulation to impose boundary conditions for distortion based mesh moving and curving. In Int. Meshing Roundtable.Google Scholar
42. Nico Schlömer. 2018. Numerical integration (quadrature, cubature) in Python. (2018). https://github.com/nschloe/quadpyGoogle Scholar
43. Jonathan R. Shewchuk. 1998. Tetrahedral Mesh Generation by Delaunay Refinement. In Symp. on Comp. Geometry. 86–95. Google ScholarDigital Library
44. Jonathan R. Shewchuk. 2002. What is a Good Linear Element? Interpolation, Conditioning, and Quality Measures. In Int. Meshing Roundtable. 115–126.Google Scholar
45. Stefan Suwelack, Dimitar Lukarski, Vincent Heuveline, Rüdiger Dillmann, and Stefanie Speidel. 2013. Accurate Surface Embedding for Higher Order Finite Elements. In Symp. Comp. Anim. 187–192. Google ScholarDigital Library
46. The CGAL Project. 2017. CGAL User and Reference Manual (4.11 ed.). CGAL Editorial Board, http://doc.cgal.org/4-11/Manual/packages.htmlGoogle Scholar
47. Jane Tournois, Camille Wormser, Pierre Alliez, and Mathieu Desbrun. 2009. Interleaving Delaunay refinement and optimization for practical isotropic tetrahedron mesh generation. ACM Trans. Graph. 28, 3 (2009), Art-No. Google ScholarDigital Library
48. Daniel Weber, Thomas Kalbe, André Stork, Dieter Fellner, and Michael Goesele. 2011. Interactive deformable models with quadratic bases in Bernstein-Bézier-form. The Visual Computer 27, 6 (2011), 473–483. Google ScholarDigital Library
49. Freddie D. Witherden and Peter E. Vincent. 2015. On the identification of symmetric quadrature rules for finite element methods. Comp. & Math. Appl. 69, 10 (2015), 1232–1241. Google ScholarDigital Library
50. Verena Ziel, Hadrien Bériot, Onur Atak, and Génaël Gabard. 2017. Comparison of 2D curving methods with modal shape functions and a piecewise linear target mesh. In Int. Meshing Roundtable.Google Scholar